Unraveling the Physics of Nanometer-Scale Fluidic Phenomena at the Single-Molecule Level

Francesco Fornasiero (13-ERD-030)

Abstract

Carbon nanotubes hold the potential to provide superior platforms for elucidating novel, poorly understood nanometer-scale fluidic phenomena. To advance the understanding of fluid behavior under nanoscale confinement, we developed a novel, ideal platform for fundamental molecular transport studies, in which the fluidic channel is a single carbon nanotube (CNT). These CNTs offer the advantage of simple chemistry and structure, which can be synthetically tuned with nanometer precision and accurately modeled. With combined experimental and computational approaches, we demonstrated that CNT pores with 1- to 5-nm diameters conduct giant ionic currents that follow an unusual sub-linear electrolyte concentration dependence. The large magnitude of the ionic conductance appears to originate from a strong electroosmotic flow in smooth CNT pores. First-principle simulations suggest that electroosmotic flow arises from localized negative polarization charges on carbon atoms near a potassium ion and from the strong cation–graphitic wall interactions, which drive potassium ions much closer to the wall than chlorides. Single-molecule translocation studies reveal that charged molecules may be distinguished from neutral species on the basis of the sign of the transient current change during their passage through the nanopore. Along with shedding light on a few controversial questions in the CNT nanofluidics area, these results may provide the foundation for development of an advanced single-molecule detection system for biological, chemical, or explosive analytes. In addition, these experimental and computational platforms can be applied to advance fundamental knowledge in other fields, from energy storage and membrane separation to superfluid physics.

Background and Research Objectives

When fluids are confined in nanoscale structures approaching the fluid physical length scale, novel physical phenomena are observed, many of which remain poorly understood. Advancing their understanding is critical for their future exploitation in high-performance devices that could provide a groundbreaking step forward in applications such as ultrasensitive detection systems,¹ nanoporous energy storage and harvesting platforms,^2–4 and separation systems.⁵ Methods that allow for a direct investigation of ions and single molecule motion in well-defined nanopores and their direct comparison with simulation predictions are critical for a rapid development of the field. Nanopore analytics enable a label-free, direct investigation of the passage of ions and of a single-molecule through nanopores. However, previous approaches based on biological and solid-state nanopores failed to provide the required pore size control at the nanoscale, simple chemistry and geometry, robustness, and the ability of local chemical functionalization in the same fluidic platform.¹ As revealed by molecular dynamics simulations, ionic transport through nanopores is sensitive even to minute changes in the structure of the same chemical composition.⁶

We proposed to advance the fundamental understanding of transport phenomena in confined nanoscale geometries by a synergistic experimental and theoretical investigation of ionic and molecular transport in an ideal, model nanopore. To this end, we developed a novel nanofluidic platform that is an advanced Coulter counter with a single CNT with a 1- to 5-nm diameter as the flow channel. We chose CNTs as nanopores because of their superior properties for nanopore analytics and their simple structure that is known with atomic precision, thus enabling accurate modeling.¹

At the same time, we planned to synergistically employ a multiscale computational framework (first principle plus classical molecular dynamics plus continuum) for modeling transport through a CNT and to provide unique insights into microscopic mechanisms governing nanoscale transport. Classical molecular dynamics simulations have been used in the past to predict a number of surprising features for fluid transport in narrow CNTs, such as ultrafast fluid flow,^7–9 transport rates independent of CNT length,¹⁰ spontaneous water filling,⁷ and DNA insertion.¹¹ However, only a few of these interesting predictions have been validated experimentally because of the lack of adequate nanofluidic platforms. Moreover, most of the existing molecular dynamics studies of fluid flow in CNTs have relied on rather simple water models that are fit to reproduce known bulk liquid properties. As such, their applicability to complex interfacial systems characteristic of a fluid-filled CNT is questionable.^12,13 Because we adopted a multiscale approach, potentials used in our simulations provide a more accurate description of fluid properties in confined nanoscale structures.

Together with the development of an experimental nanofluidic platform, specific objectives of this work include: (1) quantifying the magnitude of electric-field–driven ionic transport in CNTs, identifying primary charge carriers, and understanding which transport mode dictates the giant ion conductance claimed to be sustained by these nanochannels; (2) demonstrating detection of nanometer-sized molecules; and (3) unraveling the relationship between chemical and physical properties of the analytes and their molecular transport under confinement. The first two objectives were demonstrated, and we made substantial progress on the third by addressing an open question in the literature regarding the sign of the current modulation during single-molecule translocation.

Scientific Approach and Accomplishments

Experiments

The solid-state nanofluidic devices were fabricated following the steps in Figure 1. We first produced 3- to 10-mm, vertically aligned CNT forests by chemical vapor deposition and then infiltrated the CNTs with a low-pressure silicon-nitride deposition. After forming a window on the back side of silicon chip, focused-ion-beam nanometer-scale machining was used to open a single CNT for fluid transport on one surface of the aligned CNT silicon-nitride thin film, whereas all CNTs were opened using reactive ion etching on the other surface. Measurements of ion current with voltage and in time were performed in potassium-chloride solutions with two silver and silver-chloride electrodes using the Axopatch 200B and 1550 Digidata system (Molecular Devices, Inc.). Data analysis was performed with Clampfit 10.4 and Origin 9.0.

Figure 1. Micro-fabrication steps of the nanometer-scale fluidic devices. Scanning electron microscopic images for steps 2–5 show cross sections of the device region enclosed by the dashed red square at that specific fabrication step. (1) Deposition of an ~30-nm aluminum-oxide barrier layer and a catalyst layer of 5.5-Å iron and 0.5-Å molybdenum onto a silicon wafer. (2) Top: growth of vertically aligned carbon nanotubes (CNTs) by chemical vapor deposition. Below: vertically aligned CNT array. (3) Top: conformal low-pressure chemical vapor deposition of silicon-nitride deposition to fill the gaps between the nanotubes. Below: silicon-nitride and CNT composite with a silicon-nitride overlayer. (4) Top: potassium hydroxide etching to form 250-nm thick silicon-nitride window, and focused-ion-beam sculpting of a >20-nm hole on the silicon-nitride and aluminum-oxide layer to open one (or a few) of the CNT tips on the patterned side of the membrane. Below: nanopore drilled by a focused ion beam (FIB). (5) Top: removal of excess silicon nitride and opening of all nanotubes by reactive ion etching (RIE) on the opposite side of the membrane. Below: etched top-surface of the silicon-nitride and CNT composite showing exposed nanotube tips.

Multiscale Simulations

First-principles and classical molecular dynamics simulations were carried out to investigate the structure of potassium-chloride solution under confinement. The simulation setup consists of 1.0-M concentration salt solution with the bulk water density inside a 1.4-nm-diameter (19,0) CNT. Interatomic forces were derived from density functional theory in first-principles simulations, while nonpolarizable and polarizable empirical force fields were employed in classical simulations. To understand the effect of the interaction between potassium ion and carbon diffusive pi orbitals on the structure of the solution, we also considered polarizable force fields with and without the inclusion of cation–pi interaction.

Ionic conductances in nanopore structures mimicking the actual nanofluidic devices were calculated by numerically solving a coupled Poisson equation, a Nernst–Planck equation, and Navier–Stokes equations using the COMSOL Multiphysics 4.3 package, with and without slip boundary conditions at the CNT inner wall.

Results

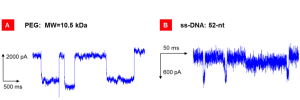
We first demonstrated the successful fabrication of the nanofluidic device by providing evidence of transport through a single CNT pore. This included the recording of a significant (nano-amp range) potassium-chloride ionic current only after the last pore-opening step, and the detection of transient current blockades with a single current level after introducing a small particle with size comparable to the CNT diameter (Figure 2).
 

Once we validated the nanofluidic platform, we addressed open questions about ionic conductance in CNTs. Several molecular dynamics studies have been published about ionic transport driven by an electric field through a single CNT, but only a few initial experimental investigations with conflicting results have been reported.¹⁴ While Strano et al. suggest stochastic pore blocking by the cations (potassium and sodium) in solution and hydron and hydroxide as primary charge carriers,^15,16 other reports did not observe current blockades for potassium-chloride solutions.^17,18 Moreover, Lindsay et al. indicated a possibility of a strongly enhanced potassium-chloride transport by electroosmosis,^17,19 whereas others measured conductivities in CNT similar to bulk values.¹⁸ To unravel the physics behind electric-field–driven ion transport in CNTs, we thoroughly investigated the current-voltage characteristics of the CNT channel as a function of the solution concentration, pH, and field strength.²⁰

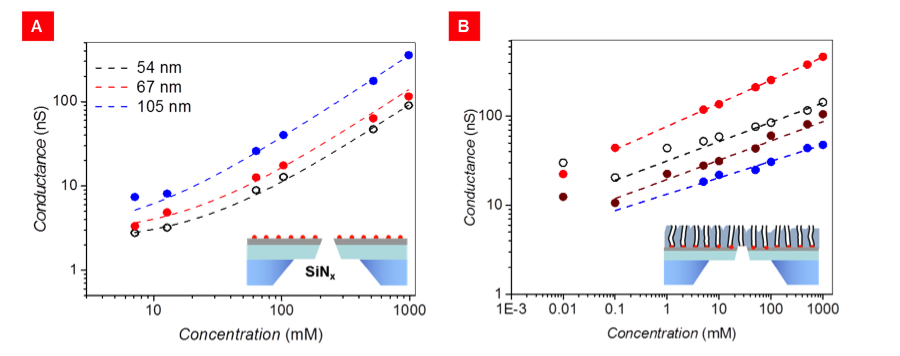
These tests revealed that:(1) ionic conductance is weakly dependent on solution pH, thus excluding protons as primary charge carriers; (2) ionic conductance in CNT pores is orders of magnitude larger than expected on the basis of the pore dimensions and bulk conductivities, as shown in Figure 3; (3) this giant conductance follows an unusual, sub-linear power-law dependence on potassium-chloride concentration, as shown in Figure 3(B), with an exponent in the range of 0.18 to 0.26, in agreement with the finding from Lindsay’s group;^17,19 and (4) reference devices without CNTs (i.e., a focused-ion-beam pore in a silicon-nitride film) show the expected magnitude and concentration dependence of potassium-chloride conductivity.

Figure 3. Ionic conductance dependence on concentration. (A) Reference devices with a single nanopore nano-machined with a focused ion beam in the silicon-nitride and alumina layer (no carbon nanotubes) display a classical conductance behavior: conductance is linearly increasing with electrolyte concentration at high molarity and reaches a plateau at low concentrations. (B) Carbon nanotube channels show anomalous ionic conductance, with a magnitude exceeding predictions based on pore size and bulk conductivity by orders of magnitude and with a sub-linear power-law dependence on electrolyte concentration C at all molarities (G ~ Cⁿ, n = 0.18–0.26).

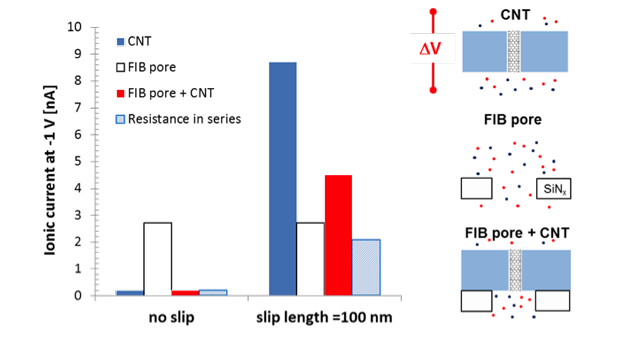
Published worked attributed the enormous potassium-chloride conductance to large electroosmotic flow, which stems from the negative charge and the large slip at the CNT walls.¹⁹ However, the origin of this charge remains unclear and no direct evidence of electroosmostic flow was given. Comparison of our data in Figure 3 reveals that devices with CNTs in series with the focused-ion-beam pore (of ~54-nm diameter) have conductance comparable or even larger than the reference devices with only a focused-ion-beam pore with the same diameter, which is in apparent contradiction with the resistance-in-series model prediction. This unexpected result can be explained with a large electroosmotic flow in CNTs and CNT-containing platforms. Electroosmotic enhancement of ionic transport is negligible in the reference devices lacking nanotubes, and is not accounted for by the traditional resistance-in-series models. Thus, our experiments provide strong evidence that electroosmotic flow is dominant in CNTs. To further validate this claim, we performed continuum calculation and quantified ionic conductance for a single focused-ion-beam pore, a charged 4-nm CNT with and without slip, and a focused-ion-beam pore and charged CNT with and without slip. Results confirmed that, for sufficiently large slip lengths and with a charged CNT wall, the system combining both focused ion beam and CNT pores can sustain currents that are comparable or larger than those of the reference focused-ion-beam pore, as shown in Figure 4.

Figure 4. Ionic current at V = −1 V for a charged (1 e/nm²), 4-nm-diameter carbon nanotube (CNT) pore with and without slip (dark blue); a neutral, 30-nm-diameter focused-ion-beam (FIB) pore drilled in a 280-nm silicon-nitride membrane (white); the focused-ion-beam pore and CNT pore in series (red); and predicted by the resistance-in-series model (light blue).

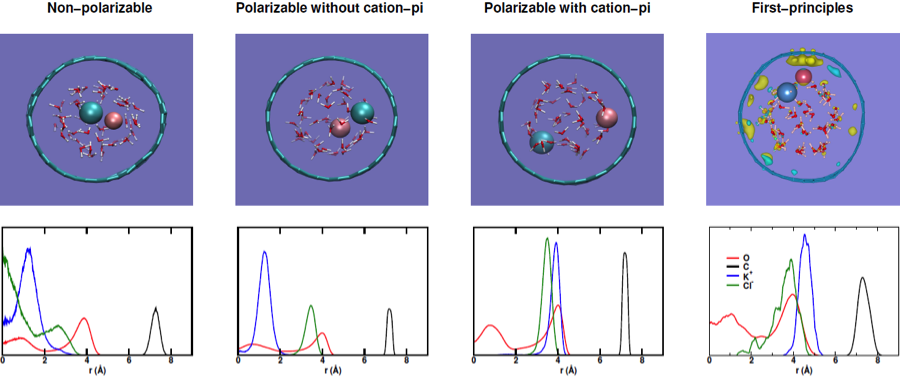
Clues on the mechanistic origin of this electroosmotic flow were obtained with first-principle simulations. The radial distribution function of potassium-chloride solution in a CNT (Figure 5) shows the propensity of both ions to reside near the interface with the potassium cations being noticeably closer to the CNT wall. The radial density distribution of potassium cations is rather narrow and indicates strong interaction between these cations and the CNT wall, as well as the tendency of the ions to be desolvated. In addition, the electronic density difference extracted from the molecular dynamics trajectory shown in Figure 5 reveals the formation of localized negative polarization charges on carbon atoms near the ions, which reinforces the interaction between the CNT and the ions. These interfacial effects in confined pores, particularly the charge rearrangement at the interface, may explain the origin of electroosmotic flow in CNTs. Note also, that typical force fields used in classical molecular dynamics simulations cannot capture correctly the ion structure in CNT pores, and that the inclusion of polarizability and cation–pi interactions is critical to obtaining a structure of the potassium-chloride solution in qualitative agreement with first-principles simulations.²¹

Figure 5. First-principle and classical molecular dynamics predictions of the structure of potassium-chloride solution inside a 14-Å single-walled carbon nanotube. From left to right: classical molecular dynamics with non-polarizable, polarizable, polarizable + cation–pi force field, and first-principle molecular dynamics simulations. Top row: snapshots of the molecular dynamics trajectories; light blue = chloride; violet = potassium cation; red = oxygen; white= hydrogen. Negative and positive polarization charges on the carbon nanotube are represented by the yellow and blue surfaces, respectively. Bottom row: radial distribution functions for water (oxygen), potassium cation, and chloride.

After investigating ionic transport in CNTs, we turned our attention toward single-molecule translocation in these nanochannels. A recent publication¹⁷ experimentally validated the molecular dynamics prediction that oligonucleotide strands can translocate through narrow CNT nanochannels.²² In this work, DNA translocation events were associated to unusual positive current spikes, and the underlying physics remains poorly understood. To elucidate single-molecule transport events in a nanofluidic channel, we considered single-molecule translocation for charged (ss-DNA) and neutral analytes (PEG) as shown in Figure 2. Our experiments revealed that, while neutral-molecule translocation transiently blocked the ionic flow of the supporting electrolyte as expected, an ionic current increase (spike) was recorded with negatively charged ss-DNA. Tests performed with smaller negatively charged dyes gave qualitative similar results. While unusual, a transient current enhancement may occur when the counter ions accompanying a translocating charged molecule dominate over the steric blockage effect, thus resulting in a greater number of current-carrying ions inside the pore.^23–26 The markedly different signals we recorded for charged or neutral molecules support this explanation.

Impact on Mission

This project furthered the Laboratory’s core competency in bioscience and bioengineering by providing design criteria for ultrasensitive detection systems and for chemical and biological protective membranes, and furthered the energy security mission by improving energy harvesting and separation. This work provided the fundamental science for development of an advanced single-molecule detection system for biological, chemical, or explosive analytes. Our efforts in advanced functional nanometer-scale materials also support LLNL’s core competency in advanced materials and manufacturing.

Conclusion

We developed a novel nanofluidic platform for the investigation of ionic and molecular transport in a model, robust nanochannel with tunable dimensions. The chosen nanochannel (a CNT) can be accurately modeled thanks to its simple chemistry and structure. With nanopore analytics techniques, we demonstrated giant ionic conductances in these pores that follow an anomalous power-law concentration dependence. Synergistic molecular dynamic and continuum simulations revealed that this large conductance is likely caused by a strong electroosmotic flow, which is due to the formation of localized negative polarization charges on the CNT walls near potassium cations. The latter tend to be stationed very close to graphitic walls because of cation–pi interactions. Single-molecule translocations studies support the idea that the passage of charged molecules through a nanochannel can produce current spikes, whereas neutral-molecule transport induces the expected current blockades. Thus, charged and uncharged molecules can be distinguished on the basis of the shape of the ionic current recording. Future work will be directed toward examining the potential of the platform for detection of molecules differing by other chemico-physical properties. The developed platform will be also employed for fundamental understanding of confinement effects on super-capacitor performance and for cutting-edge studies of superfluid transport.

References

1. Howorka, S., and Z. Siwy, "Nanopore analytics: Sensing of single molecules." Chem. Soc. Rev. 38(8), 2360 (2009).
2. Daiguji, H., et al., "Electrochemomechanical energy conversion in nanofluidic channels." Nano Lett. 4(12), 2315 (2004).
3. Chmiola, J., et al., "Anomalous increase in carbon capacitance at pore sizes less than 1 nanometer." Science 313(5794), 1760 (2006).
4. van der Heyden, F. H. J., et al., "Power generation by pressure-driven transport of ions in nanofluidic channels." Nano Lett. 7(4), 1022 (2007).
5. Fornasiero, F., et al., "Ion exclusion by sub-2-nm carbon nanotube pores." Proc. Natl. Acad. Sci. Unit. States Am. 105(45), 17250 (2008).
6. Cruz-Chu, E. R., A. Aksimentiev, and K. Schulten, "Ionic current rectification through silica nanopores." J. Phys. Chem. C 113(5), 1850 (2009).
7. Hummer, G., J. C. Rasaiah, and J. P. Noworyta, "Water conduction through the hydrophobic channel of a carbon nanotube." Nature 414(6860), 188 (2001).
8. Skoulidas, A. I., et al., "Rapid transport of gases in carbon nanotubes." Phys. Rev. Lett. 89(18), 4 (2002).
9. Dellago, C., M. M. Naor, and G. Hummer, "Proton transport through water-filled carbon nanotubes." Phys. Rev. Lett. 90(10), 4 (2003).
10. Kalra, A., S. Garde, and G. Hummer, "Osmotic water transport through carbon nanotube membranes." Proc. Natl. Acad. Sci. Unit. States Am. 100(18), 10175 (2003).
11. Gao, H. J., et al., "Spontaneous insertion of DNA oligonucleotides into carbon nanotubes." Nano Lett. 3(4), 471 (2003).
12. Cicero, G., et al., "Water confined in nanotubes and between graphene sheets: A first principle study." J. Am. Chem. Soc. 130(6), 1871 (2008).
13. Huang, P., E. Schwegler, and G. Galli, "Water confined in carbon nanotubes: Magnetic response and proton chemical shieldings." J. Phys. Chem. C 113(20), 8696 (2009).
14. Guo, S., et al., "Nanofluidic transport through isolated carbon nanotube channels: Advances, controversies, and challenges." Adv. Mater. 27(38), 5726 (2015).
15. Lee, C. Y., et al., "Coherence resonance in a single-walled carbon nanotube ion channel." Science 329(5997), 1320 (2010).
16. Choi, W., et al., "Diameter-dependent ion transport through the interior of isolated single-walled carbon nanotubes." Nat. Comm. 4 (2013).
17. Liu, H. T., et al., "Translocation of single-stranded DNA through single-walled carbon nanotubes." Science 327(5961), 64 (2010).
18. Geng, J., et al., "Stochastic transport through carbon nanotubes in lipid bilayers and live cell membranes." Nature 514(7524), 612 (2014).
19. Pang, P., et al., "Origin of giant ionic currents in carbon nanotube channels." ACS Nano 5(9), 7277 (2011).
20. Guo, S., et al., Anomalous ionic conductance in narrow-diameter carbon nanotube pores. (2015).
21. Pham, T. A., et al., Ab-initio simulation of KCl solution in carbon nanotubes: The role of cation-pi Interaction. (2015).
22. Yeh, I. C., and G. Hummer, "Nucleic acid transport through carbon nanotube membranes." Proc. Natl. Acad. Sci. Unit. States Am. 101(33), 12177 (2004).
23. Smeets, R. M. M., et al., "Salt dependence of ion transport and DNA translocation through solid-state nanopores." Nano Lett. 6(1), 89 (2006).
24. Kowalczyk, S. W., and C. Dekker, "Measurement of the docking time of a DNA molecule onto a solid-state nanopore." Nano Lett. 12(8), 4159 (2012).
25. Vlassarev, D. M., and J. A. Golovchenko, "Trapping DNA near a solid-state nanopore." Biophys. J. 103(2), 352 (2012).
26. Venta, K. E., et al., "Gold nanorod translocations and charge measurement through solid-state nanopores." Nano Lett. 14(9), 5358 (2014).

Publications and Presentations

• Buchsbaum, S. F., et al., Giant conductance and anomalous concentration dependence in sub-5 nm carbon nanotube nanochannels. Molecular Foundry User Mtg., Berkeley, CA, Aug. 20–21, 2015. LLNL-POST-676398-DRAFT.
• Bui, N., et al., Carbon nanotube nanofluidics: From fundamental to applied science. 2014 Materials Research Society Fall Mtg., Boston, MA, Nov. 30–Dec. 5, 2014. LLNL-PRES-664525.
• Bui, N., et al., Transport in carbon nanotube nanochannels under different driving forces. Royal Society Theo Murphy Mtg., Newport Pagnell, UK, Apr. 27, 2015. –LLNL-ABS-665307.
• Guo, S., et al., Anomalous ionic conductivity in sub-5 nm carbon nanotube nanochannels. 2015 Materials Research Society Spring Mtg., San Francisco, CA, Apr. 6–10, 2015. LLNL-ABS-663162.
• Guo, S., et al., A simple, single-carbon-nanotube nanofluidic platform for fundamental transport studies. 2014 Materials Research Society Spring Mtg., San Francisco, CA, Apr. 21–25, 2014. LLNL-PRES-653667.
• Guo, S., et al., A simple, single-carbon-nanotube nanofluidic platform for fundamental transport studies. Biophysical Society Mtg., San Francisco, CA, Feb. 15–19, 2014. LLNL-POST-649578.
• Guo, S., et al., Carbon nanotubes as nanofluidic channels. 2015 Materials Research Society Spring Mtg., San Francisco, CA, Apr. 6–10, 2015. LLNL-POST-668915.
• Guo, S., et al., Giant conductance and anomalous concentration dependence in sub-5 nm carbon nanotube nanochannels. Biophysical Society 59th Mtg., Baltimore, MA, Feb. 7–11, 2015. LLNL-POST-666854.
• Guo, S., et al., "Nanofluidic transport through isolated carbon nanotube channels: Advances, controversies, and challenges." Adv. Mater. 27(38), 5726 (2015). LLNL-JRNL-666424.