Randolph Hood (13-ERD-067)
Abstract
The current challenge in condensed matter and chemical physics for development of a predictive foundation for materials on demand is the accurate solution of the Schrödinger equation, which describes how the quantum state of a physical system changes with time. Despite decades of effort, there are still major difficulties in predicting and explaining many phenomena. Density functional theory has been the standard electronic structure method used in first-principles simulations. Although this theory provides reasonable predictions at modest computational costs, its accuracy is eventually limited by its approximate treatment of electron correlation. With the advent of petascale computing, we are able to move beyond density functional theory, which is a method of obtaining an approximate solution to the Schrödinger equation of a many-body system, and employ accurate many-body quantum Monte Carlo, with its favorable scaling and its inherent ability to yield systematically improved results. Monte Carlo algorithms rely on repeated random sampling to compute their results. We performed benchmark calculations of the fundamental electronic properties of selected materials across the periodic table using state-of-the-art quantum Monte Carlo. Our objective was to establish the power of the quantum Monte Carlo method by demonstrating the level of accuracy achievable for materials properties associated with both equation of state and energy applications such as excited-state properties including band gaps. We calculated the equation of state of five transition metals, sodium chloride, and tin, and the band gaps of five different materials. We performed calculations of solid cerium and plutonium. Obtaining this data was essential for establishing the fidelity of the method, demonstrating its applicability to mission-relevant applications, and allowing us to determine areas where quantum Monte Carlo required further development, notably the optimal choice of pseudopotentials, which are used as approximations for the simplified description of complex systems. The calculations were performed using a Livermore Computing Grand Challenge and five Capability Computing Campaign awards. The approaches we developed are now being utilized in calculations of new materials in a project funded by the DOE Basic Energy Sciences, and has positioned us to pursue additional support.
Background and Research Objectives
The current challenge in condensed matter and chemical physics, and the most significant bottleneck in the development of a predictive theory foundation for materials on demand, is the accurate solution of the many-body Schrödinger equation. Despite decades of effort invested in its solution by one-particle, mean-field, and perturbative methods, there are still major difficulties in predicting and explaining many phenomena related to bonding, cohesion, optical properties, conductivity, and other quantum effects. Over the last two decades, density functional theory has been the standard electronic structure method used in first-principles simulations. Although density functional theory provides reasonable predictions at modest computational costs, its accuracy is eventually limited by its approximate treatment of electron correlation. Current implementations of density functional theory suffer from the following major limitations: (1) excited-state properties such as optical gaps and spectra are generally unreliable; (2) serious deficiencies in describing van der Waals interactions (which are the residual attractive or repulsive forces between molecules or atomic groups that do not arise from a covalent bond, or electrostatic interaction of ions or of ionic groups with one another or with neutral molecules), nonequilibrium geometries such as reaction barriers, systems with transition metals, or cluster isomers with competing bonding patterns; (3) significant errors occur when treating strongly correlated materials; and (4) problems describing small band-gap materials (especially relevant for solar applications).
It is clear that to advance the field of first-principles simulations, we need more-accurate electronic structure methods, ones that have a built-in way of assessing the accuracy of the calculation to establish benchmarks for density functional theory functionals. With the advent of petascale computing, we are finally in a position to move beyond mean-field treatments such as density functional theory and employ more accurate many-body approaches. Given the strength of the algorithm, its favorable scaling properties, and its inherent ability to obtain systematically improved results, we strongly believe that quantum Monte Carlo will play a leading role in the future of electronic structure calculations for condensed matter.
For this project, we planned to perform gold-standard benchmark calculations of the fundamental electronic properties of selected materials across the periodic table using state-of-the-art quantum Monte Carlo. Our objective was to establish the power of the quantum Monte Carlo method by demonstrating the level of accuracy achievable for materials properties associated with both equation of state (lattice constants, phase stability, and bulk modulus) and energy applications such as excited-state properties including band gaps and band alignment. Obtaining this data was essential for both establishing the fidelity of the method, and most importantly, allowing us to pinpoint the areas where quantum Monte Carlo still required development. Determining the conditions under which current best practices in quantum Monte Carlo succeed and fail on these systems laid the groundwork for the second phase of this work in which we extended the method to the treatment of actinides, materials notoriously difficult to treat accurately with theory yet play an increasingly strategic role in both technology and national security. What follows is a summary of our objectives and what was completed for each.
Objective 1: Test and apply existing quantum Monte Carlo code base to compute equation-of-state properties of the solids molybdenum, tantalum, palladium, rhodium, silver, sodium chloride, indium arsenide, and tin. Assess the effects of nodal errors and choice of pseudopotentials on one or more of these systems. For one or more systems, determine phase stability at high pressure predicted by quantum Monte Carlo.
Completed: Performed equation-of-state calculations of molybdenum, tantalum, palladium, rhodium, silver, sodium chloride, and tin. Assessed effects of nodal errors in molybdenum, palladium, and silver, and choice of pseudopotentials in palladium, rhodium, silver, and tin. Determined phase stability of tin at high pressure.
Objective 2: Carry out extensive calculations of band gaps and spectral data of the solids sodium chloride, magnesium hydride, silicon carbide, gallium phosphide, and indium phosphide. Assess the effects of nodal errors and choice of pseudopotentials on one or more of these systems.
Completed: Computed band gaps and spectral data of sodium chloride, magnesium hydride, silicon carbide, gallium phosphide, and indium phosphide. Assessed the effects of nodal errors and choice of pseudopotentials in silicon carbide.
Objective 3: Carry out quantum Monte Carlo calculations of equation-of-state properties of one or more lanthanides and actinides.
Completed: Computed equations of state for cerium and plutonium.
In addition to these objectives, we carried out extensive quantum Monte Carlo calculations of molecular dimers (often formed by the reaction of two identical compounds) to assess effectiveness of pseudopotentials for solid-state quantum Monte Carlo calculations.
Scientific Approach and Accomplishments
The quantum Monte Carlo algorithm we used for our calculations was a fixed-node diffusion Monte Carlo.1 This is a stochastic method for evolving a wave function using the imaginary-time, fully interacting many-body Schrödinger equation. This first-principles approach offers high accuracy and excellent scaling. It also can be applied to systems containing thousands of electrons and has near perfect parallelization on petascale-sized computers. In principle, and in contrast to most electronic structure methods, systematic errors can be measured and systematically reduced.2,3 In practice, the most significant sources of error are (1) the fixed-node and fixed-phase approximations, a variational solution to the Fermion sign problem; (2) finite-size effects, which, in contrast to insulators, are a significant problem in metals; and (3) pseudopotential error and corresponding locality error.
The fixed-node or fixed-phase is obtained from the guiding wave function. This function is a product of Slater determinants for up- and down-spin electrons (a Slater determinant is an expression that describes the wave function of a multi-fermionic system that satisfies anti-symmetry requirements, and consequently the Pauli principle, by changing sign upon exchange of two electrons) and a Jastrow correlation function (the Jastrow factor is the primary method for including electron correlation beyond the mean-field level in quantum Monte Carlo simulations). The single-particle orbitals in the determinants were obtained from density functional theory calculations using the plane-wave PWscf code (Plane-Wave Self-Consistent Field).4 To improve the efficiency of the calculations, we evaluated the orbitals in quantum Monte Carlo via real-space cubic splines.5 Parameters in the Jastrow function were optimized by minimizing the variance of energy.6 In systems where improved nodes were required, we included backflow in our guiding wave functions.7 For our quantum Monte Carlo calculations, we used the CASINO code, which is capable of calculating accurate solutions to the Schrödinger equation of quantum mechanics for realistic systems built from atoms.8
Calculations of solids using quantum Monte Carlo require finite super-cells with periodic boundary conditions imposed on the Hamiltonian. This leads to finite-size effects that were treated using twist-averaged boundary conditions on the guiding wave functions, along with either extrapolation to infinite-sized super-cells by repeating calculations with different-sized cells or by including a correction with density functional theory using post-quantum Monte Carlo.9,10
An important consideration in simulating materials with quantum Monte Carlo is the separation of energy scales between core and valence electrons. The electrons that are tightly bound to nuclei in the core of an atom do not directly contribute to the physics relevant in materials, except via the Pauli exclusion principle. Calculations using pseudopotentials developed with density functional theory have been successful for many systems.
Equation-of-State Properties
The equation of state at zero temperature for a crystalline solid relates the energy or pressure to the atomic volume. This can be determined directly by performing total-energy ground-state quantum-Monte-Carlo calculations at a range of atomic volumes and fitting the quantum Monte Carlo data to an equation of state such as developed by Murnaghan, which reflects material behavior under a pressure range as wide as possible to connote the experimentally established fact that the more a solid is compressed, the more difficult it is to compress further.11 From this equation of state, one can deduce the quantum Monte Carlo equilibrium-lattice constant, the bulk modulus, and the cohesive energy. Repeating this procedure for the solid in different crystalline phases yields relative phase stability, which can be used to predict low-temperature phase transitions.
Table 1 compares our calculated equation of state using quantum Monte Carlo and density functional theory. The results show that quantum Monte Carlo yields better equation-of-state parameters than density functional theory when compared with experiment. The density functional theory results are shown using the Perdew–Burke–Ernzerhof exchange-correlation functional.12 For these solids, the mean absolute error of quantum Monte Carlo from experiment is significantly smaller compared to density functional theory using the Perdew–Burke–Ernzerhof functional. The quantum Monte Carlo results for the first derivative of bulk modulus agreed with experiment for all systems within the statistical error bars (one sigma uncertainty) associated with the stochastic nature of quantum Monte Carlo, as shown in parentheses. We also calculated the equation-of-state properties of plutonium and cerium.
Table 1. Parameters obtained from a fit to the Murnaghan equation of state from quantum Monte Carlo (QMC) or density functional (DFT) theory compared with experiment (EXP). The numbers in parenthesis for QMC data correspond to one-sigma statistical error bars. The finite-temperature and zero-point energy contributions have been removed from the experimental data for the five transition metals. The mean absolute error (Error) compared with experiment is also shown.
| Lattice Parameter (atomic units) | Bulk Modulus (Mbar) | Derivative Bulk Modulus | |||||||
| DFT | QMC | EXP | DFT | QMC | EXP | DFT | QMC | EXP | |
| Silver | 7.827 | 7.73(1) | 7.690 | 0.91 | 0.98(4) | 1.057 | 5.5 | 5(1) | 4.73 |
| Palladium | 7.438 | 7.305(4) | 7.325 | 1.71 | 1.95(4) | 1.872 | 5.6 | 5.4(3) | 5 |
| Rhodium | 7.228 | 7.111(3) | 7.155 | 2.60 | 2.91(4) | 2.771 | 4.7 | 5.0(3) | 4.5 |
| Tantalum | 6.287 | 6.250(3) | 6.232 | 1.91 | 1.80(6) | 2.027 | 3.4 | 4.1(5) | 3.75 |
| Molybdenum | 5.989 | 5.917(2) | 5.938 | 2.53 | 2.75(1) | 2.76 | 4.0 | 4.1(1) | 3.98 |
| Sodium chloride | 5.697 | 5.63(2) | 5.634 | 31 | 32(3) | 25.9 | 3.6 | 2(3) | 4.54 |
| Tin (diamond phase) | 6.631 | 6.47(2) | 6.477 | 36 | 53(5) | 53 | 4.9 | 4(3) | 4 |
| Tin (beta phase) | -- | 5.795(8) | 5.831 | -- | 66(3) | 57.9 | -- | 6.1(8) | -- |
| Tin (bct phase) | 3.999 | 3.931(2) | 3.891 | 43 | 51.7(3) | 52.0 | 4.5 | 4.77(8) | -- |
| Error | 1.54% | 0.43% | -- | 14.0% | 7.35% | -- | 12.3% | 13.3% | -- |
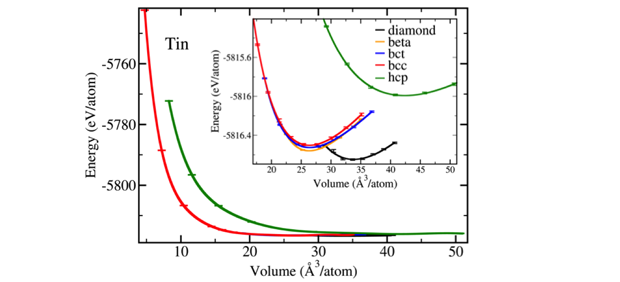
We computed the quantum Monte Carlo equation of state for tin for several different phases (see Figure 1). The optimal axial ratio for the beta, body-centered-tetragonal, and hexagonal-close-packed phases was determined using density functional theory. The corresponding transition pressures computed from quantum Monte Carlo are shown in Table 2. The pressures derived from quantum Monte Carlo agree closely with experiment. There is a large difference between the body-centered-cubic to hexagonal-close-packed transition pressure computed using density functional theory versus quantum Monte Carlo. While most density functional theory studies predict body centered cubic to transform to hexagonal close packed at 160 to 200 GPa, quantum Monte Carlo shows no transition up to 1,954 GPa. A recent experimental study did not observe a transition up to 1,200 GPa.13
Table 2. Transition pressures (gigapascals) between different phases of tin: diamond, beta, body-centered-tetragonal (bct), body-centered-cubic (bcc), and hexagonal-close-packed (hcp) phases. Calculations performed using density functional theory (DFT) and quantum Monte Carlo (QMC) were compared with experimental results.
| Tin | diamond → beta (GPa) | beta → bct (GPa) | bct → bcc (GPa) | bcc → hcp (GPa) |
| DFT | 0.2 (Ref. 14) 0.7 (Ref. 15) 1.9 (Ref. 16) 0.15 (Ref. 17) 0.75 (Ref. 18) |
10.4 (Ref. 14) 12 (Ref. 15) 13 (Ref. 16) 2.7 (Ref. 17) |
50 (Ref. 14) 45 (Ref. 15) 32 (Ref. 16) 28 (Ref. 17) |
160 (Ref. 15) No transition up to 200 (Ref. 16) 163 (Ref. 18) |
| QMC | 1.9 | 13 | 41 | No transition up to 1,954 |
| Experiment | 0 (Ref. 19) | 9.8 (Ref. 19) 10 (Ref. 20) 9.7 (Ref. 21) 15.9 (Ref. 18) |
35 (Ref. 20) 40 (Ref. 21) 42.9 (Ref. 18) |
No transition up to 1,200 (Ref. 22) |
Among the possible systematic errors (fixed-node error, finite-size effects, and choice of pseudopotential) present in our quantum Monte Carlo calculations, we found that the errors associated with using pseudopotentials had the largest impact on our calculated equation-of-state properties of solids. We determined several guiding principles for constructing pseudopotentials that yielded small errors in quantum Monte Carlo calculations:
- Quantum Monte Carlo calculations using the pseudopotential should be able to reproduce the ionization energy and electron affinity of an isolated atom.
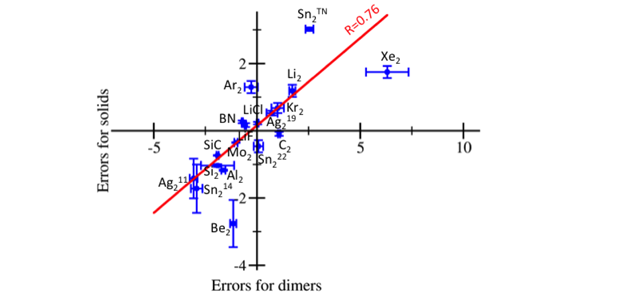
- The quality of quantum Monte Carlo calculations of dimers had a strong correlation with the quality of calculations of corresponding solids. Figure 2 illustrates this correlation in the quantum Monte Carlo errors of the equilibrium atomic spacing found in solids and in corresponding dimers. Therefore, small-scale quantum Monte Carlo calculations of atoms and dimers can be used to determine a promising pseudopotential before carrying out large-scale calculations of solids.
- Quantum Monte Carlo errors can be reduced by minimizing the overlap between the core and valence charge density, which may necessitate the inclusion of semi-core states in the valence.
- The errors associated with the locality approximation can be minimized by constructing pseudopotentials with similar angular momentum channels.
Band Gaps and Spectral Data
Although quantum Monte Carlo methods were originally designed to study ground states, they can also provide information about excited states. Excitation energies can be obtained by devising a many-electron guiding wave function that models an excited state. With the fixed-node constraint, the energy converges to the lowest energy consistent with the nodal surface, not to the ground state. Computing excitations in solids is computationally demanding because the relevant energy differences scale as 1/N, where N is the number of electrons in the super-cell. We computed band gaps and spectral data for solid magnesium hydride, the ionically bonded solid sodium chloride, and the covalent semiconductors silicon carbide, gallium phosphide, and indium phosphide.
In Table 3 we show the results of our quantum Monte Carlo calculations of the gaps for sodium chloride and magnesium hydride compared with experiment. The band gap was computed by combining separate ground-state energies of each system containing N, N + 1, and N − 1 electrons. Promoting an electron from the valence band to the conduction band and computing the energy difference of this excitation energy and the ground-state energy yields the optical or quasiparticle gap. In sodium chloride, which has a direct gap, the promotion was from an electron at the gamma point, while in magnesium hydride, which has an indirect gap, the promotion was from an electron at the Z point to the A point. Finite-size effects were treated in three different ways, with two using Ewald, a geometric construct used in electron, neutron, and x-ray crystallography to demonstrate the relationship between the wave-vector of the incident and diffracted x-ray beams, the diffraction angle for a given reflection, and the reciprocal lattice of the crystal. Our three treatments were as follows: (1) using Ewald for the Coulomb interaction with twist-averaging and extrapolating to infinity from calculations using different sized super-cells, (2) using Ewald with twist-averaging at one super-cell size and adding a correction based on density functional theory,10 and (3) using the model-pair Coulomb interaction.24,25 Table 3 shows that our quantum Monte Carlo results are in close agreement with experimental results. Our calculations of the gaps in silicon carbide, gallium phosphide, and indium phosphide disagree from experiment by more than 1 eV. We are testing the dependence of those results on the quality of the nodes.
Table 3. Calculated optical and band gaps of sodium chloride (NaCl) and magnesium hydride (MgH2) compared with experimental results. Calculations were performed with quantum Monte Carlo using the Ewald construct with extrapolation, Ewald with a correction based on density functional theory (KZK), and the model-pair Coulomb interaction (MPC). The numbers in parentheses for calculated data correspond to one-sigma statistical error bars.
| Electronvolts | NaCl Direct Gap Gamma → Gamma |
MgH2 Indirect Gap Z → A | ||
| Optical Gap | Band Gap | Optical Gap | Band Gap | |
| Ewald with extrapolation | 7.8(4) | 8.6(7) | -- | 6.8(5) |
| Ewald + KZK | -- | 8.4(7) | -- | 6.2(4) |
| MPC | 7.9(1) | 8.9(2) | 5.62(7) | 5.93(7) |
| Experiment | 7.92 (Ref. 26) | 8.97 (Ref. 26) | 5.6 (Ref. 27) 5.8 (Ref. 28) 6.05 (Ref. 29) |
|
Impact on Mission
Developing a core competency in advanced materials and manufacturing at LLNL by validating quantum Monte Carlo as a high-fidelity approach and enhancing its accuracy where necessary by computing equation of state and determining excited-state data for a broad range of materials impacts many national and energy security programs. Equation-of-state models form the core of theoretical high-energy-density science and stockpile stewardship science at the Laboratory, particularly for actinides. Quantum Monte Carlo can also be used for band gap engineering in the development of cost-effective detectors for radiation detection and discrimination for use in nuclear threat reduction and to develop improved solar electricity generation for renewable energy applications.
Conclusion
We performed “best practices” benchmark calculations using quantum Monte Carlo of ground- and excited-state properties of a greatly expanded range of materials than has been studied heretofore. This work enabled us to validate where current implementations of quantum Monte Carlo succeed and to pinpoint where improvements in quantum Monte Carlo methods were necessary. For elements with high atomic numbers, we determined that the largest systematic errors in quantum Monte Carlo arise from the choice of the pseudopotential. We identified the characteristics that a pseudopotential should satisfy to minimize its associated errors, allowing us to obtain excellent agreement in calculations of equation-of-state properties of solids. The approaches we developed were transitioned to calculations of programmatically relevant materials and to a project funded by the DOE Basic Energy Sciences.
References
- Foulkes, W. M., et al., “Quantum Monte Carlo simulations of solids.” Rev. Mod. Phys. 73(1), 33 (2001).
- Umrigar, C. J., et al., “Alleviation of the fermion-sign problem by optimization of many-body wave functions.” Phys. Rev. Lett. 98, 110201 (2007).
- Bajdich, M., et al., “Systematic reduction of sign errors in many-body calculations of atoms and molecules.” Phys. Rev. Lett. 104, 193001 (2010).
- Giannozzi, P., et al., “QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials.” J. Phys. Condens. Matter 21, 395502 (2009).
- Williamson, A. J., R. Q. Hood, and J. C. Grossman, “Linear-scaling quantum Monte Carlo.” Phys. Rev. Lett. 87, 246406 (2001).
- Umrigar, C. J., K. G. Wilson, and J. W. Wilkins, “Optimized trial wave functions for quantum Monte Carlo calculations.” Phys. Rev. Lett. 60, 1719 (1988).
- López-Ríos, P., et al., “Inhomogeneous backflow transformations in quantum Monte Carlo.” Phys. Rev. E 74, 066701 (2006).
- Needs, R. J., et al., “Continuum variational and diffusion quantum Monte Carlo calculations.” J. Phys. Condens. Matter 22, 023201 (2010).
- Lin, C., F. H. Zong, and D. M. Ceperley, “Twist-averaged boundary conditions in continuum quantum Monte Carlo algorithms,” Phys. Rev. E 64, 016702 (2001).
- Kwee, H., S. Zhang, and H. Krakauer, “Finite-size correction in many-body electronic structure calculations.” Phys. Rev. Lett. 100, 126404 (2008).
- Murnaghan, F. D., “The compressibility of media under extreme pressures.” Proc. Natl. Acad. Sci. Unit. States Am. 30(9), 244 (1944).
- Perdew, J. P., K. Burke, and M. Ernzerhof, "Generalized gradient approximation made simple." Phys. Rev. Lett. 77, 3865 (1996).
- Trail, J. R., and R. J. Needs, “Norm-conserving Hartree–Fock pseudopotentials.” J. Chem. Phys. 122, 014112 (2005).
- Lazicki, A., et al., “X-ray diffraction of solid tin to 1.2 TPa.” Phys. Rev. Lett. 115, 075502 (2015).
- Christensen, N. E., and M. Methfessel, “Density-functional calculations of the structural properties of tin under pressure.” Phys. Rev. B 48, 5797 (1993).
- Yu, C., et al., “Ab initio calculation of the properties and pressure induced transition of Sn.” Solid State Comm. 140(11–12), 538 (2006).
- Cui, S., et al., “First-principles study of phase transition of tin and lead under high pressure.” Phys. Status Solidi B 245(1), 53 (2008).
- Mukherjee, D., K. D. Joshi, and S. C. Gupta, “Pressure induced phase transition in tin: Ab-initio calculations.” J. Phys. Conf. 215(1), 012106 (2010).
- Olijnyk, H., and W. Holzaplfel, “Phase transitions in Si, Ge and Sn under pressure.” J. Phys. Colloq. 45 (C8), C8-153 (1984).
- Trail, J. R., and R. J. Needs, “Smooth relativistic Hartree-Fock pseudopotentials for H to Ba and Lu to Hg.” J. Chem. Phys. 122, 174109 (2005).
- Liu, M., and L. Liu, “Compressions and phase transitions of tin to half a megabar.” High Temp. High Press. 18, 79 (1986).
- Fraser, L. M., et al., “Finite-size effects and Coulomb interactions in quantum Monte Carlo calculations for homogeneous systems with periodic boundary conditions.” Phys. Rev. B 53, 1814 (1996).
- Williamson, A. J., et al., “Elimination of Coulomb finite-size effects in quantum many-body simulations.” Phys. Rev. B 55, R4851 (1997).
- Roessler, D. M., and W. C. Walker, “Electronic spectra of crystalline NaCl and KCl.” Phys. Rev. 166, 599 (1968).
- Isidorsson, J., et al., “Optical properties of MgH2 measured in situ by ellipsometry and spectrophotometry.” Phys. Rev. B 68, 115112 (2003).
- He, Z. X., and W. Pong, “X-ray photoelectron spectra of MgH2.” Phys. Scripta 41(6), 930 (1990).
- Yamamoto, K., et al., “Optical transmission of magnesium hydride thin film with characteristic nanostructure,” J. Alloy. Comp. 330–332, 352 (2002).
Publications and Presentations
- Nazarov, R., R. Hood, and M. Morales, Accurate band gaps of semiconductors and insulators from quantum Monte Carlo calculations. American Physical Society Mtg., San Antonio, TX, Mar. 2–6, 2015. LLNL-PRES-667789.
- Nazarov, R., R. Hood, and M. Morales, Accurate diffusion Monte Carlo calculations of the properties of molecules, metals and insulators. Psi-K Conf., San Sebastian, Spain, Sept. 6–10, 2015. LLNL-POST-676683.
- Nazarov, R., R. Hood, and M. Morales, Benchmarking DMC for molecules, metals and insulators: Nonlocal pseudopotentials challenge. TSRC Workshop on Stochastic Methods in Electronic Structure Theory, Telluride, CO, June 8–12, 2015. LLNL-POST-672064.
- Nazarov, R., et al., Quantum Monte Carlo calculations of phase transitions in Sn. MRS Mtg., Boston, MA, Nov. 30–Dec. 5, 2014. LLNL-POST-664756.