Wyatt Du Frane (15-LW-067)
Abstract
Everything we know about the inside of Earth is derived from remote surface measurements in combination with modeling and experiments. Because of the high temperatures of the Earth's mantle, we have no way of drilling deeper than Earth's crust. We proposed to determine the relationship of hydrogen diffusion and conduction in upper-mantle minerals as a tool for inferring hydrogen distribution in the mantle. Nominally anhydrous minerals formed deep in the mantle and transported to the Earth’s surface have been found to contain tens to hundreds of parts per million by weight of water, providing evidence for its presence in the Earth’s interior. Even at these low concentrations, water greatly affects the physico-chemical properties of mantle materials, governing planetary dynamics and evolution. The diffusion of hydrogen controls the transport of water in the upper mantle, but is not fully understood for olivine, the most abundant mineral in this region. Hydrogen self-diffusion coefficients in natural olivine single crystals were determined at upper-mantle conditions (2 GPa and 750–900°C) to be highly anisotropic, with values at 900°C of 10-10.9, 10-12.8, and 10-11.9 m2/s along [100], [010], and [001] directions, respectively. From these diffusion results, we determined the contribution of hydrogen on olivine electrical conductivity via the Nernst–Einstein relation. Comparisons between the model presented in this study and magneto-telluric measurements suggest that olivine water contents comparable to those expected in the upper mantle (≤250 ppm weight) can account for high electrical conductivity values observed in the asthenosphere, the upper layer of the Earth's mantle, below the lithosphere.
Background and Research Objectives
Earth’s hydrosphere is a distinctive feature of our planet, where massive oceans affect its climate and support its ecosystem. The presence of water on Earth, however, is not limited to its outermost shell but extends to great depths within the planet. Downwelling oceanic lithosphere (at subduction zones), and upwelling magmas (at mid-ocean ridges, volcanoes, and hotspots) are vehicles for volatiles, such as water, to cycle deep into the Earth’s interior.1 Experimental studies have shown that it is possible for substantial amounts of water to be present in the mantle, hosted as defects in the structure of nominally anhydrous minerals. The major mineral component of the uppermost mantle, olivine, can incorporate as much as approximately 1-wt% water at conditions encountered at the lowest portion of the upper mantle.2 Minerals found in mantle xenoliths, including olivine, that are brought to surface by alkaline or kimberlitic magma eruptions, contain up to hundreds of parts per million by weight of water3 and provide direct evidence that water is present in the Earth’s interior. Recently, a crystal of terrestrial ringwoodite (a higher-pressure polymorph of olivine that forms below ~410-km depth) containing about 1.4-wt% water was discovered as an inclusion in a natural diamond,4 confirming that at least some regions within Earth’s transition zone contain large amounts of water.
Water, as hydrogen bonded to the crystal structure, has the potential to affect the physical and chemical properties of minerals,5 even if present at only several parts per million by weight. For example, hydrogen influences the rheological properties of minerals and has been proposed as a possible factor in weakening hydrogen-bearing olivine in the convective mantle, while relatively dry olivine is thought to stabilize the cratonic mantle.6 Also, hydrogen favors the formation of fluids and melts within the Earth by lowering the melting temperature of rocks,7 affecting the chemical differentiation of the planet. Therefore, understanding the presence and transport of hydrogen in the Earth’s mantle is crucial to understanding planetary evolution and global dynamics.
Because of the high sensitivity of electrical conductivity to hydrogen content, it can potentially be used as a geophysical tool for mapping water contents throughout the mantle, but the precise relationship is poorly constrained. High-pressure and high-temperature in situ experiments have been conducted to directly measure the electrical conductivity of olivine as a function of water content. Two recent studies reached contrasting conclusions on the electrical conductivity of hydrous olivine.8,9 Substantial follow-on work has been devoted to determining the influence of hydrogen on olivine and mantle conductivity,10 but the discrepancy among the published data sets remains unresolved.
Hydrogen self-diffusion in olivine provides an alternative method for determining electrical conductivity, while circumventing some of the experimental difficulties associated with in situ electrical conductivity measurements. The Nernst–Einstein relation can be used to relate generalized mobility of hydrogen to its electrical mobility.11 We produced the first hydrogen self-diffusion coefficients (DH) in single-crystal olivine for all three principal crystallographic orientations of olivine. The new results are used to model the effect of hydrogen on olivine electrical conductivity and reconcile some of the discrepancies in previously reported results. This diffusion-based model can be used to infer olivine water contents up to 250 ppm wt of water through comparison with electrical conductivity anomalies observed in the asthenosphere, which is comparable to the range in mid-ocean ridge basalts.
Scientific Approach and Accomplishments
We obtained results at 2 GPa and 750 to 900°C via hydrogen–deuterium exchange experiments coupled with nanoscale secondary-ion mass spectrometry analysis of the resulting isotopic profiles. Hydrogen diffusion profiles were successfully measured along [100], [010], and [001] directions of olivine crystals. We prepared the samples using a three-step procedure consisting of a dry anneal at high temperature, a wet anneal to saturate the samples with hydrogen at high pressure and temperature, and a final exchange anneal for the isotopic exchange at high pressure and temperature.12,13 In a recent multi-laboratory comparative study, sample PC28 was found to contain about 75-ppm-wt water,14 which is similar to samples from longer-duration experiments at similar conditions that are expected to be saturated by incorporation mechanism.15
The hydrogen–deuterium analytical profiles, quantified as 16O2H/28Si, begin at the edge and progress toward the center of the crystal, on a path perpendicular to the edge. We used high-resolution scanning electron microscopy to accurately determine the position of each nanoscale secondary-ion mass spectrometry crater (Figure 1). In all profiles, the hydrogen content decreased from the edge of the crystal toward the center. The hydrogen diffusion profiles in the [100] direction are much longer than those for [010] and [001] orientations (Figure 2). The 16O2H/28Si profiles (Figure 2) were fit to the solution to Fick’s second law of diffusion for a semi-infinite solid to obtain hydrogen self-diffusion coefficients, DH,[hkl], as a function of orientation,16 given in Miller indices, or [hkl].
Figure 1. Back-scattered electron image showing nanoscale secondary-ion mass spectrometry ion beam craters for the [001] profile on olivine experimental sample PC25.
Figure 2. Deuterium diffusion profiles for experimental sample PC25 (2 GPa, 750°C). Profiles show 16O2H normalized to 28Si as a function of distance normal to faces oriented along [100] (blue diamonds), [001] (red triangles), and [010] (yellow circles), with lines showing fits.
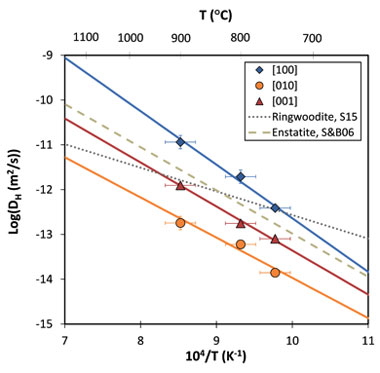
The temperature dependence of DH,[010] and DH,[001] were determined for the first time for olivine in this study. The DH,[010] and DH,[001] are 1 to 2 log units lower than DH,[100], which is consistent with hydrogen chemical diffusion coefficients reported for the reduction and oxidation exchange mechanism.17 The DH,[100], DH,[010] and DH,[001] all increase exponentially with temperature between 750 to 900°C, and were fit to the Arrhenius equation (Figure 3). The activation enthalpies (i.e., temperature dependence) are comparable to those of enstatite,18 and slightly higher than ringwoodite,19 suggesting a similar diffusion mechanism among different silicates (Figure 3). The magnitudes of the DH determined in this study suggest that mixed vacancy-interstitial diffusion in olivine is controlled by a dissociative mechanism,20 where an activated hydrogen dissociates from a magnesium vacancy and migrates as an interstitial particle until it is trapped again at another thermal vacancy.20
Figure 3. Arrhenius plot showing hydrogen self-diffusion coefficients as a function of inverse temperature. Solid lines represent weighted fits of the experimental data along the three different orientations. Dashed and dotted lines show hydrogen self-diffusion coefficients for enstatite and ringwoodite, respectively.
The new measurements of DH,[010] and DH,[001] complete the description of anisotropy for hydrogen self-diffusion in olivine as a function of temperature, which is critical for determining electrical conductivity of the mantle. The hydrogen self-diffusion coefficients are used to calculate the contribution of hydrogen to olivine electrical conductivity by applying the Nernst–Einstein relation, and combined with conductivity for dry olivine21 to determine the total conductivity of hydrated olivine.
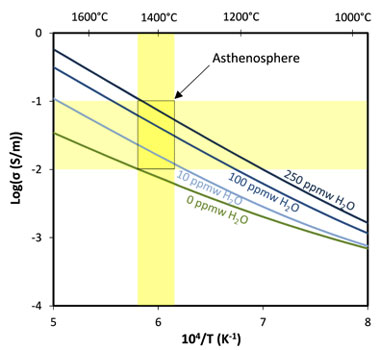
The electrical conductivity of the Earth’s mantle can be estimated using a geometric mean of the three principal orientations. The contribution of hydrogen was determined to be σH = 102.12 S/m • CH2O • exp−175 kJ/mol/(RT), where C is the concentration of water in ppm wt, and R is the gas constant. This approximation can be combined with any of the various models that have been published for electrical conductivity of nominally anhydrous olivine. The hydrogen-diffusion-based model compares favorably with the range of electrical conductivities values observed in the asthenosphere by magneto-telluric studies (Figure 4). Generally, this ranges between 10-1 S/m beneath continental lithosphere and 10-2 S/m beneath oceanic lithosphere.22 For depths of 120 to 240 km, roughly corresponding to where these anomalies are observed, pressure would be expected to increase from 4 to 8 GPa and temperature from 1,350 to 1,450°C based on adiabatic calculations.23 Olivine storage capacity would increase with depth from about 100 to 250 ppm wt based on these pressure and temperature conditions.24 The model in this study suggests that water contents below 250 ppm wt can account for most of the electrical conductivity anomalies observed by magneto-telluric soundings (Figure 4). Utilizing hydrogen partitioning parameterizations among upper-mantle mineral phases and predicted mineral abundances,25 the water content expected in olivine can be calculated for mantle assemblage with different overall water contents. The highest end of the range of mid-ocean-ridge basalt and ocean-island basalt mantle sources reported in the literature are approximately 200 and 1,000 ppm wt, respectively.26,27 For a mantle assemblage containing either 200- or 1,000-ppm-wt water at depths between about 120 and 240 km, the olivine would be predicted to contain 90- to 180-ppm-wt water and 470- to 900-ppm-wt water, respectively. The upper limit of 250-ppm-wt water inferred for olivine beneath oceanic lithosphere by this model therefore predicts mantle water contents that are close to those expected in mid-ocean-ridge basalt mantle sources, and well below ocean-island basalt mantle sources.
Figure 4. Hydrogen-diffusion-based model of olivine in comparison to geophysical measurements on Earth. Electrical conductivity is plotted as a function of inverse temperature and water (H2O) content. Yellow bands display electrical conductivity and temperature range of anomalies observed in the asthenosphere.
Impact on Mission
This work has extended our understanding of hydrogen diffusion and behavior of mantle materials and contributes to the knowledge base of materials science, especially under conditions of high pressure and temperature. This effort is relevant to the Laboratory's core competency in high-energy-density science, in which focused laboratory and computational experiments are recreating and characterizing conditions deep inside planets. In addition, our efforts may provide information on our climate, a delicate balance of complex systems, below, on, and above the Earth's surface, in support of the Laboratory's mission in energy and water security.
Conclusion
During this project, we produced the most comprehensive hydrogen self-diffusion data set to date. We used the results to develop a model for the electrical conductivity of hydrous olivine. Comparisons with geophysical observations from the upper mantle demonstrate that hydrogen self-diffusion coefficients are a promising tool for probing the presence of hydrogen in the Earth’s interior. Further investigation will allow the model to be used to map water contents regionally throughout the upper mantle. A deep-water cycle throughout Earth's history could explain why it has retained large bodies of water on its surface, unlike other nearby planetary bodies. The clearer snapshot of the current volatile distributions inside Earth in such an effort will give new insight on plate tectonics, planetary formation, and evolution. In addition to relevance to materials science, this research is expected to benefit understanding of our climate system, which depends on characterizing the flow of energy, water, and chemicals between the mantle, hydrosphere, and atmosphere. Furthermore, this project resulted in hiring a postdoctoral researcher and has led to successful, ongoing collaborations with Arizona State University and Cambridge University in the United Kingdom.
References
- Jacobsen, S. D., and S. Van der Lee, Earth’s deep water cycle. Geophysical Monograph Series, American Geophysical Union, Washington, DC (2006).
- Smyth, J. R., et al., "Olivine hydration in the deep upper mantle: Effects of temperature and silica activity." Res. Lett. 33, L15301 (2006). http://dx.doi.org/10.1029/2006GL026194
- Bell, D. R., and G. R. Rossman, "Water in Earth’s mantle: The role of nominally anhydrous minerals." Science 255, 1391 (1992).
- Pearson, D. G., et al., "Hydrous mantle transition zone indicated by ringwoodite included within diamond." Nature 507, 221 (2014).
- Bolfan-Casanova, N., "Water in the Earth’s mantle." Mineral. Mag. 69, 229 (2005). http://dx.doi.org/
- Peslier, A. H., et al., "Olivine water contents of the continental lithosphere and the longevity of cratons." Nature 467, 78 (2010).
- Kushiro, I., Y. Syono, and S-I. Akimoto, "Melting of a peridotite nodule at high pressures and high water pressures." Geophys. Res. 73, 6023 (1968). http://dx.doi.org/10.1029/JB073i018p06023
- Wang, D. J., et al., "The effect of water on the electrical conductivity of olivine." Nature 443, 977 (2006).
- Yoshino, T., et al., "Hydrous olivine unable to account for conductivity anomaly at the top of the asthenosphere." Nature 443, 973 (2006).
- Tyburczy, J. A., and W. L. Du Frane, "The electrical conductivity of rocks, minerals and the earth," Treatise on geophysics 2nd edition: Volume 2, mineral physics. Elsevier Ltd., Oxford, UK, G. Schubert, Series Ed. and L. Stixrude, Volume Ed. (2015).
- Karato, S., "The role of hydrogen in the electrical conductivity of the upper mantle." Nature 347, 272 (1990).
- Du Frane, W. L., and J. A. Tyburczy, "Deuterium–hydrogen exchange in olivine: Implications for point defects and electrical conductivity." Geophys. Geosys. 13, Q03004 (2012). http://dx.doi.org/10.1029/2011GC003895
- Novella, D., et al., "Hydrogen self-diffusion in olivine and electrical conductivity of the Earth’s mantle." Submitted to Scientific Reports, Nature Publishing Group, London, UK (2016).
- Ferris, E., et al., Secondary ion mass spectrometry (SIMS) measurements of hydrogen in olivine. Cooperative Institute for Deep Earth Research (CIDER) Workshop on Reconciling Laboratory Measurements on the Electrical Conductivity of Hydrous Olivine, Washington, DC, Aug. 22–23, 2016 (in preparation).
- Du Frane, W. L., et al., "Ringwoodite growth rates from olivine with ~75 ppm wt H2O: Metastable olivine must be nearly anhydrous to exist in the mantle transition zone." Earth Planet. Inter. 219, 1 (2013).
- Crank, J., The Mathematics of diffusion. Oxford University Press, Oxford, UK (1975).
- Kohlstedt, D. L., and S. J. Macwell, "Diffusion of hydrogen and intrinsic point defects in olivine." Phys. Chem. 207, 147 (1998).
- Stalder, R., and H. Behrens, "D/H exchange in pure and Cr-doped enstatite: Implications for hydrogen diffusivity." Chem. Mineral. 33, 601 (2006).
- Sun, W., et al., "Hydrogen self-diffusivity in single crystal ringwoodite: Implications for water content and distribution in the mantle transition zone." Res. Lett. 42, 6582 (2015). https://dx.doi.org/10.1002/2015GL064486
- Frank, F. C., and D. Turnbull, "Mechanism of diffusion of copper in germanium." Rev. 104, 617 (1956).
- Du Frane, W. L., et al., "Anisotropy of electrical conductivity in dry olivine." Res. Lett. 32, L24315 (2005). http://dx.doi.org/10.1029/2005GL023879
- Lizarralde, D., et al., "Northeastern Pacific mantle conductivity profile from long-period magnetotelluric sounding using Hawaii to California submarine cable data." Geophys. Res. 100, 17837 (1995). http://dx.doi.org/10.1029/95JB01244
- Katsura, T., et al., "Adiabatic temperature profile in the mantle." Earth Planet. Inter. 183, 212 (2010).
- Ardia, P., et al., "H2O storage capacity of olivine at 5–8 GPa and consequences for dehydration partial melting of the upper mantle." Earth Planet. Sci. Lett. 345, 104 (2012).
- Novella, D., et al., "The distribution of H2O between silicate melt and nominally anhydrous peridotite and the onset of hydrous melting in the deep upper mantle." Earth Planet. Sci. Lett. 400, 1 (2014).
- Bureau, H., et al., "A melt and fluid inclusion study of the gas phase at Piton de la Fournaire volcano (Réunion Island)." Geol. 147, 115 (1998).
- Saal, A. E., et al., "Vapour undersaturation in primitive mid-ocean-ridge basalt and the volatile content of Earth’s upper mantle." Nature 419, 451 (2002).
Publications and Presentations
- Du Frane, W. L., et al., "Electrical properties of methane hydrate + sediment mixtures." J. Geophys. Res. Solid Earth 120, 4773 (2015). LLNL-JRNL-653840. http://dx.doi.org/10.1002/2015JB011940
- Du Frane, W. L., et al., New hydrogen self diffusion coefficients in olivine using NanoSIMS. American Geophysical Union Fall Mtg., San Francisco, CA, Dec. 14–18, 2015. LLNL-ABS-675892.
- Du Frane, W. L., et al., Overview on hydrogen self diffusion and conduction in upper mantle minerals. (2016). LLNL-PRES-700960.
- Novella, D., et al., Accurate self-diffusion coefficients of hydrogen in olivine and implications for mantle electrical conductivity. Goldschmidt 2016, Yokohama, Japan, June 26–July 1, 2016. LLNL-PRES-695622.
- Novella, D., et al., Hydrogen self-diffusion in olivine and the electrical conductivity signature of the Earth's upper mantle. (2016). LLNL-POST-693757.
- Novella, D., et al., Investigating H (hydrogen) self-diffusion in olivine and upper mantle electrical conductivity. American Geophysical Union Fall Mtg., San Francisco, CA, Dec. 12–16, 2016. LLNL-POST-713857.


![15-lw-067_Fig2_380.jpg Figure 2. deuterium diffusion profiles for experimental sample pc25 (2 gpa, 750°c). profiles show <sup>16</sup>o<sup>2</sup>h normalized to <sup>28</sup>si as a function of distance normal to faces oriented along [100] (blue diamonds), [001] (red triangles), and [010] (yellow circles), with lines showing fits.](https://ldrd-annual.llnl.gov/sites/ldrd_annual/files/2020-10/15-lw-067_Fig2_380.jpg)
![15-lw-067_Fig1_380.jpg Figure 1. back-scattered electron image showing nanoscale secondary-ion mass spectrometry ion beam craters for the [001] profile on olivine experimental sample pc25.](https://ldrd-annual.llnl.gov/sites/ldrd_annual/files/2020-10/15-lw-067_Fig1_380.jpg)



