1. Home
  2. Report Archives
  3. FY2016
  4. High-Performance Computing, Simulation, and Data Science
  5. Numerical Performance and Parallel Scalability of Multi-Rate Integrators Based on Discrete-Event Simulation

Numerical Performance and Parallel Scalability of Multi-Rate Integrators Based on Discrete-Event Simulation

Carol Woodward (15-FS-014)

Abstract

The quantitative modeling and simulation of time-evolving natural and engineered systems entails numerically approximating solutions to sets of ordinary or partial differential equations by integrating in time. For many problems of practical interest, different components of the system evolve at different timescales. Examples of such problems occur in plasma physics, molecular dynamics, combustion chemistry, turbulence phenomena, and shock and stellar cluster evolution. To solve these kinds of problems efficiently while resolving relevant physics, one would ideally employ different time steps for different components of the system. To this end, multiple-rate methods were developed. In a fully multirate scheme, the integration is asynchronous in the sense that each component of the system evolves using its own time step. Creating a parallel scheme is challenging, because the different components are coupled and need to communicate while never residing at the same moment in simulation time. In our study, we investigated the feasibility of using parallel discrete-event simulation techniques for time integration of large-scale, multirate systems of ordinary differential equations of relevance to the DOE. Results indicated that the overhead of applying discrete event technologies can be very high, depending on the cost of evaluating problem physics. As a result, this technology will only be useful in very specific situations. In addition, the multirate integrator requires that information about the problem be provided by the application code in a way not used in single-rate integrators, resulting in the need for a careful user interface construction. Our main conclusion is that multirate integrators that can accommodate a limited number of step size partitions will likely give much more efficiency on these problems, and the discrete-event simulation-based method is only useful for highly multirate systems where a completely asynchronous method is required.

Background and Research Objectives

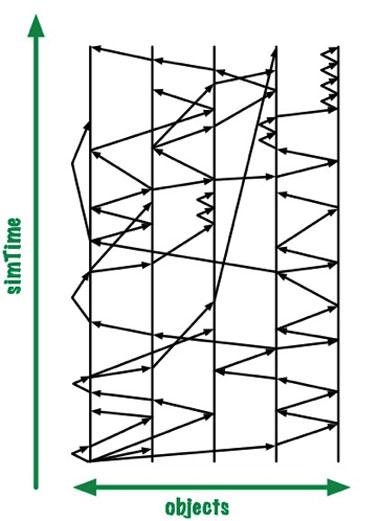
The quantitative modeling and simulation of time-evolving natural and engineered systems entails numerically approximating solutions to sets of ordinary or partial differential equations by integrating in time. For many problems of practical interest, different components of the system evolve at different time scales. To solve these kinds of problems efficiently while resolving relevant physics, one would ideally employ different timesteps for different components of the system. To this end, various multirate methods were developed.1–5 In a fully multirate scheme, the integration is asynchronous, in that each component of the system evolves using its own timestep (see Figure 1). Parallelizing such a scheme is challenging, since the different components are coupled and need to communicate while never residing at the same moment in simulation time. So far, little work has been done to realize a robust, general, and scalable parallel multirate integrator. Furthermore, most studies of multirate integration have been limited to problems with only a small number of time scales instead of a wide spectrum.

Figure 1. in a discrete-event simulation, updates of system state occur asynchronously through messages sent between variables.
Figure 1. In a discrete-event simulation, updates of system state occur asynchronously through messages sent between variables.

Our goal was to investigate the feasibility of a scalable, parallel, discrete-event simulation-based multirate integrator for ordinary differential equation systems of relevance to the DOE. Proposed work included the implementation of a massively parallel discrete-event simulation-based multirate integrator and tests on two classes of problems to study the numerical performance and scalability of the approach.

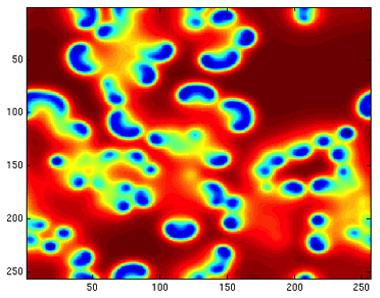
Our objectives were to implement Kofman's explicit, quantized state systems integrator under ROSS (Rensselaer's Optimistic Simulation System), a parallel discrete-event simulation code. Other objectives included studying the performance and robustness of this approach and, lastly, studying the numerical properties and performance of the method using two test problems: combustion and stellar cluster dynamics. Progress on these goals was limited due to the complexity of providing a way that would allow for efficient evaluation. In addition, developing specific test cases of the combustion problem proved to be more difficult than anticipated. As a result, we added a third test case, the Gray–Scott reaction–diffusion problem, in which reaction and diffusion of chemical species produce a variety of patterns, reminiscent of those often seen in nature, and used that for evaluation of method performance.

Scientific Approach and Accomplishments

We began by implementing the Euler-like quantized state systems method in ROSS frameworks for both discrete-event and non-discrete-event simulations, and testing it against problems such as a one-dimensional reaction–diffusion problem, a one-dimensional Allen-Cahn problem (which involves the process of phase separation in multi-component alloy systems, including order-disorder transitions), and a two-dimensional Gray–Scott problem (which involves modeling physical reactions). We also attempted to test the method using the Chemkin chemical combustion package, which is used for solving complex chemical kinetics problems. However adapting Chemkin to a discrete-event simulation framework proved to be far too time-consuming for the limited scope of our study.

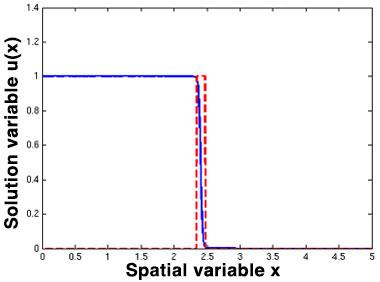
We targeted quantized state systems as it was the framework used in the only work we had identified as using discrete event technologies for continuous problems. The quantized state systems method determines timestep sizes, that is, it controls error, by determining when the change in each variable will exceed some fixed-size amount. As a result, variables always change in jumps of predetermined size, regardless of the size of error this change induces. This approach stands in contrast to the usual manner of step size selection, which is based on limiting temporal truncation error to be below a user-specified tolerance. Our tests showed that using fixed-size jumps had difficulties on problems with high-dynamic range, that is, problems where some variables change rapidly, but possibly in small amounts, while other variables change more slowly (see Figure 2). We decided to adapt a more traditional approach to error control in discrete-event simulation-based integrators and employed an explicit second-order Runge-Kutta method, which we have labeled as RK2 in this discussion. These one-step methods fit well with a discrete-event simulation-based approach, and error estimation is simple within the Runge-Kutta framework.

Figure 2. this graph represents the reaction-diffusion equation with burgers-like dynamics. the dynamic selection of fast variables is outlined in red for emphasis. over time, the shock-like front moves from left to right. the multi-rate method uses a fast step size within the red box, and a large step outside the red box where the solution is unchanging.
Figure 2. This graph represents the Reaction-Diffusion equation with Burgers-like dynamics. The dynamic selection of fast variables is outlined in red for emphasis. Over time, the shock-like front moves from left to right. The multi-rate method uses a fast step size within the red box, and a large step outside the red box where the solution is unchanging.

We compared the performance of the ROSS-based RK2 integrator against a variable time-step single-rate RK2 integrator, as well as a multirate non-discrete-event simulation implementation based on Savcenco time-stepping.5 The advantage of using a discrete-event simulation framework for multirate integration is that it provides a natural way to allow each variable to use step sizes tailored specifically to itself, which should minimize the number of steps taken. Due to the difficulty of managing each variable individually, non-discrete-event simulation multirate integrators generally group variables into rate classes. This grouping results in potentially significant inefficiencies due to the step size for any particular variable being the minimum over a large group of variables rather than for that variable alone. The tradeoff is that managing each variable individually adds additional overhead, which will be discussed below. The research question is whether managing each variable individually is worth the extra overhead, and where the cross-over point is between how many fewer time steps must be taken to justify the additional cost per step.

We first demonstrated that managing each variable individually can indeed significantly reduce the number of time steps needed to meet the requested tolerance. Table 1 shows the number of time steps needed, totaled over all variables (1 per variable, per step), by discrete-event simulation-based RK2, a variable step-size single-rate RK2, and a Savcenco time-stepped multirate RK2. The comparisons were made on a one-dimensional reaction–diffusion problem using 100 spatial points, a one-dimensional Allen–Cahn problem using 400 spatial points, and a two-dimensional Gray–Scott problem on a 256 x 256 grid (see Figure 3).8,9 The absolute error tolerance was 1e−6 for the one-dimensional problems and 1e−5 for the two-dimensional problem. Due to the additional interpolations necessary, the two multirate integrators were less accurate for the same tolerance as the single-rate integrator. But, the multirate methods had very similar accuracy between each other to the point that accuracy was not a difference in efficiency between them.

 

Table 1. Comparison of the number of time steps totaled over all variables.

  Time Stepping Algorithm
Problem Single-Rate Savcenco Discrete-Event Simulation
1D Reaction–Diffusion 1.4e7 1.1e6 3.2e4
1D Allen–Cahn 3.9e6 9.5e5 1.6e6
2D Gray–Scott 1.2e8 3.7e7 4.3e5
 
Figure 3. pattern formation in the gray–scott problem.
Figure 3. Pattern formation in the Gray–Scott problem.
 

We see that the fully asynchronous nature of the discrete-event simulation approach can result in fewer time steps compared with the semi-synchronous non-discrete-event simulation multirate approach. In particular, for the reaction–diffusion problem and the Gray–Scott problem, there were orders of magnitude of reductions in steps. On the other hand, for the Allen–Cahn problem, there was a mild reduction in the number of steps compared to the single-rate method, but the asynchronous method was no better than the Savcenco time-stepped method. Clearly the amount of reduction in time steps from an asynchronous integrator is problem dependent.

While a fully asynchronous discrete-event simulation-based approach can minimize the number of time steps needed, the overall efficiency is a balance between the number of time steps and the cost per step. In particular, the discrete-event simulation-based approach suffers from several sources of overhead not present in other integrators. First, there is an overhead to queueing the updates for each variable, and changes in variables must be explicitly communicated to neighbors through messages. Furthermore, since neighboring values are offset in time, the method must perform a large amount of interpolation and compute additional function evaluations each step. In Table 2, we list the central processing unit times for the tests of Table 1 when computed on a single processor.

 

Table 2. Comparison of central processing unit speed in seconds between the integrators.

  Time Stepping Algorithm
Problem Single-Rate Savcenco Discrete-Event Simulation
1D Reaction–Diffusion 1.6e-1 6.4e-1 3.7e-2
1D Allen–Cahn 4.0e-2 4.6e-2 1.8
2D Gray–Scott 2.5e1 1.3e1 2.7

For the reaction–diffusion problem and the Gray–Scott problem the central processing unit times for the discrete-event simulation-based method are less than for either the single-rate method or for the non-discrete-event simulation multirate method. While the method is overall the fastest, the time cost per step is clearly much higher than for the other two methods. For example, for the reaction-diffusion problem, the cost per step of the single-rate method is 1.1e-8 seconds. For the Savcenco multirate method, the cost is 5.8e-7 seconds per step, over an order of magnitude larger. For the discrete-event simulation-based method, the cost is 1.2e-6 seconds per step, which is an order of magnitude larger still. The balance is similar for the Gray–Scott problem. Clearly the problem needs to be sufficiently multirate to allow order of magnitude reductions in the number of steps before the discrete-event simulation-based method becomes worthwhile.

For problems for which the variables evolve similarly, the discrete-event simulation-based multirate method will not be worthwhile. An example of this is the Allen–Cahn problem, which only exhibited a minor reduction in the number of steps. As a result, both the parallel and non-parallel discrete-event simulation multirate integrators were more expensive than the single-rate integrator. However, the parallel discrete-event simulation-based method was far costlier than the other multirate method, exceeding it in cost by nearly two orders of magnitude.

We also developed a parallel stellar cluster dynamics test code, in which point masses influence each other by gravity and evolve according to Newton’s equations of motion. We implemented a forward Euler integration scheme, in parallel, using either a fixed single rate global timestep or a fully multirate integrator in which a timestep is chosen for each point mass independently of all other point masses. We observed that by accepting an error in evaluating the right-hand side of the ordinary differential equation, we could significantly reduce the amount of communication required by the method. We also demonstrated that this scheme is convergent and has the same global error properties as the normal multi-rate scheme.

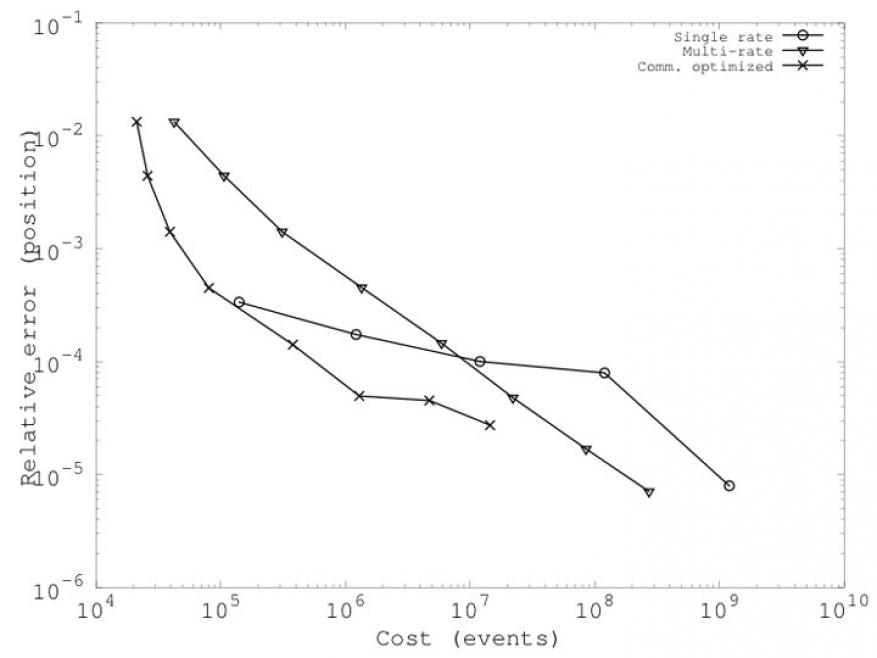
Figure 4 shows the cost of error in terms of number of events for the multirate parallel discrete-event simulation-based integrator compared to a single rate integrator for the stellar cluster dynamics problem. We see that reducing the communication, or number of events, is crucial for parallel performance. Without this reduction, speedup could not be achieved with the multirate integrator. Employing the communication reducing scheme, we could increase speed by as much as a factor of four in the parallel simulation.


Figure 4. relative error plotted as a function of the number of events (cost) for a single rate integrator compared with a parallel discrete-event simulation-based multirate integrator with and without communication optimizations.
Figure 4. Relative error plotted as a function of the number of events (cost) for a single rate integrator compared with a parallel discrete-event simulation-based multirate integrator with and without communication optimizations.
 

Impact on Mission

By providing scalable simulations of systems characterized by a wide spectrum of timescales, parallel discrete-event integrators could enable multiphysics simulations of ever-increasing realism and codes for efficient use of next-generation supercomputers, thus supporting the Laboratory's core competency in high-performance computing, simulation, and data science. We evaluated certain parallel discrete-event simulation-based integrators to determine whether they could support continuous mechanisms, which are key features of many realistic models. These integrators were found to be less efficient than continuous multirate methods. Thus, this work did not change any program directions. However, based on this study’s results, it was decided we should pursue research into continuous multirate methods that would allow for efficiency gains from a moderate number of step-size groups, as opposed to the fully asynchronous approach that discrete-event simulations require.

Conclusion

The use of a fully asynchronous multirate integrator can significantly reduce the number of time steps needed on problems with sufficient differences in time rates in the problem. However, the use of the parallel discrete-event simulation framework adds a large extra cost per step. In our tests, this cost was increased by about an order of magnitude per step compared to a more traditional multirate method, and about two orders of magnitude over single-rate methods. We concluded that fully asynchronous integrators could be beneficial, but only on problems characterized by a very high separation of scales. In our experiments, two of the three test problems exhibited such a degree of separation, but those problems are fairly simple. A larger-scale parallel test demonstrated the need for careful selection of time-step groups so as to ensure fewer discrete events. A speedup factor of four was demonstrated on this stellar cluster dynamics problem.

References

  1. Gear, C. W., and D. R. Wells, “Multirate linear multistep methods.” BIT 24(4), 484 (1984). http://dx.doi.org/10.1007/BF01934907
  2. Sand, J., and Skelboe, S., “Stability of backward Euler multirate methods and convergence of waveform relaxation.” BIT 32(2), 350 (1992). http://dx.doi.org/10.1007/BF01994887
  3. Engstler, C., and C. Lubich, “Multirate extrapolation methods for differential equations with different time scales.” Computing 58(2),173 (1997). http://dx.doi.org/10.1007/BF02684438
  4. Savenco, V., “Construction of a multirate RODAS method for stiff ODEs.” J. Comput. Appl. Math. 225(2), 323 (2009). http://dx.doi.org/10.1016/j.cam.2008.07.041
  5. Savcenco, V., W. Hundsdorfer, and J. G. Verwer, “A multirate time stepping strategy for stiff ODEs.” BIT 47(1),137 (2007). http://dx.doi.org/10.1007/s10543-006-0095-7
  6. Kofman, E., and S. Junco, “Quantized state systems. A DEVS approach for continuous system simulation.” Trans. Soc. Comput. Simul. Int. 18(3), 123 (2001).
  7. Kofman, E., “A second order approximation for DEVS simulation of continuous systems.” Simul. 78(2), 76 (2002).
  8. Allen, S. M., and J. W. Cahn, “A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening.” Acta Metall. 27(6), 1085 (1979). http://dx.doi.org/10.1016/0001-6160(79)90196-2
  9. Pearson J. E., “Complex patterns in a simple system.” Science 261(5118),189 (1993). http://dx.doi.org/10.1126/science.261.5118.189