Frederic Hartemann (16-FS-043)
Abstract
We have established the feasibility of generating quantum-controlled, ultrahigh-brightness electron beams via barrier-suppression ionization (BSI), linear space-charge expansion, and trapping in a high-gradient radio-frequency (rf) structure. Our demonstration is based on careful, fully three-dimensional (3D) simulations of the space-charge evolution of an electron micro-bunch accelerated by a strong rf field (100 MV/m). For low-charge operation (fC–pC), the beam brightness is typically several orders of magnitude beyond the current state of the art—in the 1016–20 A/m2 range. The details of the quantum photoelectron state after BSI have not yet been fully studied, but initial simulations show no significant performance degradation compared to a cold initial distribution, which is expected because the initial spatial distribution of the phase space dominates the beam dynamics. This new concept for electron beam generation opens the possibility of coherent radiation emission at very short wavelengths (sub-ångstrom) with modest beam energies (10–100 MeV).
Background and Research Objectives
Electron beam quality is a fundamental driver for numerous important applications ranging from coherent and incoherent compact x-ray light sources, to electron diffraction imaging, laser-driven acceleration, and high-energy physics at the luminosity frontier. Generating electron beams with exceptional brightness by controlling their evolution directly from the quantum level via BSI, and using a few optical cycles and an absolutely phase-stabilized laser (all the way to high gradient capture and acceleration linac) would offer the possibility of generating coherent hard x-rays (hundreds of kiloelectronvolts) at low electron energy (one-hundred megaelectronvolts) via laser beat-wave free-electron lasing, within a very compact footprint (tabletop).
Within this context, the goal of this project was to establish the feasibility of generating quantum-controlled, ultrahigh brightness electron beams via BSI,1–3 linear space-charge expansion,4 and trapping in a high-gradient rf structure. Our technical motivation is to develop next-generation photoelectron guns with unprecedented beam quality for coherent x-ray generation in a very compact footprint. This would enable deployment on the National Ignition Facility (NIF) for radiography of dense, compressed matter. The plan was to evaluate the initial BSI electron-beam phase space to propagate the beam in the extraction region, fully accounting for space-charge effects, and to simulate acceleration in a strong rf field and final phase-space density. This was accomplished by using advanced 3D computer codes describing BSI, space charge, and rf dynamics.
Scientific Approach and Accomplishments
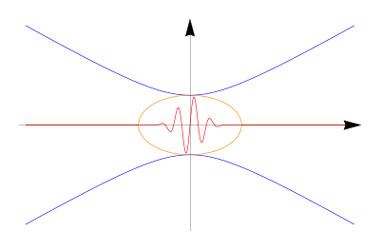
For complete simulations of the electron beam dynamics, the initial BSI electron phase space is the starting point; two distinct, but correlated components contribute, namely the spatial and momentum distribution of photoelectrons. For a broad range of incident laser intensities, the BSI probability is proportional to the local square of the laser electric field. From this fact, one can build the initial electron spatial distribution for different laser focal configurations. The overall focal geometry is shown below in Figure 1.
Figure 1. Overview of laser focal geometry. The elliptical region corresponds to intensities sufficient for BSI; the vertical axis corresponds to the linear polarization, while the horizontal axis is along the laser propagation.
In our study, we have considered Gaussian foci, as well as colliding pulses schemes; we have also used simple spherical models to benchmark our simulations. The momentum component of the phase space requires full quantum simulations, obtained by solving the time-dependent Schrödinger equation (TDSE); such computer studies show that the momentum is strongly correlated with the laser polarization state, which we have systematically assumed to be nominally linear and along the rf field. For very tight foci, wavefront curvature results in polarization curvature in the plane of polarization, which can be taken into account by rotating the local coordinate system used for the TDSE. The canonical momentum in the laser field gives the maximum momentum of the BSI electrons: the product of the electron charge and laser vector potential. To simplify our simulations, we have focused on the spatial aspects of the initial phase; this is justified in view of the dominance of space-charge effects in determining the final beam quality over the details of the BSI momentum distribution. We have also further validated this assumption by comparing 0-momentum simulations to both isotropic and delta-function angular distribution with the amplitude of the canonical momentum in the laser field; these show second-order effects dominated by the first-order space-charge mechanisms.
Technically, the code we used is based on solving the Lorentz force equation for macroparticle trajectories in the combined point-to-point electron and proton space-charge fields, and the space and time-dependent accelerating rf field.
Initially, the system is globally neutral, as the electron the Coulomb field of the protons neutralizes space charge. As the rf field begins extracting electrons from the focal region, lensing effects are observed due to the charge imbalance created in the electron–proton plasma. A third region follows, where the electrons interact via point-to-point Coulomb forces, prior to undergoing nearly linear space-charge expansion. The proton lensing and initial space-charge effects determine most of the beam emittance and brightness.
The laser focus influence, which determines the exact initial spatial distribution of BSI electrons and protons, is a determinant factor in the resulting beam quality. For example, as the focal spot size decreases, the Rayleigh length increases quadratically, yielding highly elongated initial photoelectron bunches. In that case, the much stronger space-charge forces along the narrow bunch dimensions tend to quickly bring the bunch aspect ratio toward a more isotropic system, which then undergoes quasi-linear space-charge expansion.
This is important because linear lenses can compensate for the linear correlations in the phase space, resulting in simple rotations of the phase space; the nonlinear effects cannot be alleviated by such techniques and essentially contribute to core emittance of the beam.
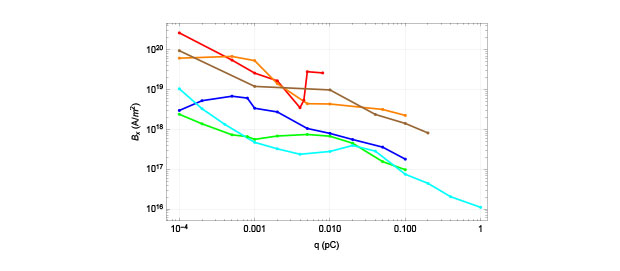
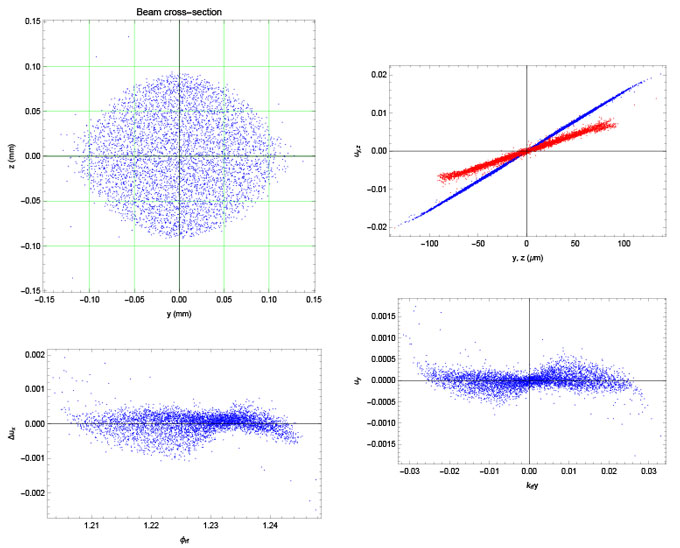
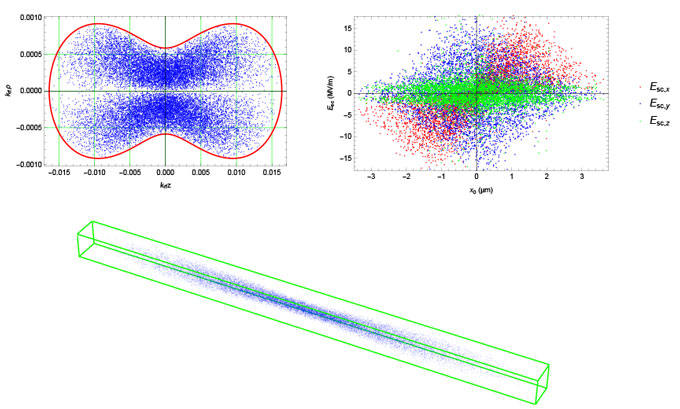
In our simulations, the linear correlations were measured statistically and the appropriate phase space rotation was applied to derive the uncompensable emittance of the resulting electron beam. Brightness is then calculated by accounting for the axial phase as well, using root-mean-square values over the statistical ensemble of macro-particles. For reference, the case of a 2-µm focus for 0.8-µm linearly polarized light interacting with atomic hydrogen (for simplicity), and subjected to 11.424-GHz rf with a peak field of 100 MV/m is documented in Figures 2 and 3. Five-thousand macro-particles are tracked with point-to-point space charge and proton lensing. Figure 4 summarizes a series of simulations where the bunch charge varies, for three different spot sizes: 1, 2, and 3 µm, respectively.
Impact on Mission
The work performed is a key technology enabler toward tabletop coherent x-ray sources. As such it is of direct importance to the Inertial Confinement Fusion and high-energy-density science programs, because it may eventually provide a means to radiograph dense compressed matter at the National Ignition Facility. The laser, nonlinear optics, rf, synchronization, and electron-beam technology aspects of this new electron gun concept are directly relevant to Livermore’s core competency in lasers and optical science and technology. The compact x-ray applications that would directly benefit from this work are an integral component of the core competency in high-energy density science and fit within the mission focus area of inertial fusion science and technology. This project is also highly relevant to the DOE's High-Energy Physics (HEP) program and LANL’s Matter and Radiation in the Extreme (MaRIE) project.
Conclusion
Having identified the key relevant physical processes underlying ultrahigh-brightness, quantum-controlled electron beams generated via BSI, and having established this concept in terms of the production of electron microbunches with unprecedented quality and very low emittance, we strongly suggest that further studies are warranted, including the following salient physics and engineering tasks:
- Develop a fully relativistic point-to-point space charge code, including electromagnetic field retardation effects.
- Solve TDSE with Stark and Zeeman splitting in static magnetic field and rf fields.
- Include static magnetic field for beam focusing.
- Further study laser pulse propagation in low-pressure gas for BSI cell.
- Study electron beam propagation in beam tunnel between BSI cell and accelerator.
- Investigate scattering and emittance growth in a nanometer diamond window.
- Explore electron post-acceleration in rf structure.
- Develop laser integration and focusing schemes.
- Develop beat-wave, free-electron laser parameters for coherent x-ray generation.
The above research and development would provide a roadmap to the engineering design of a prototype BSI gun; simple validation experiments may also complement such follow-on work.
References
- Bauer, D., and P. Mulser, "Exact field ionization rates in the barrier-suppression regime from numerical time-dependent Schrödinger-equation calculations." Phys. Rev. A 59, 569 (1999).
- Brabec, T., and F. Krausz, "Intense few-cycle laser fields: Frontiers of nonlinear optics." Rev. Mod. Phys. 72, 545 (2000).
- Krausz, F., and M. Ivanov, "Attosecond physics." Rev. Mod. Phys. 81, 163 (2009).
- Luiten, O. J., et al., "How to realize uniform three-dimensional ellipsoidal electron bunches." Phys. Rev. Lett. 93, 094802 (2004).