Miguel Morales-Silva (16-ERD-044)
Abstract
To help resolve the experimental controversies of the solid-to-liquid phase transition of metallic hydrogen and move the field towards a definitive understanding of the metallization and dissociation processes in dense hydrogen, we explored the use of advanced first-principles methods based on density functional theory to calculate the vibrational and optical properties of hydrogen at high pressure. Density functional theory is a computational quantum-mechanical modeling method to investigate the electronic structure of many-body systems. With this project, we were able to use first-principles simulations based on density functional theory to calculate the vibrational and optical properties of hydrogen at high pressure. An accurate understanding of these properties is essential to the understanding of metallization and dissociation in hydrogen at extreme conditions. The first experimental observations of metallization for liquid hydrogen produced conflicting results about the character and location of the transition. The calculations we performed for this project will help resolve hydrogen's phase-transition controversies, which is of importance to stockpile stewardship science as well as astrophysical research. We previously showed that density functional theory is unlikely to have enough accuracy by itself to correctly resolve questions about hydrogen's phase diagram. Our research represents the first implementation of this advanced first-principles-based method to the study of high-pressure hydrogen.
Background and Research Objectives
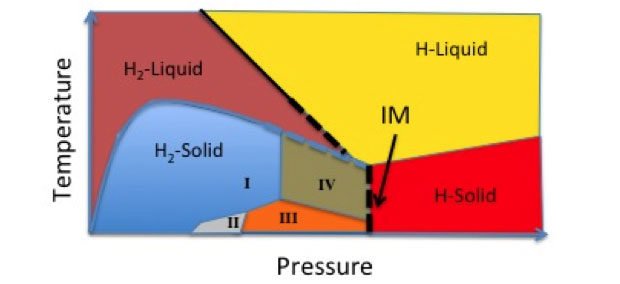
Hydrogen has a unique place in the field of planetary science and high-pressure physics.1 It is the most abundant element in the universe, comprising many astronomical objects such as Jupiter and Saturn in our own solar system and a large number of other objects discovered in the past decade. An accurate understanding of its phase diagram at high pressures and temperatures (Figure 1) is critical for the proper understating of Jovian planets’ interior structure, evolution, and formation. In addition, the experimental observation of metallic hydrogen has become one of the greatest challenges in the high-pressure community. Over the last years, several groups have reported the observation of metallic hydrogen in both solid and liquid phases.2,3 Unfortunately, all predictions are highly controversial, and in the case of the liquid, both reported experiments strongly disagree on the location of the transition (by over 200 GPa). Advanced first-principles methods are needed to help resolve the experimental controversies and move the field towards a definite understanding of the metallization and dissociation processes in dense hydrogen.
For the last two decades, theoretical efforts have centered on the use of density functional theory, mostly within the Purdue–Burke–Ernzerhof approximation for the exchange-correlation energy, to study the relative stability and phase boundaries in the solid. Density functional theory is a computational quantum-mechanical modeling method used in physics, chemistry, and materials science to investigate the electronic structure of many-body systems—in particular, atoms, molecules, and their condensed phases. As we have recently shown, it is unlikely that density functional theory, particularly with the Purdue–Burke–Ernzerhof approximation, has sufficient accuracy to correctly resolve the current questions about the phase diagram of hydrogen, particularly if using energetics to identify equilibrium phases. In addition, nuclear quantum effects have shown to be critical in the proper description of hydrogen at these conditions, so any calculation that hopes to be predictive needs to account for these effects directly and accurately. Fortunately, accurate quantum Monte Carlo calculations have been used to benchmark a large number of typical approximations to the exchange-correlation energy in density functional theory.4 This work lead to the identification of the best-suited functionals to use in the study of high-pressure hydrogen, both from the point of view of accurate relative energies and accurate structural and vibrational properties.
Building on the successful identification of accurate density functional theory functionals for high-pressure hydrogen, we extended the study of hydrogen at extreme conditions by calculating the optical and vibrational properties of the liquid near the metallization and dissociation transition using a combination of quantum Monte Carlo and optimal density functional theory methods.
Scientific Approach and Accomplishments
The calculations for this project were based on a combination of quantum Monte Carlo methods and density functional theory, using optimal exchange-correlation functionals for hydrogen. We performed coupled electron–ion Monte Carlo calculations and ab initio path-integral molecular dynamics calculations to study the equilibrium properties of liquid hydrogen at pressures and temperatures near the metallization and dissociation regime in the liquid. The resulting trajectories were analyzed to calculate optical and vibrational properties. We used a combination of hybrid density functional theory calculations and perturbative calculations based on the GW approximation method to obtain optical properties—Green's function G and screened interaction W is a method that reduces the gap between experimental observations and theoretical predictions of the properties of atoms and molecules used to calculate the self-energy of a many-body system of electrons.
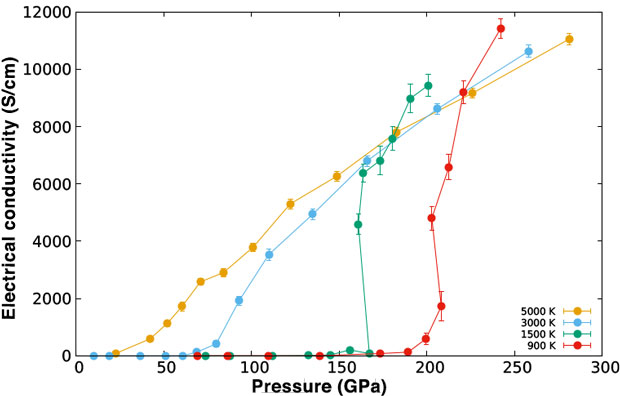
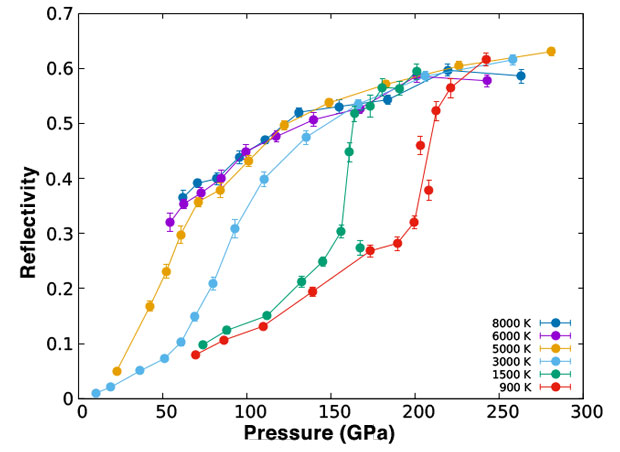
We studied the reflectivity, electrical conductivity, absorption coefficient, and thermal conductivity in the desired temperature and density regime. The results were compared against previous experimental calculations and against the limited experimental measurements available. Figures 2 and 3 show the reflectivity and electrical conductivity of the hydrogen liquid as a function of pressure for various temperatures. The liquid–liquid transition on hydrogen is clearly observed as a discontinuous change on both properties as a function of pressure. In the case of the electrical conductivity, the change is large and abrupt. In the case of the reflectivity, on the other hand, the liquid displays a significant reflectivity of about 20 to 30% even on the insulating regime. As a consequence, the signature of the liquid–liquid transition on the reflectivity is much smaller and subtler. Experimental identification of the first-order transition then requires a carefully measured pressure dependence of the reflectivity to produce the correct interpretation, when only measurements of the reflectivity are made. This helps explain some of the recent controversies on the observed character of the transition between various experimental platforms.
Impact on Mission
Understanding and correctly modeling hydrogen at high pressure is critical to advancing several Livermore missions and core competencies, including stockpile stewardship, high-pressure physics, and developing new materials through advanced manufacturing. Developing and applying novel methods to the study of materials at extreme conditions, through the calculation of structural, optical, and vibrational properties of dense materials strengthens Livermore’s core competency in high-energy-density science and technology.
Conclusion
This project enabled the study of the optical and vibrational properties of hydrogen at extreme conditions using advanced first-principles methods. The results of this work will help resolve an important controversy in the field of high-pressure physics regarding the nature of the metallization and dissociation transition on liquid hydrogen, as well as conflicting experimental observations of the location and character of the transition. Our research results will be an important step leading to identification of the structure of hydrogen's solid phases, because infrared and Raman spectral data sets are the only experimental signatures measured in high-pressure experiments with hydrogen, and any successful identification of equilibrium phases and phase transitions from a theoretical calculation needs to successfully reproduce the vibrational signatures of the transition across the phase diagram.
References
- McMahon, M., et al., “The properties of hydrogen and helium under extreme conditions.” Rev. Mod. Phys. 84, 1607 (2012).
- Knudson, D., et. al., “Direct observation of an abrupt insulator-to-metal transition in dense liquid deuterium.” Science 26, 1455 (2015).
- Dzyabura, M., I. Zaghoo, and F. Silvera, “Evidence of a liquid-liquid phase transition in hot dense hydrogen.” Proc. Nat. Acad. Sci. 110, 8040 (2014).
- Clay, C., et al., “Benchmark of exchange-correlation functionals for high-pressure hydrogen using quantum Monte Carlo.” Phys. Rev. B 89, 184106 (2014).