Variable Precision Computing

Jeffrey Hittinger (17-SI-004)

Executive Summary

Disruptive changes in high-performance computing hardware, where data motion is the dominant cost, present us with an opportunity to reshape how numbers are stored and moved in computing. Our project is developing methods, tools, and expertise to facilitate the use of mixed and dynamically adaptive precision numbers, allowing us to store and move the minimum number of bits required to perform a given calculation and help ease the data motion bottleneck on modern computer architectures.

Project Description

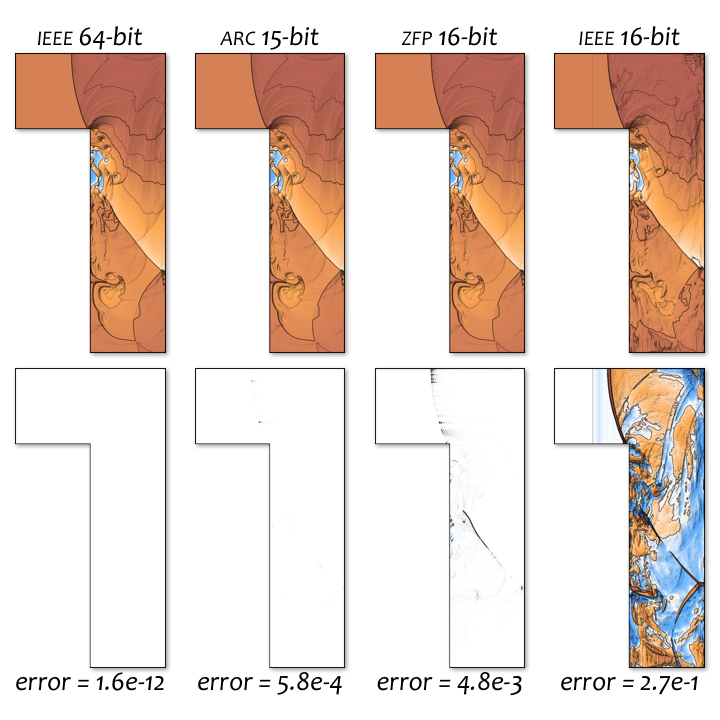
Decades ago, when memory was a scarce resource, computational scientists routinely worked in single precision (a computer number format) and were adept in dealing with finite-precision arithmetic. Today, we compute and store results in 64-bit double precision even when very few significant digits are required. Often, more precision is used as a simple guard against corruption from roundoff error instead of making the effort to ensure algorithms are robust to roundoff. In other cases, only isolated calculations require additional precision (e.g., tangential intersections in computational geometry). Many of the 64 bits represent errors (truncation, iteration, or roundoff) instead of useful information. This over-allocation of resources wastes power, bandwidth, storage, and floating-point operations. We are developing novel methods, tools, and expertise to facilitate the effective use of mixed and dynamically adaptive precision in Lawrence Livermore applications. We are also producing software tools aiding development of portable mixed and adaptive precision codes, to ensure our techniques are adopted by code developers. Calculations benefit from easy maintenance of mixed-precision code and incorporation of mixed-rate compression into data analysis and input and output. Increasing precision adaptively can accelerate search and ensemble calculations in uncertainty quantification and mathematical optimization. Variable precision also allows greater accuracy at lower cost in data analysis tasks such as graph ranking, clustering, and machine learning applications.

If successful, this project can result in significant computational savings while increasing scientific throughput by up to an order of magnitude. Variable precision computing will enable 4 to 100 times less data storage and 2 to 10 times greater computational throughput for many applications. Our software tools and libraries will enable widespread development of portable mixed and adaptive precision codes. Demonstration of the benefits of compression and variable-length data types will justify hardware support in future procurement. We are pursuing three integrated and concurrent thrusts: (1) develop algorithms and software to support the use of adaptive precision through a floating-point compression algorithm and a hierarchical multi-resolution data format for problems for which errors do not accumulate such as input and output; (2) address the use of variable precision within numerical algorithms using standard data representations; and (3) consider new formats for representing floating-point numbers and their utility in numerical algorithms. For all these objectives, we are demonstrating the relevance of new variable precision algorithms in Laboratory applications and demonstrating a subset of techniques on a new advanced RISC machine (commonly known as an ARM) and graphics processing unit cluster.

Mission Relevance

Our project supports the NNSA goal of shaping the infrastructure to assure we have the core capabilities necessary to execute our mission responsibilities. Facilitating the use of mixed and dynamically adaptive precision computing applications will directly advance Livermore's high-performance computing, simulation, and data science core competency.

FY17 Accomplishments and Results

In FY17 we (1) developed a data structure for adaptive rate compression based on zero false-positive compressed blocks; (2) investigated new variable-precision representations and evaluated their accuracy; (3) implemented a prototype of error transport for multi-level data representation, applying it to a parabolic model problem; (4) studied effects of single precision on k-dimensional eigenvector embeddings for machine learning and implemented an iterative, mixed-precision eigensolver; (5) developed a new C++ wrapper library for floating-point analysis; and (6) implemented a prototype tool for transforming access functions of fixed number type in the original code to the access functions of a variable-precision number type.

Figure 1. Results of inline data compression for a compressible gas dynamics simulation of a shock wave propagating through an L-shaped domain. The initial condition is a two-state solution with a planar shock in the short leg of the L separating the two states. The top images plot the mass density at the final time, and the bottom images plot the deviation of the solution (roundoff error) from the IEEE 64-bit solution (double precision); the deviation for double precision is relative to IEEE 128-bit solution (quad precision). Results using the new Adaptive Rate Compression (ARC) generalization of ZFP with effectively 15 bits per value and the zero false-positive (ZFP) lossy compression algorithm fixed at 16 bits per value are plotted; thus the data compression rate is roughly a factor of four. The solution state is stored compressed and then decompressed by 4-by-4 blocks on demand at each time step, advanced in time, and then recompressed by block. From the plots, it is clear that the compression scheme incurs considerably less error than the closest equivalent IEEE type, IEEE 16-bit (or half precision), with ARC possessing even less error than ZFP. Quantitatively, the RMS error in ZFP is two orders of magnitude less than that in half precision for the same storage cost, and ARC is almost an order of magnitude lower than ZFP. For a similar level of error to that in ZFP, ARC could provide a compression rate higher than a factor of four, which would significantly improve bandwidth limitations on data transfers.

Publications and Presentations

Hittinger, J. A. 2017. "Making Every Bit Count: Variable Precision?" Big Data Meets Computation. January 30-February 3, 2017, Los Angeles. LLNL-ABS-718238.

Lindstrom, P. G. 2017. "Error Distributions of Lossy Floating-Point Compressors." 2017 Joint Statistical Meetings. July 29-August 3, 2017, Baltimore. LLNL-CONF-740547.

Schordan, M., J. Huckelheim, P. Lin, H. M. Gopalakrishnan, 2017. "Verifying the Floating-Point Computation Equivalence of Manually and Automatically Differentiated Code." Correctness 2017: First International Workshop on Software Correctness for HPC Applications. November 12, 2017, Denver. LLNL-CONF-737605.