1. Home
  2. Report Archives
  3. FY2015 LDRD Annual Report
  4. Nuclear, Chemical, and Isotopic Science and Technology
  5. Complex Electronic Structure of Rare Earth Activators in Scintillators

Complex Electronic Structure of Rare Earth Activators in Scintillators

Per Daniel Aberg (13-ERD-038)

Abstract

Interest in scintillator materials that fluoresce because of interaction with a charged particle or photon has surged recently thanks to large-scale applications in nuclear and radiological surveillance, high-energy physics, and medical imaging. One of the current goals is to develop materials with improved energy resolution to detect fissile materials at ports, borders, and airports with a low probability of error. For this project, we focused on the study of the electronic energy levels of rare earth activators in these materials using theoretical modeling and experimental validation to provide information on key microscopic events such as the hole and electron-capture cross section by activators, for which there is currently no reliable method. Our plan is to implement a novel algorithm for computation of the rare earth electronic structure, in relation to crystal host bands, via atomic physics and dynamical mean field theory, and validate the results using x-ray absorption spectroscopy and x-ray emission spectroscopy measurements. To aid and further understanding of the microscopic mechanisms behind the scintillator non-proportionality that leads to degradation of the attainable energy resolution, we developed theoretical and experimental algorithms and procedures to determine the position of the 4f energy levels of rare earth dopants relative to the host band-edge states.

Background and Research Objectives

Understanding the scintillation mechanism of rare earth doped scintillators requires a detailed understanding of the electronic structure of the dopant–host complex. In particular, to ensure that excitons or separate electron or hole carriers can be trapped on the rare earth material and thus ultimately produce photon emission, its 4f and 5d electron levels need to reside within the forbidden band gap region. Furthermore, this electronic structure also serves as a starting point to compute, for example, carrier capture/emission rates. Standard density functional theory is unfortunately not capable of treating the rare earth material open-shell structure and results in partially unoccupied rare earth 4f levels that always reside inside the gap. More elaborate cluster calculations using modern quantum mechanical approaches lack proper band alignment between the periodic host and model cluster. Viewed in this light, this project succeeded both in developing computational tools to address this issue, and in designing and performing experiments using x-ray techniques to validate the modeling.

Scientific Approach and Accomplishments

We modeled the 4f states using two different approaches, outlined below. The first approach followed an idea of Miyake and Aryasetiawan for the localized states in correlated 3d transition metals.1 This approach consisted of constructing an effective 4f Hamiltonian by extracting screened Coulomb matrix elements in the constrained random-phase approximation for a rare earth doped into a large super-cell. To that end, we began implementation into the popular software package VASP2 based on the projector augmented-wave method, which is a technique used in ab initio electronic structure calculations that allows density functional theory calculations to be performed with greater computational efficiency.3 The projector augmented-wave method has proven very successful both in terms of efficiency and accuracy for density functional theory calculations of point defects and dopants in large super-cells, but its accuracy for this application was at the time unknown. While we were able to exactly reproduce Hartree–Fock results for the unscreened matrix elements, we found that the current state-of-the-art projector augmented-wave representation of the dielectric response function needed to calculate the random-phase approximation matrix elements lacks the needed accuracy. In fact, the matrix elements turned out to be severely underestimated. This was later verified in another context by the VASP group.4

To address this shortcoming, we chose to represent the response function using the so-called mixed basis set instead.5 This type of basis set is specifically designed to accurately handle products of wave functions within the linear muffin-tin orbital (the linear muffin-tin shape approximates the potential field in an atomistic environment) or the projector augmented-wave formalisms. Thus, this basis set is suitable for both calculations of the response functions as well as of the screened Coulomb matrix elements. We chose to modify the existing, very-well-documented GW code (GW is an approximation of the self-energy of a many-body system of electrons) of Jiang et al., called FHI-gap,6 with input density-functional-theory wave function and energies from the WIEN2k code.7

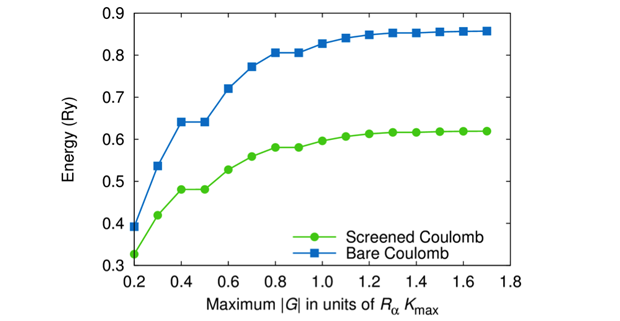
The FHI-gap is, like most GW codes, specifically optimized to efficiently compute energy corrections for smaller unit cells. In particular, the parallelization is not optimal in terms of memory, because every node needs to store the full response function and Coulomb matrices. This situation quickly leads to exceeding the available memory and cannot be alleviated by increasing the number of nodes. We therefore re-parallelized the entire code using scaLAPACK, which is a subset of the popular netlib LAPACK routines that are redesigned for distributed memory parallel computers.8 As a result, we are now able to calculate screened matrix elements for large cells—see Figure 1 for an example of the rare earth element praseodymium in a 12-Å cell. However, going beyond this will prove significantly harder in terms of memory requirements. Therefore, we developed another alternative.

Figure 1. convergence of screened and unscreened coulomb matrix elements for the trivalent praseodymium ion praseodymium(iii) in a 12-å cell.
Figure 1. Convergence of screened and unscreened Coulomb matrix elements for the trivalent praseodymium ion praseodymium(III) in a 12-Å cell.

 

A second, simpler but more effective, approach was born out of the development of a new co-doping scheme for cerium-doped lanthanum(III)–bromide leading to improved detector performance at Delft University in Holland.9 At the time, the mechanism behind the improvement was unknown, but we were able to solve this problem.10 However, if this model is to be correct, it should also explain the observed Stokes shifts in the absorption/emission spectra of cerium. (A Stokes shift is the difference between positions of the band maxima of the absorption and emission spectra of the same electronic transition.) We did find three different cerium–strontium–(bromine-vacancy) triple-complexes, but the challenge was to calculate their absorption/emission lines. To accomplish that, we first defined a subspace of the density functional theory Kohn–Sham states corresponding to the cerium-4f states by selecting only states whose projection onto spherical harmonics with l = 3 exceeds a suitably chosen threshold. This is made possible by the localized nature of the rare earth 4f states (and only works if the 4f states are not hybridized with the host bands). In this particular way, a Ce 4f15d0 → 4f05d1 excitation can be emulated by introducing a second Fermi level for the 4f subspace. Therefore, the resulting total energies are variational, and this allows for excited-state structural relaxations. Using this scheme, we were able to calculate the Stokes shift that agreed very favorably with experiment.11

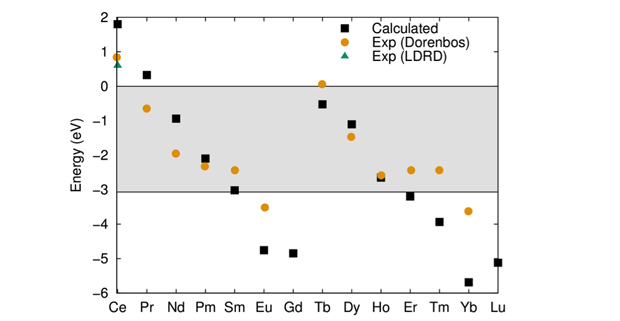
The same approach—without modification—could not be applied to the rest of the rare earth series in the same material because of the un-physical hybridization of the 4f levels with the host ligands. This makes the identification of the 4f subspace ill defined. To overcome this issue, we applied a local constant potential to the 4f states within the projector augmented-wave sphere that shifts the associated states energetically away from the host bands. Then, the un-physical hybridization is removed and we can perform the subdivision of the orbital spaces and apply an equal occupation to all 4f bands. Once converged, the 4f levels are shifted back by the negative of the applied potential, and the level positions with respect to the host band edges can be determined. In this way, we studied all the rare earths doped into lanthanum(III)–bromide and compared the results to the values we obtained in this project with those in existing literature. The results, shown in Figure 2, are very agreeable and show that the developed methodology can predict the relative positions of the 4f levels, thus successfully completing one of the major goals of this project.

Figure 2. experimental and calculated position of the 4f levels for all rare earths in lanthanum(iii)–bromide. experimental data is from this project and existing literature.<sup>12</sup>
Figure 2. Experimental and calculated position of the 4f levels for all rare earths in lanthanum(III)–bromide. Experimental data is from this project and existing literature.12

 

For the experimental portion of our project, we applied x-ray absorption spectroscopy, x-ray emission spectroscopy, and resonant photoemission spectroscopy to determine the cesium 4f state of the activator with respect to the top of the valence band. For the cerium-activated yttrium–aluminum–perovskite scintillator, we determined that the cerium 4f position relative to the top of the valence band to be 1.8 ± 0.5 eV. In case of a cerium-activated lanthanum(III)–bromide scintillator, it is determined to be 0.6 ± 0.4 eV. The lanthanum(III)–bromide value differs by roughly 1 eV compared to the theoretical prediction, but that is to be expected given the choice of exchange correlation functional. Application of a hybrid functional together with the theoretical approach developed here will further improve upon this value and will be the subject of further research.

Impact on Mission

The goal of this project was to develop unique computational and experimental capabilities to address limiting factors in scintillator radiation detector functionality. As such, it is well aligned with the Laboratory’s mission in nonproliferation. Furthermore, it supports the DOE’s newly established Energy Innovation Hub and the search for rare earth element substitutes. We expect that the framework developed here will enable incorporation of strong electron correlation effects in the equation-of-state models for actinides, which is highly relevant to stockpile stewardship science and LLNL’s core competencies in nuclear, chemical, and isotopic science and technology and high-performance computing, simulation, and data science.

Conclusion

We successfully developed theoretical and experimental methodologies to study the position of rare earth 4f levels in relation to the host band edges. Our next steps will be to continue our investigation on thermal non-radiative quenching in cerium-doped yttrium–aluminum–perovskite and other materials, as well as developing a methodology for carrier capture cross sections within the context of a newly funded NNSA project in nonproliferation research and development. We will also seek applications for phosphor research within the context of the Critical Materials Institute led by Ames Laboratory at Iowa State University.

References

  1. Miyake, T., and F. Aryasetiawan, “Screened Coulomb interaction in the maximally localized Wannier basis.” Phys. Rev. B 77, 085122 (2008).
  2. Kresse, G., and J. Hafner, ”Ab initio molecular dynamics for liquid metals.” Phys. Rev. B 47, 558 (1993).
  3. Blöchl, P. E., “Projector augmented-wave method.” Phys. Rev. B 50, 17953 (1994).
  4. Klimeš, J., M. Kaltak, and G. Kresse, “Predictive GW calculations using plane waves and pseudopotentials.” Phys. Rev. B 90, 075125 (2014).
  5. Aryasetiawan, F., and O. Gunnarsson, “Linear-muffin-tin-orbital method with multiple orbitals per L channel”, Phys. Rev. B 49, 7219 (1994).
  6. Jiang, H., et al., “FHI-gap: A GW code based on the all-electron augmented plane wave method." Comp. Phys. Commun. 184, 348 (2013).
  7. Blaha, P., et al., “WIEN2k, An augmented pane wave + local orbitals program for calculating crystal properties.” Vienna University of Technology, Vienna, Austria (2001).
  8. Blackford, L. S., et al., ScaLAPACK users’ guide. Society for Industrial and Applied Mathematics, Philadelphia, PA (1997).
  9. Alehkin, M. S., et al., “Improvement of γ-ray energy resolution of LaBr3:Ce3+ scintillation detectors by Sr2+ and Ca2+ co-doping.” Appl. Phys. Lett. 102, 161915 (2014).
  10. Åberg, D., et al., “Origin of resolution enhancement by co-doping of scintillators: Insight from electronic structure calculations.” Appl. Phys. Lett. 104, 211908 (2014).
  11. Erhart, P., et al., “First-principles study of codoping in lanthanum bromide.” Phys. Rev. B 91, 165206 (2015). LLNL-JRNL-663482. http://dx.doi.org/10.1103/PhysRevB.91.165206
  12. Dorenbos, P., et al., “Level location and spectroscopy of Ce3+, Pr3+, Er3+, and Eu2+ in LaBr3”, J. Lumin. 117, 147 (2006).

Publications and Presentations

  • Erhart, P. et al., “First-principles study of codoping in lanthanum bromide.” Phys. Rev. B 91, 165206 (2015). LLNL-JRNL-663482. http://dx.doi.org/10.1103/PhysRevB.91.165206
  • Yu, S.-W., et al., "Atomic origin of 3d94f1 configuration in La3+ solids." J. Phys. Condens. Matter 27(40), 405501 (2015). LLNL-JRNL-668475. http://dx.doi.org/10.1088/0953-8984/27/40/405501
  • Yu, S.-W., Ce 4f1energy level in the band gap of LaBr3(Ce) scintillator by resonant photoelectron spectroscopy. (2015). LLNL-JRNL-675674.
  • Yu, S.-W., et al., "Energy levels of the Ce activator relative to the YAP(Ce) scintillator host." J. Phys. Condens. Matter 27(18), 185501 (2015). LLNL-JRNL-652413. http://dx.doi.org/10.1088/0953-8984/27/18/185501