Duane Liedahl (17-FS-018)
Abstract
The extraction of physical quantities from experimental x-ray spectra often involves atomic-physics-based computer codes that are used to generate model (theoretical) spectra, which are then compared to the data. Among the quantities of interest is the electron temperature. If the measured x-ray spectrum arises from an isothermal plasma, these codes are effective, at least for those cases where relatively simple ions are used as diagnostics. One can usually find a temperature, (that is, a model spectrum generated at that temperature), that reproduces the data reasonably well. However, if the plasma is not isothermal, it is, as a rule, impossible to find a single-temperature model that fits all the data. Moreover, if one assumes at the outset that the plasma is isothermal, it is easy to fall into the trap of using an exclusive subset of a spectrum to make claims about the temperature, claims that may be somewhat in error or grossly in error, depending on the actual temperature distribution. We explored the feasibility of developing a computational framework that can be used to perform an inverse process for determining the temperature distribution from a measured spectrum, rather than generating spectra for a given temperature distribution. We approached the problem by assuming that any a priori concept of “the temperature” is ill-founded. Instead, we allowed for arbitrary temperature distributions, then used the computational framework to extract these distributions.
Background and Research Objectives
Our work applies to high-temperature (a few kiloelectronvolts) laser-produced plasmas in non-local-thermodynamic-equilibrium (NLTE). Throughout, we intend the term “temperature” to refer only to the free electron population, not to the ions nor the radiation field. In fact, the effects of radiation fields and any possible ion–electron disequilibrium can be almost entirely neglected for the problem at hand.
In laser-produced plasmas, electrons are heated directly by a laser. A given free electron, in the simplest scheme, exchanges kinetic energy with other free electrons, as well as ions, and radiates part of its energy through bremsstrahlung emission. Through these interactions, the electron population tends toward a Maxwellian energy distribution characterized by a temperature. Ions adjust to this temperature, establishing a balance among the various charge states and a distribution among the energy levels within each charge state. An accounting of the atomic processes determining the charge state distribution and level populations shows that radiative recombination, dielectronic recombination, three-body recombination, collisional ionization, and collisional excitation all depend on temperature. Since the local line emissivity spectrum is determined by the excited level population distribution and the radiative decay rates, the local spectrum is largely a consequence of the local temperature.
The connection between the spectrum and the temperature, as regards x-rays, began to be fully exploited in the 1970s, when computer codes that process atomic data were applied to solar physics research and studies of tokamak physics. The appearance of such codes was concomitant with community-wide awareness of the need to upgrade the accuracy and size of the theoretical atomic databases. There are also experimentally-derived databases, but these are predominantly maintained and used for the purposes of line identification and establishing precise line energies. Yet after four decades of progress, we are far from convergence. Not only do various calculations by independent researchers disagree with each other, but more importantly, it is clear that calculations often fall short of accounting for experimental data.
One example worth noting is the x-ray spectrum of gold in the few-kiloelectronvolt temperature range. Given its use in experiments related to Inertial Confinement Fusion (ICF), gold is an especially high-profile example of a complex atom that is notoriously difficult to model. To address this difficulty, one could envision a set of experiments wherein gold spectroscopic data are acquired over a range of temperatures and densities, which are then used to benchmark theoretical modeling efforts. Possibly, these results could be incorporated directly into plasma hydrodynamics codes used for simulating hohlraum physics. This leaves the question as to how we can measure the temperature of a gold plasma if we do not trust the gold calculations to give us that from the spectrum. (Of course, if we did trust the calculations, we would have no need of an experiment of this kind.) The answer is to use tracer elements , which are lower Z elements ionized into the K shell (ground-level-bound electrons only in n = 1). A general rule is: fewer bound electrons mean more accurate calculations. In other words, when the nuclear charge dominates the atomic potential, current theoretical techniques are more reliable. Doping the gold plasma with an element in the fourth row of the periodic table (vanadium, for example) provides the opportunity to measure gold spectra from plasmas of known temperature, if we can determine the temperature from the tracer spectrum.
It is this last “if” that provided the motivation for our study: if we can determine the temperature from the tracer spectrum. The problem lies not with the atomic physics calculations or the ability of experimentalists to obtain high-quality K-shell spectra, but with the two words “the temperature.” There is no guarantee that a laser-produced plasma has one and only one temperature at any given time. It is more likely that the plasma volume exists over a range of temperatures. This is certainly true inside a hohlraum, for example. There may be ample reason to suspect that the same is true of laser-irradiated foils. Qualitatively speaking, we know that these plasmas get hotter over the duration of a few-nanoseconds laser pulse, and it might take a leap of faith to assume that the entire volume heats up uniformly. We also know that the laser burn-through proceeds from the outside in. Therefore, we expect a spatial variation of the temperature at a fixed time. The idea of “the temperature” is meaningless if we adhere to this general picture.
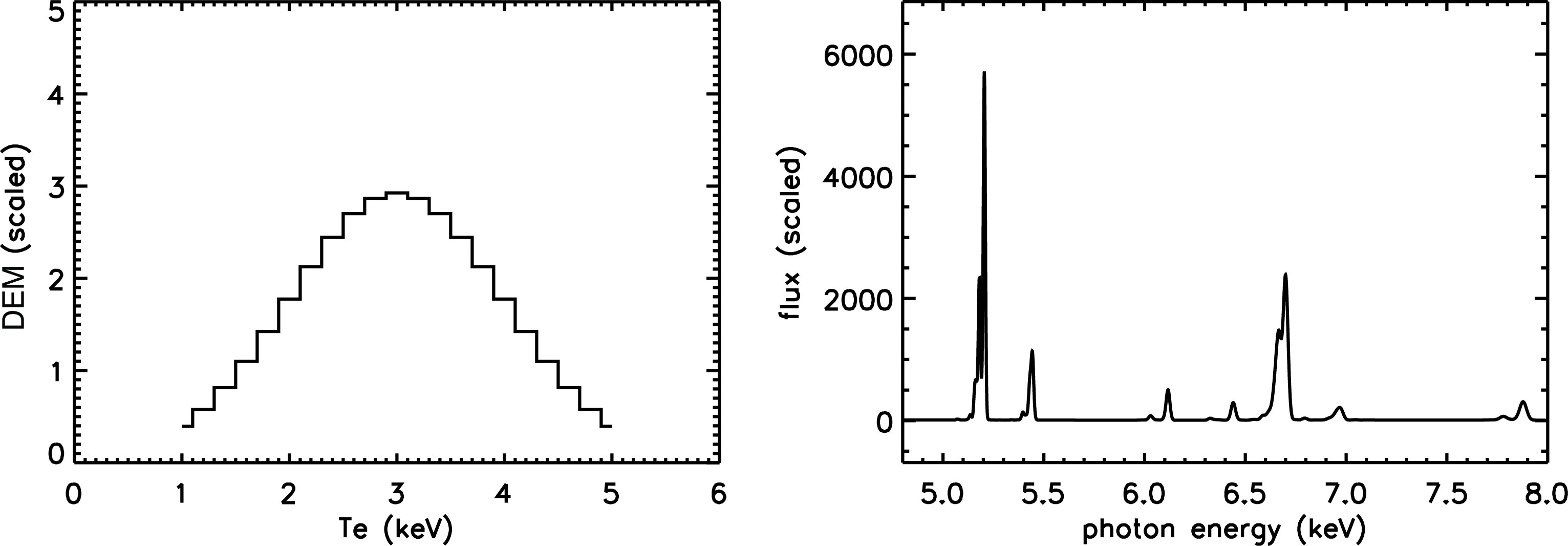
The high-temperature NLTE plasmas under consideration produce x-ray line emissions as a result of two-body (electron–ion) interactions. Therefore, the local radiative power of a small volume element is proportional to a density-squared times the volume of this particular zone times a function of temperature that accounts for the overlap of all the various cross-sections with the local Maxwellian. Suppose that adjacent to this first volume element is another, but with a different temperature. This second volume element has its own density-squared times a volume. This quantity is called an emission measure, and an emission measure can be assigned to each temperature interval. For example, consider a temperature interval, say 2.1–2.2 keV. Step through the cell-delineated volume, and wherever the temperature falls into this range, add the density-squared times volume to the running total for the 2.1–2.2 keV interval. Proceed in this way for the next temperature interval, until the entire plasma volume is accounted for. We can then define a new quantity—the emission measure per temperature interval—called the differential emission measure (DEM). The dimensions of the DEM are inverse volume times inverse temperature. The total power at a given photon energy becomes a temperature integral of the product of the DEM and the radiative power at that photon energy and temperature.
We always discretize the temperature scale, although it is formally an integral. The radiative power at each photon energy (also discretized) and temperature can thus be written as a two-dimensional matrix, which we label L. The DEM is a set of weights, one for each temperature interval. (Typically, we might have a temperature grid that runs from 1–5 keV, subdivided into 0.2 keV intervals; see Figure 1). We can write the DEM as a vector, labeled D, and cast the process of generating a multi-thermal spectrum as a straightforward matrix multiplication: LD = P, where P is a one-dimensional radiative power vector, specified at each photon energy. This formalism, when broken down, is consistent with the intuitive notion that we can add up spectra at different temperatures, with some method of weighting, to produce a composite spectrum. Here the weighting is the DEM, which is the proper weighting for plasmas that radiate via two-body interactions.
While, as described above, it is straightforward to generate a synthetic spectrum based upon a multi-temperature distribution, reversing the process—inferring the temperature distribution D from a known spectrum P—is an example of an inverse problem and is not at all straightforward. Our project goal was to devise a robust program of spectral fitting that would allow us to extract the temperature structure through an inversion process.
Scientific Approach and Accomplishments
Construction of the L matrix proceeds through the use of the SCRAM (Hansen et al. 2007) atomic kinetics code to generate isothermal spectra on a photon energy grid spanning the spectral range of interest. One model spectrum constitutes a column of L, and the remaining columns are computed across a temperature grid spanning the likely range of temperatures produced in a given experiment. A typical L matrix has dimensions 7000 × 30 (7000 energy grid points, 30 temperatures), although any particular application may require a larger matrix or allow one that is smaller.
Singular Value Decomposition of the L Matrix
We originally proposed to investigate the feasibility of using the singular-value decomposition or SVD (Strang 1976) to effect an inversion of L, thus yielding D as the product of P and the inverse of the decomposed L. Typical matrix inversion techniques are rightly deserving of suspicion when noise is present; in this case, the P vector is noisy when it represents a spectroscopic measurement, where counting statistics or calibration uncertainties must be accommodated. Mathematical manipulations characterized by this aspect of matrix inversion fall into the category of ill-posed problems.
We started by taking advantage of readily available algorithms provided in the Interactive Data Language (IDL) suite of codes. Given an assortment of noiseless test problems, the SVD performed reliably. However, when different sets of random Gaussian noise were added to an otherwise fixed P vector, solutions varied wildly. This instability is a feature of ill-posed problems.
The SVD decomposes a matrix into three matrices, two of which are orthonormal. The third is a diagonal matrix made up of the singular values. This is the advantage provided by the SVD; one can actually see where the matrix multiplication is causing problems. The inversion issue can be characterized simply by noting that a small number becomes a large number when inverted. By eliminating or damping these unimportant (small) singular values, one hopes that the solution stabilizes. This approach is called regularization.
We implemented a process known as Tikhonov regularization, with the expectation that we would find stable, physically correct solutions. Unfortunately, the regularized SVD approach would routinely return a mix of positive and negative D vector components, with little improvement over the previous simpler approach. Note that a negative component implies that, over some temperature interval, the product of density-squared and volume is negative, which is clearly unacceptable. Regardless of how we tuned the aggressiveness of the regularization, negative components would arise. We are not aware of any procedure that would prevent this.
The decomposition of the L matrix allowed further investigation. Evaluation of the so-called Picard plot, led us to the conclusion that the problem is too ill-posed (Hansen 2010). This seems to be unavoidable, given the nature of the L matrix. In fact, it is more correct to say that the L matrix is too ill-conditioned. For this reason, we thereafter abandoned the SVD approach, and we regard it as infeasible for this application.
The Genetic Algorithm
We proceeded to investigate a genetic algorithm (GA) approach to the problem. A GA code mimics biological evolution in the following ways: (1) it acts on a population; (2) a criterion of fitness exists; (3) the fittest members of the population are more likely to survive than less-fit members; (4) random mutation may occur; and (5) the population evolves, becoming more fit with each generation.
By the usual terminology, each member is referred to as a chromosome, and each chromosome is made up of a gene sequence. For our application, a chromosome corresponds to one realization of the D vector, a set of weights spanning the temperature grid, where each component of D constitutes a gene. We assign a crossover (breeding) probability, a mutation probability, and a mutation amplitude probability distribution.
We work with a population of typically 100 members. Each member is composed of typically 30 temperature weights. In succession, each member generates a trial spectrum (LD=P), based upon the current gene sequence of that particular member. The set of trial spectra are compared to the data spectrum according to the chi-squared statistic. The member with the lowest chi-squared is given the status of “most fit.” This top-performing member then engages, one at a time, with the remainder of the population in the following way: If crossover occurs (according to the probability “roll”), a gene position is chosen randomly, and the gene of the top member replaces the gene of the lower member in that position. Once all members complete this process, each is subjected to mutation. If mutation occurs, a random position is chosen, and the current value in that position is varied randomly. The new set of family members, some modified, some not, becomes the second generation.
Note that by this scheme the top family member is not subject to modification, but passes intact to the next generation. Different versions of the crossover process are in use elsewhere. Our method is a particularly aggressive variant of what is called elitism, where the top member is guaranteed to be replicated and passed on to the subsequent generation. It is not the case, however, that the top member of a given generation survives in perpetuity. Crossover and mutation together always provide a challenge to the longevity of the top member. This is necessary in order to progress toward higher and higher levels of fitness. In any case, the process is repeated, and one finds that the family-average fitness improves generation by generation, with the spectrum being more faithfully reproduced as the DEM distribution evolves.
The evolutionary process is terminated after the rate of improvement levels off, or after a set number of generations (a few thousand usually suffices). Negative solutions do not arise: a great advantage. It is perhaps worth noting that the algorithm proceeds randomly—a typical run calls up about 10 million random numbers—with neither intervention nor the imposition of constraints regarding the shape of the DEM, other than possibly smoothing the running distributions (user’s choice). The only evolutionary imperative is dictated by the single fitness criterion, the chi-squared minimization, obviously much less complex than actual biological evolution, where fitness is not as simply defined.
Our GA code has been tested and performs reliably against both “toy” spectra and spectroscopic data generated at the National Ignition Facility (NIF) at Lawrence Livermore and the OMEGA laser at the Laboratory for Laser Energetics in Rochester, New York. It is not foolproof by any means, but this has more to do with the physics than with the code itself. There is a predilection toward modest degeneracy of adjacent columns of the L matrix. One can invent pathological DEM distributions, say, a triple-delta, that elude the code. This may be ameliorated through the use of L-shell spectra, rather than K-shell spectra. We have begun to explore this conjecture. Nevertheless, tests against real K-shell data from OMEGA buried-layer experiments have shown that the GA code is generally robust, and, in fact, supersedes spectral fitting approaches based on best fits to isothermal models. With further refinements, we plan to increase the versatility and efficiency of the code.
Impact on Mission
Our study into the identification and analysis of temperature gradients in x-ray spectroscopic data supports the Laboratory's high-energy-density science core competency as well as NNSA's goal to strengthen its science, technology, and engineering base.
Conclusion
Although it is only one descriptor, the temperature distribution is an essential feature of the physical state of a laser-produced plasma. We strongly advocate that spectral interpretations accommodate the entire spectrum, rather than individual line ratios, where this latter restrictive view can lead the analyst astray. To achieve this, the multi-thermal DEM approach is necessary. In terms of advancing the state of the code, we have already begun to explore its ability to home in on certain aspects related to radiation transport and emission anisotropy. Another opportunity is to provide a version of the code that can unravel transmission spectra; we are involved in broad-agency collaboration to measure iron opacity on a NIF platform that is currently in development. Again, analogous to the case of emission spectroscopy, without confidence in the temperature distribution, opacity models cannot be subjected to a definitive test. In the shorter term, we plan to apply the GA code to the growing database of experimental x-ray spectra acquired at NIF and OMEGA, which is relevant to Hohlraum Science under the ICF Science Campaigns, and the NLTE program under ICF Integrated Science. We are currently collaborating with experimental teams in these areas. Undoubtedly, we will discover new ideas for expanding the scope of the GA code.
References
Hansen, P. 2010. Discrete Inverse Problems: Insight and Applications. Society for Industrial and Applied MathematicsPhiladelphia, PA.
Hansen, S., et al. 2007. "Hybrid Atomic Models for Spectroscopic Plasma Diagnostics." High Energy Density Physics 3(1–2):109. doi:10.1016/j.hedp.2007.02.032.
Strang, G. 1976. Linear Algebra and its Applications. Academic Press, New York, NY.