Carol Woodward (15-FS-014)
Abstract
Quantitative modeling and simulation of time-evolving natural and engineered systems entails numerically approximating solutions to sets of ordinary or partial differential equations by integrating in time. For many problems of practical interest, different components of the system evolve at different timescales. Examples of such problems occur in plasma physics, molecular dynamics, combustion chemistry, turbulence phenomena, and shock and stellar cluster evolution. To solve these kinds of problems efficiently while resolving relevant physics, one would ideally employ different time steps for different components of the system. To this end, multiple-rate methods were developed. In a fully multi-rate scheme, the integration is asynchronous in the sense that each component of the system evolves using its own time step. Creating a parallel scheme is challenging, because the different components are coupled and need to communicate while never residing at the same moment in simulation time. So far, little work has been done to realize a robust, general, and scalable parallel multirate integrator. Furthermore, most studies of multirate integration have been limited to problems with only a small number of timescales instead of a wide spectrum. We plan to investigate the feasibility of using parallel discrete-event simulation techniques for time integration of large-scale, multi-rate systems of ordinary differential equations of relevance to the DOE. Such capability is crucial to Lawrence Livermore's development of large-scale multiphysics simulations. We will base our proposed multirate integrator on the ROSS (Rensselaer's Optimistic Simulation System) parallel discrete-event simulation code. We will test the feasibility and performance using two problems with multiple and highly localized timescales, and infer from our study the discrete-event simulation of the approach for other applications.
This feasibility study will produce a test-bed code for integrating ordinary differential equations based on discrete-event simulations. The code will then be used to explore the feasibility of using parallel discrete-event simulation approaches for developing scalable, robust multi-rate integrators. If successful, this study will lay the ground work for broader research extending our methods to large-scale complex multiple-physics problems, of interest throughout the DOE applied science and energy community. We expect that the natural feature of a discrete-event process formulation to dynamically limit computational communication will enable this type of integrator to scale better than conventional integrators, which typically rely on standard parallel linear-algebra packages for scalability. The inherent communication sparseness of these multi-rate time integrators makes them well-suited for next-generation supercomputing machines.
Mission Relevance
By providing scalable simulation of systems characterized by a wide spectrum of timescales, parallel discrete-event integrators will enable multiphysics simulation of ever-increasing realism and codes for efficient use of next-generation supercomputers, in support of the Laboratory's core competency in high-performance computing, simulation, and data science.
FY15 Accomplishments and Results
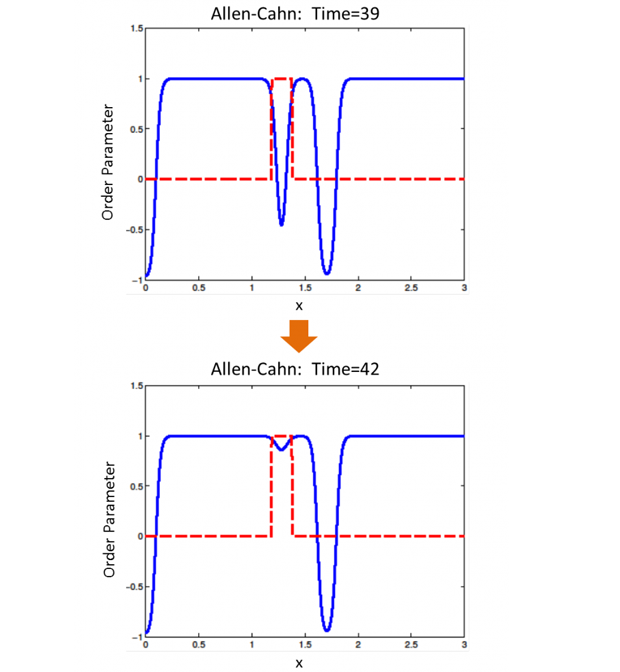
In FY15 we (1) implemented a serial multi-rate time integrator of the second order using several mechanisms for coupling fast and slow timescales; (2) studied the robustness of those integrators on several test problems, including a multi-rate variant of the standard Dahlquist test problem for numerical stability relevant to solving differential equations, an inverter-chain electric network problem relevant to digital electronic-circuit partitioning strategies for numerical simulation packages, a chemical reaction–diffusion problem, an Allen–Cahn equation describing phase transitions for a material contained in a bounded and regular domain, and a combustion chemistry process; and (3) developed a parallel multi-rate integrator based on discrete-event simulation and completed a first test of a parallel ROSS implementation of the method.