Tanya Vassilevska (13-ERD-031)
Abstract
Time-dependent differential equation models of complex physical processes often involve multiple parameters that may be unknown or uncertain. The simulation and analysis of such models is computationally expensive. To enable these computations, we must solve these models faster and use fewer resources. With this project, we focused on the theory and implementation of methods that drastically reduce the amount of computations and memory requirements in solving complex multiphysics problems. We developed a novel adaptive-incremental approach to model reduction that minimizes memory and computational cost requirements, and implemented this approach in a newly developed parallel algorithms library, libRom. This library provides a suite of parallel algorithms for reduced-basis construction and adaptive snapshot sampling from partial differential equation applications. The method was tested on several benchmark problems and demonstrated substantial dimension reduction while maintaining high accuracy and economizing computational cost. The project resulted in novel error bounds providing insight to the source of the reduced-order model (ROM) error for dynamic systems and allowing comparison with a method that augments the solution snapshots with time-derivative snapshots. We compared the accuracy of the two methods and found that, under certain conditions, the method with time-derivative snapshots has better accuracy than the non-augmented one.
Background and Research Objectives
Using ROMs approximates the essential features of complex, large-scale, mathematical models of physical systems. ROMs are designed to be orders-of-magnitude more efficient (in the use of central processing units and memory) than their corresponding high-fidelity models. For example, a single high-fidelity large-eddy simulation of a wind turbine may contain billions of unknowns and take days on a high-performance computer, while a ROM of the same problem would consist of only hundreds or thousands of unknowns and execute in a few seconds on a desktop (or handheld) machine. ROMs are invaluable in applications that require large numbers of simulations such as design optimization, parameter sampling, or rapid evaluation of an engineering model.
Model reduction of time-dependent partial differential equations is based on the idea of semi-discretizing in space the original mathematical model by using cleverly defined basis functions—for example, by using approximations with proper orthogonal decomposition, which is a method of data analysis aimed at obtaining low-dimensional approximate descriptions of high-dimensional processes, used in combination with Galerkin projections for yielding low-dimensional dynamical models.1 The output defines the full-order model, which is then projected in a low-dimensional subspace spanned by a subset of the basis functions (the high-energy modes) to obtain the ROM. Solving the ROM should reduce substantially the memory and computational operations. Importantly, ROMs with proper orthogonal decomposition calculate the reduced-basis functions by using numerical solutions of the full-order model at specific parameter values and time moments (called snapshots). In this way, the basis is adapted to the dynamics of the system. While the methodology of such ROMs is well established, there are outstanding questions that need resolution. The most important goal (and an outstanding question) in this approach is the selection of snapshots so that the ROM error is minimized while maintaining low ROM dimension and also minimizing memory and computational time. The resolution of this question is connected to estimating the ROM approximation error.
Our objectives were to develop (1) ROMs that ran as fast as possible while still retaining an accurate approximation to a given quantity of interest by developing a composite adaptive model characterized by an adaptive optimal snapshot, parameter selection, and incremental basis construction; (2) novel error estimates of the ROM approximation error; and (3) a software framework enabling the entire process of subspace generation, projection, and ROM evaluation.
Scientific Approach and Accomplishments
Limited-Memory Adaptive Snapshot Selection
Our proposed method reduces the offline costs of ROM snapshot selection and basis computation in both memory and floating point operations relative to existing methods in the literature. As such, it minimizes memory requirements for proper orthogonal decomposition algorithms. The novel approach selects snapshots on the fly during solution of the full-order model. Snapshots are selected adaptively in time by calculating the time step between snapshots using methods borrowed from adaptive time stepping for ordinary differential equations. In the adaptive snapshot time-stepping calculation, a low-cost error estimator is used that places no restrictions on the form of the full-order model, in contrast to existing methods that assume the model is a semi-discretized partial differential equation using a specific spatial discretization. As each snapshot is selected, the proper orthogonal decomposition basis is updated using a single-pass incremental singular-value decomposition algorithm developed for streaming data analysis.2 Consequently, only one column of the snapshot matrix must be in memory at any given time, along with the current proper orthogonal decomposition basis matrix. Use of the incremental algorithm for basis computation substantially reduces both memory requirements and the number of arithmetic operations performed by the algorithm, independent of the snapshot selection criterion. The proposed approach also employs no intermediate compression steps. Instead, truncation of the singular-value decomposition algorithm occurs on the fly. After every added snapshot, the truncated incremental algorithm approximates the algorithm that would be obtained from conventional dense singular-value decomposition algorithms. The basic idea of the snapshot-selection algorithm presented is to equally distribute the estimated error without resorting to solving an expensive (in both memory and arithmetic operations) optimization problem.
To our knowledge, this is the first work to propose an inexpensive adaptive method with error control for selecting proper orthogonal decomposition snapshots on the fly using a single pass of a full-order model solution. Furthermore, as far as we know, it is the first work to use single-pass incremental singular-value decomposition methods to append snapshots in time, dramatically reducing the memory footprint of the algorithm for proper orthogonal decomposition and making it more suitable for high-performance computing applications.
When applied to a standard viscous Burgers’ equation benchmark problem from the literature, this adaptive snapshot-selection algorithm gathers no more snapshots than commonly used, equally spaced snapshot-selection algorithms for a given normalized root-mean-square error, at the cost of a slightly larger ROM basis. Independent of snapshot-selection strategy, using an incremental singular-value decomposition algorithm in concert with adaptive snapshot selection drastically reduces memory requirements of proper orthogonal decomposition so that only their basis vectors, their corresponding singular values, and one snapshot must be stored in memory (along with an asymptotically negligible number of additional scalars).
libROM
Overall, one can think of libROM as having two purposes: creation of basis vectors from a simulation, and consumption of those basis vectors to form a ROM. The bulk of the library is devoted to the first of these tasks, while only a small subset is needed to support the second. The libROM library is a collection of C++ programming classes that implements order reduction via singular-value decomposition of sampled-state vectors. Three parallel tests and baseline results are also supplied with the library. The library supports the construction of multiple sets of basis vectors, wherein each set of basis vectors corresponds to a different simulation time interval. Users have control over the maximum number of basis vectors in a set that, along with the adaptive sampling control, determines how many sets of basis vectors will be collected. The library provides the means to read and write the basis vectors resulting from order reduction. Construction of the ROM from the basis vectors must be performed by the application developer and is not a part of the library. The library is configured with a configure script and built with the resulting generated GNU operating system Makefile. There are three required external libraries: mpi, lapack, and hdf5.
Several classes are directly related to the creation of basis vectors. Applications feed state vectors to the library, and basis vectors are the result. In all cases, the algorithms compute the next simulation time at which a sample is needed and are able to answer the query of whether a sample should be taken at a requested simulation time. Two classes, the Static Basis Generator and Incremental Basis Generator wrap a basis vector-creation algorithm with its corresponding sampling algorithm. This provides an application with a single point of interaction should one want to use the library’s sampling algorithms. It is possible for an application to write its own sampling algorithm, in which case it is free to use the basis vector-creation algorithm classes directly instead of one of these wrappers. BasisReader is the one class directly related to the consumption of basis vectors. Its purpose is to allow applications constructing ROMs from basis vectors to read the generated basis vectors corresponding to a specific simulation time. Detailed information about each class is provided in the doxygen (a tool for writing software reference documentation) documentation and the user guide.3 The library enables construction of ROMs for a given application. However, the details of the construction of any specific ROM depends on the nature of the equation being solved.
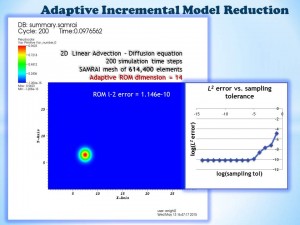
As a demonstration of the capabilities of libROM and the efficiency of the ROM method, we solved an advection–diffusion equation discretized using SAMRAI, a code framework for solving partial differential equations. As shown in Figure 1, the full-order model dimension (number of mesh zones) was 614,400, while the resulting ROM had a dimension of only 14. The L2 norm of the approximation error was extremely small: 1.146 x 10-10. As expected, the magnitude of the error was positively correlated with the sampling tolerance of the adaptive incremental algorithm.
Error Bounds and Analysis
The availability of a priori error estimates or error bounds is important for understanding the origin of the approximation error and controlling it. Although some results on error bounds for ROMs with proper orthogonal decomposition have been published, the bounds rarely contain information about the spacing between snapshots, and none explicitly includes the exact locations of the snapshots. The error bounds we developed are the first to include the time moments of collecting the snapshots, opening the possibility to rationally select these locations while reducing the ROM error.
Most importantly, we compared two ROMs with proper orthogonal decomposition methods for dynamical systems and derived error bounds for both. The first method uses snapshots from the solutions only (standard approach). The second method uses snapshots from both the solutions and their time derivatives. The error bounds in both cases consisted of two terms: one term depending on the largest neglected singular value and the second term depending on the time intervals between consecutive snapshots (but not on the singular value). When the largest neglected singular value is small, the bound of the error depends on the square of the time interval between snapshots for the first method and on the fourth-power of the time interval for the second method. The error bounds suggest that, asymptotically, the ROM method with time-derivative snapshots is expected to have better approximation. Using numerical examples with the FitzHugh–Nagumo equation, we demonstrated that under certain conditions, the method with time-derivative snapshots can yield a significantly smaller error of approximation.
Accomplishments
With the successful conclusion of this project, we developed and tested extensively a novel, computationally inexpensive snapshot-selection method that uses an adaptive time-stepping algorithm with error control to select snapshots on the fly, using a single pass of a full-order model solution.4–6 The method dramatically reduces the memory footprint of the proper-orthogonal-decomposition algorithm to make it more suitable for high-performance computing applications.
In addition, we developed the libROM library of C++ parallel algorithms, which implements order reduction via singular-value decomposition of sampled-state vectors. To calculate the reduced basis, libROM implements two parallel singular-value decomposition algorithms,2 as well as a serial “static” or non-incremental singular-value decomposition algorithm. It also provides a mechanism for adaptive sampling utilizing the error-control adaptive-incremental method.4
Finally, we derived novel bounds of the error for two ROM methods for dynamical systems. The first method is based on collecting snapshots from solutions only, and the second method uses snapshots from both the solutions and their time derivatives. We compared numerically the errors from the two model-reduction methods and investigated the relation between the behavior of the numerically observed error and the error bounds. The error bounds provide insights and justification for using time-derivative snapshots in proper-orthogonal-decomposition model reduction.7,8
Impact on Mission
Our project developed the foundation for enabling effective and fast large-scale multiple-parameter simulations by reliable model reduction. Combining LLNL’s existing simulation expertise based on partial differential equations with a sophisticated ROM infrastructure supports the core competency in high-performance computing, simulation, and data science. The research broadened understanding of ROM’s advantages and disadvantages that need to be addressed for successful applications to a wide variety of computational problems relevant to the Laboratory's mission.
Conclusion
The new computational methods and software library we developed can be used as a component of a procedure for selecting snapshots from simulations of transient full-order models with parameters in order to build ROMs with proper orthogonal decomposition for applications such as optimization, uncertainty quantification, sensitivity analysis, parameter studies, and design of (computational) experiments. However, outstanding issues for successful applications to nonlinear problems do remain and need to be addressed. Specifically, the methods we developed are computationally efficient for linear problems, but more restricted for nonlinear models. A possible path is to adapt our approach for use of the discrete empirical-interpolation method.9 Further, modifying our methods for problems with defined parameters is a necessity. However, questions about the robustness of a reduced basis calculated from a given set of parameters and applied to a broader parameter domain are currently topics of theoretical research where parameter-dependent error estimates need to be established. Work in these areas is of interest to the Department of Defense, for example. Demonstrating successful model reduction of a large LLNL application will open possibilities for further developing the methodology with programmatic and external support.
References
- Kalashnikova, I., and M. F. Barone, "Efficient non-linear proper orthogonal decomposition/Galerkin reduced order models with stable penalty enforcement of boundary conditions." Int. J. Numer. Meth. Eng. 90, 1337 (2012).
- Brand, M., "Incremental singular value decomposition of uncertain data with missing value." Computer Vision ECCV 2002, p. 707 (2002). Springer-Verlag, Berlin, Germany.
- Arrighi W., et al., libROM user guide and design, Version 0.1. (2015). LLNL-SM-674579.
- Oxberry G., et al., Limited-memory adaptive snapshot selection for proper orthogonal decomposition. (2015). LLNL-TR-669265.
- Oxberry G., et al., Parsimonious data acquisition for data-driven model reduction. SIAM Conf. Computational Science and Engineering, Salt Lake City, UT, Mar. 14–18, 2015. LLNL-PRES-668271.
- Oxberry G., et al., Adaptive proper orthogonal decomposition reduced order models via incremental SVD. SIAM Annual meeting, Chicago, IL, July 7–11, 2014. LLNL-PRES-656295.
- Kostova T., et al., Error bounds and analysis of proper orthogonal decomposition model reduction methods using snapshots from the solution and the time derivatives. (2015). LLNL-JRNL-663838. arXiv:1501.02004v1
- Kostova-Vassilevska, T., et al., Using snapshots of the derivatives in proper orthogonal decomposition—Based reduced order methods for dynamical systems. 2014 SIAM Ann. Mtg., Chicago, IL, July 7–11, 2014. LLNL-PRES-656417.
- Chaturantabut, S., and D. C. Sorensen, "Nonlinear model reduction via discrete empirical interpolation." SIAM J. Sci. Comput. 32(5), 2737 (2010).
Publications and Presentations
- Arrighi, W., et al., libROM user guide and design. (2015). LLNL-SM-674579.
- Kostova T., et al., Error bounds and analysis of proper orthogonal decomposition model reduction methods using snapshots from the solution and the time derivatives. (2015). LLNL-JRNL-663838. arXiv:1501.02004v1
- Kostova-Vassilevska, T., et al., Using snapshots of the derivatives in proper orthogonal decomposition—Based reduced order methods for dynamical systems. 2014 SIAM Ann. Mtg., Chicago, IL, July 7–11, 2014. LLNL-PRES-656417.
- Oxberry G., et al., Adaptive proper orthogonal decomposition reduced order models via incremental SVD. SIAM Ann. Mtg., Chicago, IL, July 7–11, 2014. LLNL-PRES-656295.
- Oxberry G., et al., Limited-memory adaptive snapshot selection for proper orthogonal decomposition. (2015). LLNL-TR-669265.
- Oxberry G., et al., Parsimonious data acquisition for data-driven model reduction. SIAM Conf. Computational Science and Engineering, Salt Lake City, UT, Mar. 14–18, 2015. LLNL-PRES-668271.