1. Home
  2. Report Archives
  3. FY2016
  4. High-Performance Computing, Simulation, and Data Science
  5. A Coupled Seismic and Acoustic Simulation Capability

A Coupled Seismic and Acoustic Simulation Capability

Arthur Rodgers (14-ERD-001)

Abstract

Many natural and man-made events of interest, such as earthquakes and explosions, occur near or above the interface between the air, water, and solid earth. However, there were no tools that allowed the joint modeling of acoustic and seismic signatures from these events—. For this project, we developed a coupled seismoacoustic simulation capability to model mechanical waves in the atmosphere and the solid earth with three-dimensional heterogeneous properties and non-planar surface topography. In EIAc, our seismoacoustic parallel computer code, the solid earth seismic wave propagation method closely follows Livermore's three-dimensional seismic modeling code, SW4, and includes all features needed for realistic seismic wave simulations. Waves in the atmosphere are modeled assuming linearized Euler equations for a compressible, possibly moving, fluid. The atmosphere is represented with realistic three-dimensional variations in pressure, temperature, and winds, which impact the traveling sound waves. Energy flows between the atmosphere and solid earth by imposing the boundary conditions at the possibly non-planar interface representing surface topography. A curvilinear mesh is used to discretize the region near the non-planar interface. The numerical scheme for solving the equations of motions is based on summation-by-parts. The major contributions of this research are (1) a generalization of the summation-by-parts technique to the coupled fluid-solid interface with the same strong numerical stability properties as SW4, and (2) a new method for discretizing point sources in a fluid. This code has applications to modeling mechanical waves from energetic events both natural (e.g., earthquakes and bolides—large meteors that explode in the atmosphere) and man-made (e.g., explosions and collapses). Additionally, a two-dimensional acoustic wave propagation code, AC2D, was developed that solves a two-dimensional version of the same linearized Euler equations as ElAc and has applications to long-range sound propagation where three-dimensional calculations are still prohibitively expensive. Both computer codes are now being used in direct-funded projects.

Background and Research Objectives

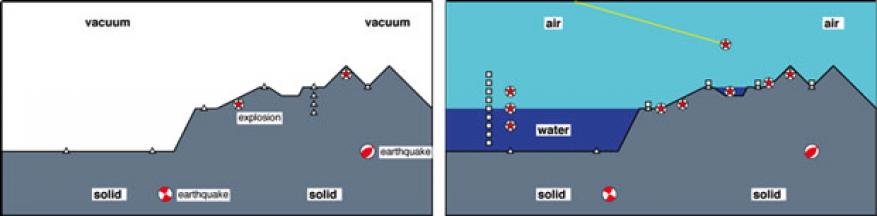
Seismic and acoustic waves are key observables for understanding natural and man-made energetic events. These disturbances are sources of mechanical motions that travel through the solid earth as seismic waves and through the atmosphere as acoustic waves. For events near the earth’s surface it is often possible to observe both seismic and acoustic waves because of coupling of motions between the atmosphere and solid earth. These waves allow remote detection and characterization of the source and/or constraints of the media through which they travel. Recently, the term seismoacoustics has been used to describe the emerging field of study of such coupled waves traveling in the solid earth and atmosphere.1 Because acoustic waves in the atmosphere generally travel slower than seismic waves in the solid earth, these phenomena often separate, especially far from the source. However, near the source or where seismic and acoustic waves convert from one form to another, such as where seismic wave speeds are comparable to acoustic wavespeeds, the coupling of seismic and acoustic energy must be included for accurate representation of the wavefield. Figure 1 (right) illustrates some of the phenomena that can be considered in seismoacoustics and demonstrates some of the phenomena we sought to model with our new ElAc simulation code.


Figure 1. (left) the sw4 seismic simulation capability models elastic motions in the solid earth while treating the air as a vacuum. (right) eiac can model a range of phenomena important to seismoacoustics. the ability of elac to model waves in the water has not been fully explored.
Figure 1. (left) The SW4 seismic simulation capability models elastic motions in the solid earth while treating the air as a vacuum. (right) EIAc can model a range of phenomena important to seismoacoustics. The ability of ElAc to model waves in the water has not been fully explored.

Our project extends the tremendous utility of SW4.2 While there are numerous methods and some open-source computer codes for modeling seismic wave propagation, we know of only a few examples of simulation of coupled three-dimensional seismoacoustic phenomena. These examples use the spectral element method and require building and verifying a mesh, which can be a time-consuming and error-prone process. As of this writing, we know of no open-source code for parallel, coupled, three-dimensional, seismoacoustic simulation with a moving atmosphere and surface topography. ElAc automatically generates its structured Cartesian mesh and curvilinear mesh near the topographic interface, similar to SW4, greatly facilitating applications to problems.

Our coupled seismoacoustic simulation code fills a gap in existing capabilities. In recent years LLNL programs have found the need to model atmospheric overpressure from explosions for the purposes of nuclear forensics and explosion monitoring. During the course of this project, we applied ElAc to model acoustic signals from explosions. The effects of wave propagation in realistic atmospheric structure, including variations in sound speed and wind, must be accounted for in order to isolate source properties. Having a simulation capability allows us to investigate source and propagation effects in controlled experiments on Livermore's world-class computers, without having to undertake expensive experiments.

Scientific Approach and Accomplishments

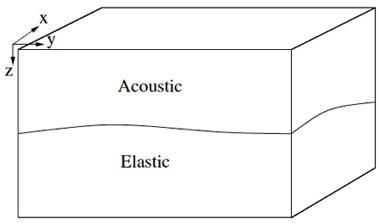
Development of ElAc required theoretical analysis for sound propagation in the atmosphere and treatment of the boundary conditions and energy flow across a possibly non-planar topographic fluid–solid interface as well as source discretization.3,4 Figure 2 shows the domain for EIAc's seismoacoustic simulations.

Figure 2. schematic of the domains considered in elac’s seismoacoustic simulations. an acoustic domain, such as the atmosphere, overlays an elastic domain, such as the solid earth. the two domains are in contact along a possibly non-planar topographic interface.
Figure 2. Schematic of the domains considered in ElAc’s seismoacoustic simulations. An acoustic domain, such as the atmosphere, overlays an elastic domain, such as the solid earth. The two domains are in contact along a possibly non-planar topographic interface.

Because we sometimes want to model only acoustic propagation, ElAc may optionally be run without seismic propagation, in which case the interface reflects sound back into the acoustic domain. Methods for acoustic wave propagation have been developed in three dimensions.5,6

Theoretical work started with the equations governing acoustic propagation in the fluid atmosphere, beginning with the Navier-Stokes equations for fluid flow. Wave motion is considered a small perturbation to large-scale flow of the atmosphere. It is well known that wind plays an important role in sound propagation, and we considered it a requirement that ElAc should include wind effects.

Proper treatment of the boundary conditions between fluid and solid—so that energy could flow from the fluid to solid and solid to fluid—was accomplished by imposing the continuity of the normal component of the velocity and stresses. The elastic wave solver in the solid earth, taken as SW4, uses fourth-order accurate solution and second-order boundary modifications for overall fourth-order accuracy. To maintain fourth-order accuracy for ElAc, we discretized the acoustic domain with sixth-order accuracy with third-order modifications at the boundary, maintaining overall fourth-order accuracy in the solution. Numerical experiments to measure the convergence rate of the code using the method of manufactured solutions demonstrated that the elastic and acoustic domains showed fourth-order convergence measured in L2 norm. However, the acoustic domain for atmospheric sound propagation showed a slightly less than fourth-order convergence in maximum norm.3

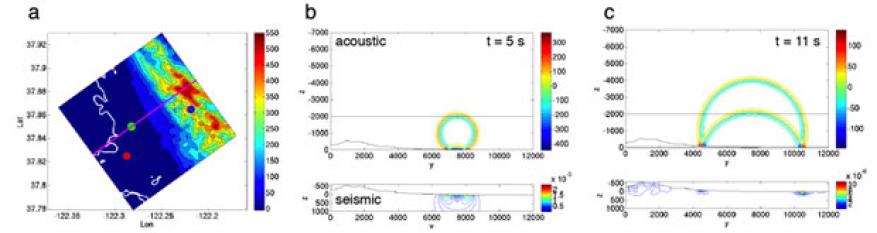
Figure 3 illustrates coupled seismoacoustic wave propagation for an explosion in the atmosphere above Berkeley, California.3 In this example, acoustic waves from the source in the air strike the solid earth and generate seismic waves, which travel faster than the acoustic waves, as shown in Figure 3(b). As the acoustic wave spreads along the earth’s surface it continuously generates seismic waves, as shown in Figure 3(c).


Figure 3. illustration of coupled seismoacoustic wave propagation. (a) the computational domain shows surface topography, the location of the source (green dot) and the line where vertical cross-sections are plotted. (b, c) acoustic (upper) and seismic (lower) wave motions at time t = 5 s and 11 s, respectively.
Figure 3. Illustration of coupled seismoacoustic wave propagation. (a) The computational domain shows surface topography, the location of the source (green dot) and the line where vertical cross-sections are plotted. (b, c) Acoustic (upper) and seismic (lower) wave motions at time t = 5 s and 11 s, respectively.
 

The ElAc code was applied to account for acoustic propagation effects in explosive energy release (yield) estimation. Green's functions for sound propagation based on measured atmospheric structure were computed with ElAc. This allows the estimation of the pressure time-history at the source, which can be related to yield. Under direct program funding, we used ElAc to estimate yields of large chemical high-explosive experiments conducted by the Defense Threat Reduction Agency.5

Impact on Mission

Our research will enable understanding of seismic and acoustic propagation effects that bias source estimates with the development of a simulation capability that is compatible with Laboratory hydrodynamic codes. This capability falls within the Laboratory's core competency in high-performance computing, simulation, and data science. This foundational science is supportive of critical mission needs such as intelligence for nuclear nonproliferation to monitor nuclear explosions, national security to determine the defeat of hard and deeply buried targets, and new ways to extract underground energy more efficiently while minimizing risk and environmental impact.

Conclusion

For this project we developed the ElAc, a new parallel simulation code for coupled seismoacoustic wave propagation in three dimensions. With EIAc, we now have the necessary capability to model acoustic and coupled seismoacoustic waves. The code is based on substantial theoretical development to model acoustic propagation with the summation-by-parts principal in a realistic atmosphere (with wind), accurate treatment of the motions at a non-planar topographic interface separating the fluid and solid and proper discretization of the source. The code could be distributed as open-source, similar to SW4, and will likely be used by scientists and engineers interested in the wide array of applications where waves are present at solid–fluid boundaries. These applications may highlight needs for further development and/or features to improve coupled seismoacoustic or acoustic-only simulations. ElAc has been used to compute Green’s functions for a new explosion yield estimation method and is written into plans for our NNSA Defense Nuclear Nonproliferation Research and Development Nuclear Forensics Venture (F-2016) life cycle plan. During our three-year project, there was also interest in modeling acoustic signals generated by underground explosions and comparing with experimental data from the Source Physics Experiment, which is a series of buried fully tamped chemical high-explosive experiments at the Nevada National Security Site. Another related new program, Low Yield Nuclear Monitoring, is currently being scoped and also includes applications of ElAc.

In another project accomplishment, new early career geophysicist Dr. Keehoon Kim developed a new two-dimensional acoustic wave propagation code (AC2D), which was not in the original planned scope, but was accomplished in addition to EIAc. Subsequently, Dr. Kim worked with the project PI on directly funded applications of ElAc for modeling acoustic waves from explosions, efforts that attracted future directly funded work to support nuclear forensics as well as the Source Physics Experiment and Low Yield Nuclear Monitoring programs. It is possible that AC2D could be used for long-range acoustic simulations supporting forensic analyses of explosions at longer range (hundreds of kilometers or more) or other energetic sources (e.g., volcanoes and meteor explosions).

References

  1. Arrowsmith, S. J., et al., "The seismoacoustic wavefield: A new paradigm in studying geophysical phenomena." Rev. Geophys. 48(4), RG4003 (2010). http://dx.doi.org/10.1029/2010RG000335
  2. Petersson, N. A., B. Sjogreen, and A. J. Rodgers, A seismo-acoustic infrasound methodology for accurate large scale simulations. Seismological Society of America Ann. Mtg., Anchorage, AK, Apr. 29–May 2, 2014. LLNL-ABS-648056.
  3. Petersson, N. A., and B. Sjogreen, High order accurate finite difference modeling of seismoacoustic wave propagation in a moving atmosphere and a heterogeneous earth model coupled across a realistic topography. (2016). LLNL-JRNL-704612.
  4. Petersson, N. A., et al., "Discretizing singular point sources in hyperbolic wave propagation problems." J. Comp. Phys. 321, 532 (2016). LLNL-JRNL-679293. http://dx.doi.org/10.1016/j.jcp.2016.05.060
  5. Ostashev, V. E., et al., "Equations for finite-difference, time-domain simulation of sound propagation in moving inhomogeneous media and numerical implementation." J. Acoust. Soc. Am. 117(2), 503 (2005). http://dx.doi.org/10.1121/1.1841531
  6. de Groot-Hedlin, C., M. Hedlin, and K. Walker, "Finite difference synthesis of infrasound propagation through a windy, viscous atmosphere: application to a bolide explosion detected by seismic networks." Geophys. J. Int. 185(1), 305 (2011). https://academic.oup.com/gji/article/185/1/305/602505
  7. Kim, K., and A. J. Rodgers, "Waveform inversion of acoustic waves for explosion yield estimation." Geophys. Res. Lett. 43(13), 6883 (2016). LLNL-JRNL-689057. http://dx.doi.org/10.1002/2016GL069624
  8. Kim, K., N. A. Petersson, and A. J. Rodgers, Acoustic wave propagation modeling by 2-D finite-difference summation-by-parts algorithm. (2016). LLNL-TR-706674.
  9. Kim, K., and A. J. Rodgers, Explosive yield estimation from acoustic waveform inversion including three-dimensional propagation effects. Seismological Society of America 2016 Ann. Mtg., Reno, NV, Apr. 20–22, 2016. LLNL-ABS-680519.

Publications and Presentations

  • Kim, K., and A. J. Rodgers, Acoustic full waveform inversion to characterize near-surface chemical explosions. American Geophysical Union Fall Mtg., San Francisco, CA, Dec. 14–18, 2015. LLNL-ABS-675516.
  • Kim, K., and A. J. Rodgers, "Waveform inversion of acoustic waves for explosion yield estimation." Geophys. Res. Lett. 43(13), 6883 (2016). LLNL-JRNL-689057. http://dx.doi.org/10.1002/2016GL069624
  • Kim, K., et al., 3D finite-difference time-domain simulation of explosion infrasound in rough topography. Infrasound Technology Workshop, Vienna, Austria, Oct. 15–19, 2015. LLNL-ABS-674228.
  • Petersson, N. A., et al., "Discretizing singular point sources in hyperbolic wave propagation problems." J. Comp. Phys. 321, 532 (2016). LLNL-JRNL-679293. http://dx.doi.org/10.1016/j.jcp.2016.05.060
  • Rodgers, A. J., Infrasound from buried seismic sources in the presence of surface topography. 166th Acoustical Society of America, San Francisco, CA, Dec. 2–6, 2013. LLNL-ABS-640179.
  • Rodgers, A. J., Synthesis of acoustic signals from buried seismic sources in the presence of surface topography. American Geophysical Union Fall Mtg., San Francisco, CA, Dec. 9–13, 2013. LLNL-ABS-641587.
  • Rodgers, A. J., B. Sjogreen, and N. A. Petersson (2015). Simulation of coupled seismoacoustic wave propagation in three-dimensions with a summation-by-parts finite difference method. Seismological Society of America Ann. Mtg., Pasadena, CA, Apr. 21–23, 2015. LLNL-ABS-665932.
  • Sjogreen, B., and N. A. Petersson, “Summation by parts finite difference approximations for seismic and seismo-acoustic computations.” Proc. Intl. Conf. Spectral and High Order Methods, Springer, New York, NY (2015). LLNL-PROC-659087.
  • Sjogreen, B., and N. A. Petersson, User's guide to ElAc, version 1.0. (2016). LLNL-SM-704300.