Andris Dimits (15-ERD-059)
Abstract
The objective of this project was to develop an efficient scheme to couple kinetic Monte Carlo (MC) neutral species and fluid plasma (charged) species codes for the simulation of transport in the outer edge region of magnetic fusion energy (MFE) edge simulation. There was a need for improvement over existing plasma-neutral transport codes, which are either all-fluid and insufficiently accurate in some important regimes, or very slow due to their use of simple explicit (operator split) coupling. The resulting capability creates great value in the interpretation and design of present-day and future MFE plasma devices (e.g., the International Thermonuclear Experimental Reactor or ITER). We developed and demonstrated several new algorithms that greatly accelerate coupling between numerical code or model components where the coupling introduces numerical “stiffness” and where there is an MC component. Some of these algorithmic components have been implemented in our application code, which is a combination of the UEDGE plasma transport module and the DEGAS-2 neutral species kinetic MC transport code. Furthermore, our investigations suggest a clear development “path of least resistance” for further improvement. Though we did encounter a serious challenge, namely a larger-than-expected effect of MC noise on the numerical convergence and accuracy, we quantified the problem and found solutions, some of which pre-existed in mathematical literature; others we developed ourselves. Additionally, we made upgrades to UEDGE and its coupling to DEGAS-2 (a Monte Carlo code for studying neutral transport in plasma) that make it more attractive to other researchers and will enhance its appeal as a tool for physics and design studies.
Background and Research Objectives
Self-consistent predictive modeling (i.e., modeling where the plasma and neutral species are self-consistently coupled) of plasma transport and neutral particle species—and of energy in the edge plasma—has been recognized as essential to the performance of present-day and future MFE burning plasma devices (FESAC 2014; ReNEW 2009).
At the beginning of the project, there was a need for improvement over existing plasma-neutral transport codes, which are either all-fluid and insufficiently accurate in some important regimes, or very slow (Kukushin 2011), due to their use of simple explicit (operator split) coupling. The success of the all-fluid UEDGE code—due in significant part to its advanced algorithms—strongly suggested that better algorithms were possible to greatly speed up the coupling to a kinetic neutrals code (Rognlien 2002). Such capability would be a significant advance for the interpretation and design of present-day and future MFE plasma devices such as ITER.
Scientific Approach and Accomplishments
We adopted a multi-pronged approach for understanding the mathematical and computational issues associated with the coupling problem, developing and testing new algorithms and implementing them in our primary application code combination.
To develop an understanding of key algorithmic tools, issues, and relationships, we used mathematical analysis and “testbed” codes, which are user-friendly implementations of problems that are simplified versions of the full transport application, but which retain the same mathematical and computational challenges. This approach has been applied to investigate nonlinear solvers—Jacobian-free Newton-Krylov (JFNK), quasi-Newton methods such as Broyden’s methods, and fixed-point iteration—to develop and customize preconditioners based on state of the art methods.
After gaining an understanding of these methods via analysis and testbed code studies, we implemented methods found to be useful in the application-code coupling of the UEDGE and DEGAS-2 codes. We then verified the new coupled-code combination against the existing explicit coupling. Some validation was provided through validation exercises that were done with the pre-existing code coupling, and additional validation was done and will likely continue as part of follow on programmatic work.
In the process of developing the new algorithms and methods, we drew on examples from other fields, such as radiation and neutron transport. These served as models that are relevant to, but simpler than the neutral-species problem of providing more readily verifiable test cases, such as in the development and demonstration of the efficacy of fluid/moment model-based preconditioners. These also serve as examples that demonstrated the relevance of our algorithms to these other fields.
During this project, we investigated a logical sequence of algorithmic issues and undertook code-development tasks. These included the following: (1) time scale quantification involved in the physical system, (2) stability limits, (3) local convergence rates, (4) global convergence, and (5) errors of particular schemes as a function of parameters, both physical (e.g., heat flux entering the scrape-off layer region from the core) and numerical (e.g., the time step mesh sizes, and MC particle number), (6) implementation of algorithmic components in the application code, (7) verification, (8) performance tuning, and (9) validation.
Summary of Results
We developed several new algorithms for our UEDGE–DEGAS-2 code coupling. Some were proven to achieve excellent convergence in a coupled combination of nonlinear fluid plasma and kinetic neutrals models including both deterministic and MC solution methods of the kinetic model. A key challenge was the noise introduced into the coupled simulation by the MC neutrals component. We tested portions of a strategy in the applied mathematics literature (Willert 2015) for optimizing a JFNK method in the presence of MC noise and found that it is a viable way forward for the plasma neutrals transport problem that was the target of this project. We also identified a staged implementation path that achieved significant benefits over explicit coupling with only parts of the overall scheme outlined there.
In addition to our plasma neutrals problem, we made progress in other mission-relevant fields such as radiation and neutron transport. In particular, we found that a simple forward Euler pseudo time-stepping or relaxed fixed-point iteration approach gives excellent convergence rates if the function where it is applied is well preconditioned. Furthermore, we showed that an approximate inverse of the Jacobian for the diffusive-regime moment (fluid) model provides an excellent—in a sense that we quantify—preconditioner for the kinetic problem across regimes.
In the process of implementing portions of the coupling algorithms, we modernized the UEDGE code and its coupling to the DEGAS-2 neutrals code in ways that we expect will significantly enhance the appeal and longevity of UEDGE—both as a standalone research code and as a coupled-code component.
We also carried out significant investigations to understand and map out parameter regimes in which the coupled transport problem—handled with explicit coupling—is numerically stable or unstable due to stiffness in the coupling (as opposed to explicitness in the stepping or iterations in the solution of the separate models).
Stability of Explicit Coupling
We conducted many analyses of the numerical stability of explicit coupling. In so doing, we worked out a general formal description of the coupled plasma–neutral evolving transport to help solve steady-state problems. The most straightforward implicit scheme—which is used by UEDGE—views the whole numerical plasma–neutrals state as one big vector that evolves according to an equally large vector function and obtains the solution (e.g., a steady state) via one or many backward Euler steps using a nonlinear solver. This is referred to as the “full problem.” This problem is often the basis for coupling pre-existing codes that solve some part of the whole system of interest, and is the underlying basis of much of our algorithmic development work. A way to modularize the problem is to recast it as a “constrained problem.” Here, the state vector and function components are split into two—one for the plasma and one for the neutrals, and then the solution is viewed for one component—the neutrals—as having an instantaneous dependence on the other—the plasma—via a constraint.
For the constrained problem formulation, we derived general relations between the Jacobian (first variational derivative) of various stepping or iteration schemes to that of the continuous-in-time problem, and then we came up with a formal stability criterion—both as a time-step-dependent and as an unconditional stability/instability boundary. Schematically, this criterion shows that the explicit coupling can become unstable when the coupling between the plasma or neutral species/models is strong, and if there are slow rates (e.g., global transport rates) for the species models individually. As expected, if the system is physically stable (i.e, stable in the small-time-step limit), then the implicit backward Euler coupled step is unconditionally stable.
We gained an excellent understanding for the behavior of these criteria via our testbed codes for coupled two-species (plasma and neutral) represented by either diffusion or two-moment models in cases where the background equilibrium was uniform. In these cases, the stability criteria was obtained analytically, and we carried out detailed comparisons of these analytical results against testbed-code computations. In more realistic cases, where the equilibria are nonuniform, it is sometimes possible to calculate the equilibria analytically, but in general not the stability criteria. For some such cases, we mapped out the stability criteria numerically using the testbed codes.
Preconditioners
The convergence rate of many iterative schemes is fast or slow if a parameter called the “condition number” (basically the ratio of largest to smallest eigenvalues of its iteration Jacobian matrix) is respectively small—close to unity—or large. “Preconditioning” is therefore a key method for accelerating iterative schemes, and can be thought of as transforming the function that is iterated to find the solution so that its Jacobian is close to unity. It can enhance the convergence rate of many common iterative schemes including JFNK methods and for Broyden’s methods (Kelley 1995). It is worth noting that even a very crude approximation to the inverse Jacobian may serve as an excellent preconditioner.
A valuable finding was that preconditioning can also greatly enhance the convergence rate of simple explicit methods such as forward Euler and fixed-point iteration with relaxation. This provides the simplest path forward for coupling involving an MC component, as elaborated below.
We developed a way to “extract” the appropriate preconditioner for the constrained problem from one that has been obtained for the full problem. This was especially useful for our work because UEDGE already has excellent full-problem preconditioner implementations that this result enables us to use for the coupling problem.
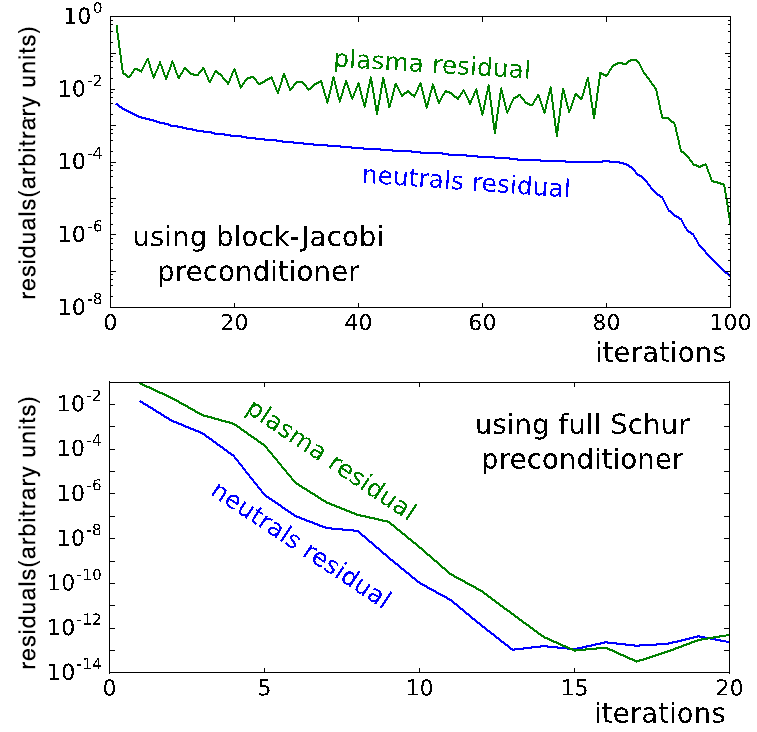
Figure 1 shows the improvement in the convergence rate from a preconditioned constrained problem plasma function obtained by constructing an incomplete lower upper decomposition with a threshold (ILUT) preconditioner for the full system. For this test case, the plasma-neutral system was represented by a non-linearly coupled set of diffusion equations.
A key consideration was the need for the preconditioner to be good when there was a kinetic component in the problem, as there was for the neutral species in our case. Obtaining the Jacobian by direct numerical variation from the full kinetic problem was typically computationally prohibitive for realistic simulations, and a potentially attractive strategy for “building” a preconditioner was to base it on a fluid model. However, there was no guarantee in general that a fluid model was a sufficiently good approximation to the kinetic one. We carried out analytical investigations of simple kinetic models, including a paradigm single-speed radiation transport problem, and found that an approximate inverse Jacobian for a diffusion-approximation moment model could be an excellent preconditioner for the full kinetic problem across all regimes, and could reduce the condition number of the resulting problem from one that is very large to a number of order 2. This suggested that for kinetic problems, sensible moment/fluid model-based preconditioners may provide excellent convergence acceleration.
Testbed Investigations of Implicit Coupling of Fluid Plasma and MC Neutrals
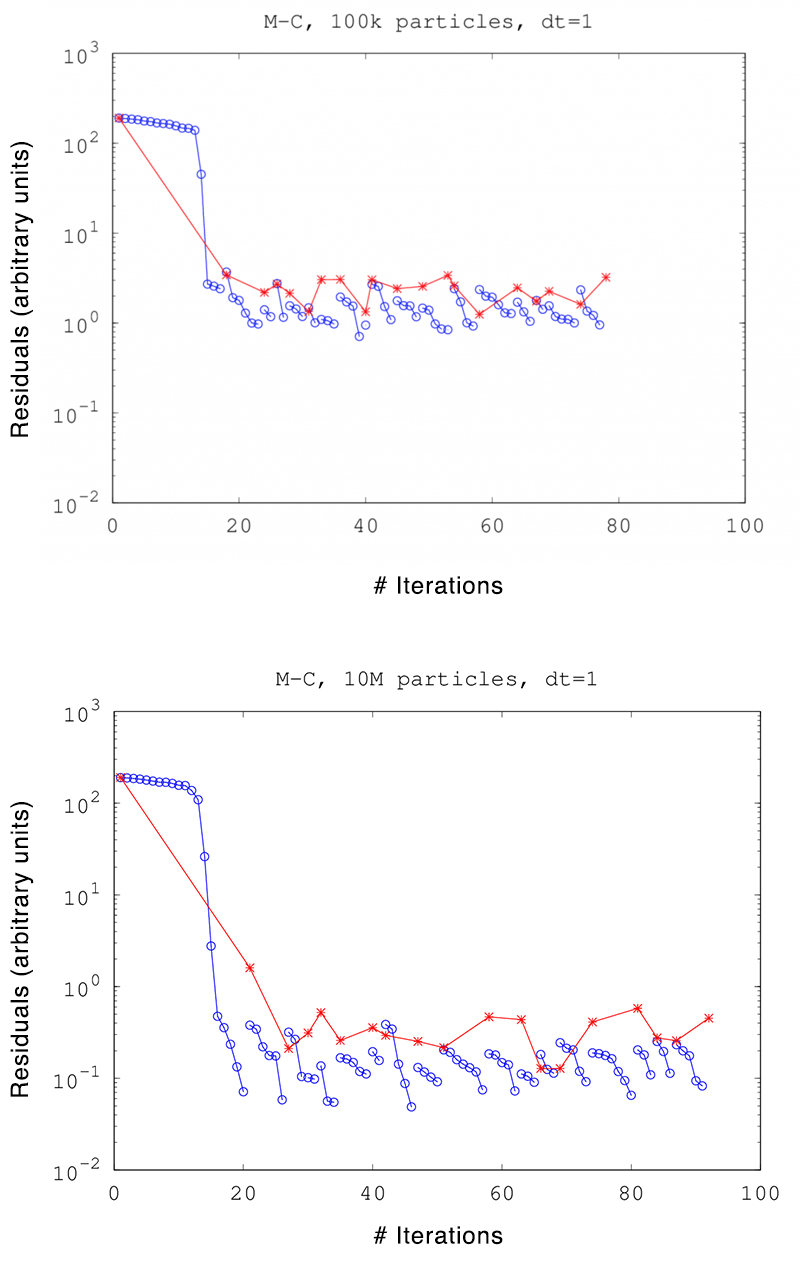
We investigated JFNK for a one-dimensional coupled MC neutrals and fluid plasma model in a testbed code. The physical model was such that the Jacobian was known analytically, so an MC-based Jacobian vector product calculation was not needed, unlike for a more complete and accurate kinetic neutral model. Good convergence could be achieved if, in addition, the Jacobian had a moderate condition number. Figure 2 shows the residuals for these calculations and for particles. The calculations reach their asymptotic residual within a few nonlinear iterations. The early nonlinear iterations had approximately 10–20 linear Krylov iterations, while the later ones typically had of order 5.
Investigations with UEDGE and DEGAS-2
We set up and reproduced simulations of a “box geometry” case (Rensink 1998) using explicit couplings of the UEDGE fluid plasma and neutral species models, and of coupled UEDGE fluid plasma and DEGAS-2 kinetic MC neutrals models. The fastest time scales in a nominal box geometry case were found to be associated with the charge exchange, while the slowest rates were associated with global particle balance and transport in the presence of strong recycling.
This case, when run with explicit coupling, could become unstable for a sufficiently large time step of the simulation using DEGAS-2 and using the UEDGE fluid neutrals model. An important parameter was the “input power” (i.e., the power flow into the simulation volume that represented power coming from the core region). For sufficiently large power, the plasma behavior was robust and there was no time step stability threshold. As the power was reduced, the plasma became “detached” from the “target plate.” In this state, the heat flow largely did not reach the plate via the plasma. Instead, the power radiated, and in some cases, there was a region of very low plasma density and high neutral density near the plate. The detached state and its (physical) stability were of great interest because in it, the damage to the plate and associated contamination of the plasma could be greatly minimized. Unfortunately, it was in this state and in the regime of input power where the transition occurred and where the explicit coupling encountered the restrictive time-step threshold.
A more detailed understanding of the numerical instability associated with explicit coupling and its physical and numerical parameter dependences was obtained with one-dimensional simulations using explicit couplings of the UEDGE fluid models and of the UEDGE plasma model with a simplified one-dimensional kinetic-neutrals model.
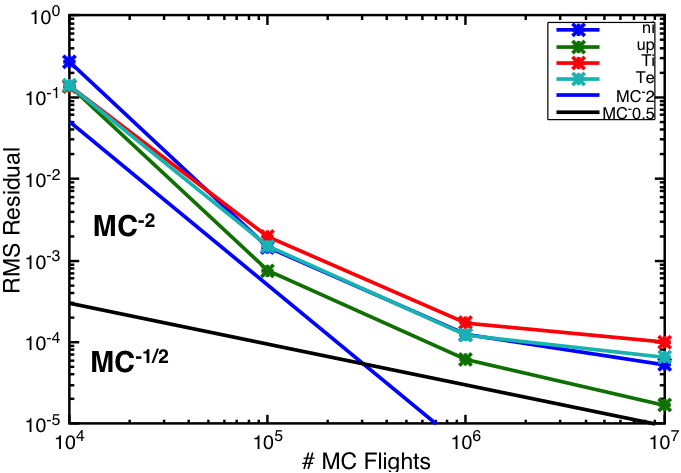
Convergence of coupled UEDGE and DEGAS-2 runs with a MC particle number was carefully investigated using box-geometry cases (Joseph 2017). Figure 3 shows the root mean square (RMS) residuals versus the number of MC flights for this case. A significant range exists where improvement in convergence scales much more than MC-1/2 indicated that nonlinear bias errors play a significant role.
Our first implementation of implicit coupling for the UEDGE and DEGAS-2 combination used the JFNK algorithms and coding already present in UEDGE for its fully implicit solvers. It was found that for this implementation, there was no convergence towards a solution at all unless the time steps were very small. This finding presented us with an obstacle and it was determined that the likely cause was the use of the default method for calculation of the Jacobian vector product in the linear Krylov iterations of the JFNK method via very small finite differences. As had been previously noted (Kelley 2013), this approach failed when there was a MC component in the simulation. We found several alternative approaches that addressed this issue, which are discussed below.
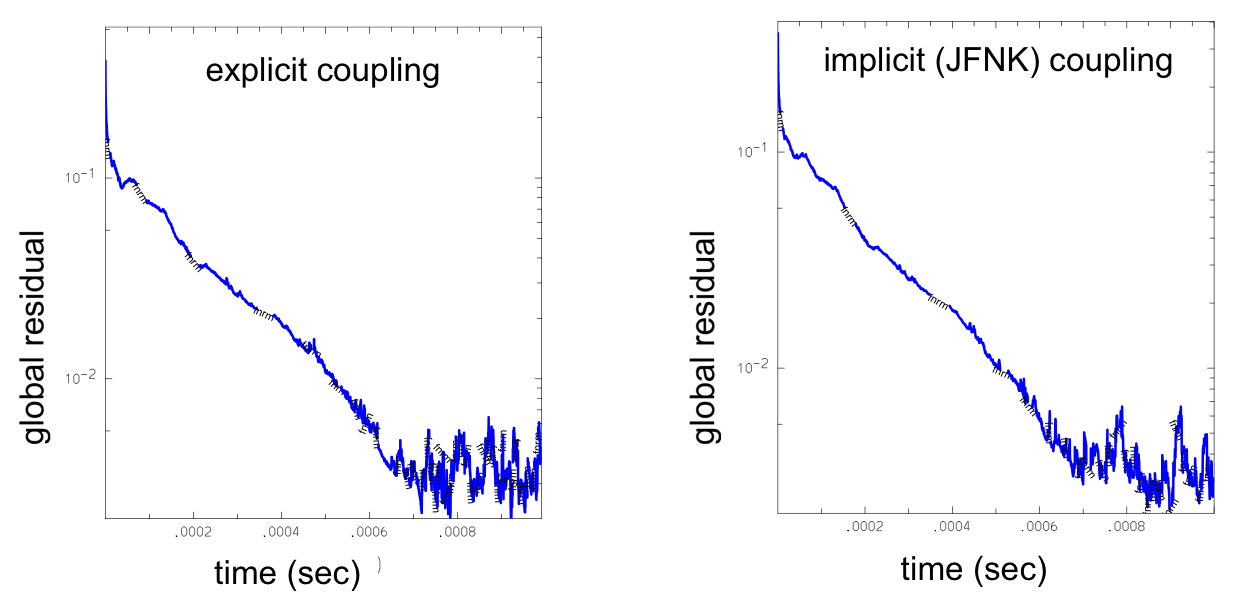
We verified the implicit coupling implementation against the pre-existing explicit one. Figure 4 shows excellent agreement in a comparison of global residuals for explicit and implicit coupling runs of a box geometry case run with very small time steps.
While validation was provided indirectly through verification of the coupled code against previous validated cases, we worked on further validation for DIII-D coupled runs, extending previous work by Rensink.
Advanced Algorithms to Optimize Coupled Solution in the Presence of MC Noise
The first approach we investigated (as had others, e.g., Dekeyser 2014) was “correlated sampling” in the MC (neutrals) calculation. Here, all random number seeds in the MC calculation are controlled so that the calculation becomes deterministic, at least near convergence. The difference-calculation problem for the Jacobian vector product might then be eliminated. However, collective investigations (Dekeyser 2014) have found that the correlated-sampling state can be very difficult to achieve for cases with significant neutral density, with more than one spatial dimension, and with good resolution. We decided this was not a reliable approach for difficult cases of practical interest. Furthermore, the resulting converged solution for a given particle number is still no more accurate than it would be for a converged calculation with the same particle number done with random (non-correlated) sampling.
A more promising and likely more robust approach is an extension of JFNK to problems with a MC component (Kelley 2013; Willert 2015). Here, we give a brief summary of the key ingredients. These apply in a closely related way to Broyden’s methods as well.
The first requirement was an approximation to the Jacobian vector product that has sufficient accuracy. This accuracy can be fixed (e.g., calculated using a fixed number of MC flights), but needs to be sufficiently close to achieve any convergence at all, instead of non-convergence.
Kelley and Willert pointed out that the typical default finite-difference calculation should not be used. For very small difference intervals, such a calculation would be completely dominated by noise. Even if the difference increment could be optimized, such a calculation could only be a convergence rate with a particle number that is significantly slower than the “standard” MC error scaling. Kelley also noted that it is usually possible to calculate the Jacobian vector products with a direct analytical–MC procedure, which recovers the “standard” MC error scaling, and which we have customized for our problem.
In the second requirement, the final accuracy of the solution is tied irreducibly to the accuracy with which the right-hand side function is evaluated. This evaluation was best done with exponentially increasing MC particle numbers, and therefore, accuracy. By focusing the bulk of the computational effort in the late iterations, the greatest accuracy of the solution possible was achieved. Importantly, nonlinear bias errors were minimized by this approach.
A third requirement is a very good preconditioner to minimize the number of linear Krylov iterations between Newton steps. This helps greatly with convergence and enables focusing the vast bulk of the computational work on very accurate, large MC particle-number calculations of the RHS function in the late stages of the solution. We developed very promising preconditioner methods for our problem, as discussed above.
Given that all the major iterative linear and nonlinear solution schemes depend heavily on preconditioning, we realized that very significant acceleration of explicit schemes, including implicit coupling schemes (e.g., forward Euler steps), can also be achieved by suitable preconditioning. This was demonstrated on a relevant nonlinear diffusion model of the plasma with a fixed neutral background. We expect that this will achieve the bulk of the convergence-rate speedup that is possible for an implicit UEDGE and DEGAS-2 coupling, and will result in a major advance in capability.
More sophisticated solution schemes, such as advanced explicit schemes, the JFNK approach of Kelley and Willert, and similar approaches based on Broyden’s methods, may still have advantages but should probably be viewed as refinements.
Code Modernization
Our research also resulted in progress on a Python version of UEDGE and its framework for coupling with DEGAS-2. The importance of this to our project was we wanted UEDGE, including the components we developed for the coupling to DEGAS-2, to be an attractive tool for early-career and senior researchers, both outside and within the Laboratory. The current mainstream UEDGE version is used and embedded in the Laboratory BASIS programming language framework. While BASIS is quite powerful and has a modest user base outside the Laboratory, it is used almost exclusively in codes developed at the Laboratory, has no internal or external developer base, and support has been discontinued. As a result of our research, the Python version can now be built in modern computers and works from the same source code as the latest mainstream BASIS UEDGE version. Test cases have been run with this and further research will result in translation of key application workflow scripts from BASIS to Python. This is a very important step towards usability, attractiveness to researchers, and longevity of UEDGE and its coupling to DEGAS-2. Python is widely used, extremely powerful, easy to build, and is a commonly used language in code integration frameworks for MFE simulation. While the mainstream BASIS UEDGE version is still viable and is the main production version, the move away from BASIS dependence is essential for the long-term viability of the UEDGE code and will also greatly improve couplings of UEDGE that can be done within MFE whole-device-modeling frameworks.
Impact on Mission
Understanding and predicting the transport of plasma, neutral species particles, and heat in the outer edge region of magnetic fusion plasmas is essential to success in magnetic fusion energy because these aspects strongly impact the overall plasma fusion performance; conditions there set temperature boundary conditions for the core temperature profile, determine the “fueling” (i.e., which and how much of any ionic species end up in the plasma core), and heavily impact the possible material damage that can result from high heat loads to material surfaces. Our research solved key problems in achieving this needed predictive capability and in so doing, directly contributed to the Laboratory's core competencies in high-energy-density science and computational science
This research addressed key issues on the DOE FESAC (2014) highest priority list of thrusts. It will strengthen Laboratory influence and collaboration with ITER and position the Laboratory to successfully compete in and provide scientific leadership for future DOE Office of Fusion Energy Sciences proposal calls.
This project also used and developed methods that are expected to result in improvements to computationally-intensive, kinetic-continuum coupling algorithms for other mission critical areas such as radiation and neutron transport.
Conclusion
This project made major advances in coupling computer models (or codes) in which there was a combination of numerical stiffness and MC noise. Our coupled UEDGE and DEGAS-2 MFE edge transport application code will be exercised for physics and design studies. Our work has also specifically drawn on and made contributions to numerical solutions of radiation and neutron transport.
We will fully document and publish our work on advanced algorithms in one or more articles in a relevant major technical journal. There is a possibility of continuing implementation of further components using the coupling algorithm through DOE programmatic funding.
This project has also put the coupled combination UEDGE and DEGAS-2 on a significantly improved footing with respect to usability and longevity. In particular, the Python version of UEDGE is much closer to becoming the mainstream version, including for coupled UEDGE and DEGAS-2 runs. These developments have greatly helped for the longevity and attractiveness of UEDGE to outside researchers.
References
Dekeyser, W. 2014. "Optimal Plasma Edge Configurations for Next-Step Fusion Reactors." Leuven: KU Leuven.
Fang, H. and Y. Saad. 2009. “Two classes of multisecant methods for nonlinear acceleration.” Numer. Linear Algebra Appl. 16: 197.
FESAC. 2014. "Fusion Energy Sciences Advisory Committee Report on Strategic Planning: Priorities Assessment and Budget Scenarios." Washington DC: U.S. Department of Energy Office of Science.
Kelley, C. T. 1995. "Iterative Methods for Linear and Nonlinear Equations." Philadelphia: Society for Industrial and Applied Mathematics.
———. 2013. “Newton’s method for Monte Carlo-based residuals.” Presentation at City University of New York, NY.
Kukushkin, A.S., et al. 2011. “Finalizing the ITER divertor design: The key role of SOLPS modeling.” Fusion Engineering and Design 86: 2865–2873.
ReNEW. 2009. "Research Needs for Magnetic Fusion Energy Sciences: Report of the Research Needs Workshop (ReNeW)." Bethesda, MD. June 8-12, 2009. DOE Office of Fusion Energy Sciences.
Rognlien, T.D., et al. 2002. “Edge-Plasma Models and Characteristics for Magnetic Fusion Energy Devices.” Fusion Engineering and Design. 60. 497.
Stotler, D. P. and C. F. F. Karney. 1994. “Neutral Gas Transport Modeling with DEGAS 2” Contrib. Plasma Phys. 34 (1994): 392-397.
Willert, J., et al. 2015. “Newton’s Method for Monte Carlo–Based Residuals.” Siam J. Numer. Anal. 53 (2015): 1738–1757.
Publications and Presentations
Dimits, A., et al. 2015. "Progress on Implicit Coupling of Fluid- Plasma and Monte-Carlo-Neutral Models for Edge Plasma Simulation." Presented at the Sherwood Fusion Theory Conference, New York, NY, March 17, 2015. LLNL-POST-668624.
———. 2016. "Efficient Implicit Coupling of Fluid-Plasma and Monte-Carlo-Neutral Models for Edge Plasma Transport," Presented at the Sherwood Fusion Theory Conference, Madison, WI, April 4, 2016. LLNL-POST-687428.
———. 2017. “Efficient Coupling of Fluid-Plasma and Monte-Carlo-Neutrals Models for Edge Plasma Transport.” Presented at the APS DPP Meeting, Milwaukee, WI, Oct. 25, 2017. LLNL-POST-740406.
Joseph, I., et al. 2015. "Efficient coupling of fluid plasma and kinetic neutral transport models.” Presented at the US-EU Transport Task Force Meeting April 29th, 2015. LLNL-POST-669959.
———. 2017 “On coupling fluid plasma and kinetic neutral physics models.” Nuclear Materials and Energy 12: 813-818.
Sjogreen, B. 2016. “Investigation of Iterative Methods for Solution of a Model Problem in Edge Plasma Simulation.” LLNL technical report. LLNL-JRNL-697766.