Modeling Materials Under Strongly Driven Conditions

Alfredo Correa Tedesco (14-ERD-103)

Abstract

Currently there are many instances, particularly for matter under extreme conditions, where basic accepted molecular dynamics approximations and assumptions are not appropriate. We advanced the field of quantum molecular simulations by developing a framework for nonadiabatic electron––nuclear dynamics (processes with energy transfer), which is a fundamental mechanism of state and phase changes in various dynamical processes of physics. Our objective for this project was to perform a series of landmark simulations for applications in the realm of radiation (light and matter effects), transport (linear and nonlinear conductivity), and high-energy molecular collision. At the same time, we maintained computational feasibility in the current technological context of massively parallel computation. With this project, we developed a new predictive simulation framework for nonadiabatic molecular dynamics by building upon our current implementation of coupled ion and electron dynamics (Ehrenfest nonadiabatic interactions between electrons and ions), where the time-dependent dynamics of electrons is taken into account explicitly.

Background and Research Objectives

The Born–Oppenheimer approximation¹ (separation of atomic nuclei and electron motion) and the assumption of thermal equilibrium between ionic and electronic subsystems, are ubiquitous in the field of molecular dynamics. However, there are many instances, particularly for matter under extremely driven conditions, where these basic approximations are not appropriate. We developed a platform to perform a new type of predictive simulation for nonadiabatic molecular dynamics by building upon our implementation of Ehrenfest coupled electron–ion dynamics, where the time-dependent dynamics of electrons and ion back reaction is taken into account explicitly.²

Most theories and simulation tools that perform molecular dynamics integrate out the electronic degrees of freedom, which only enter implicitly into the model of interatomic forces, to represent atomic motion and predict properties and response of matter. Ab initio (quantum) molecular dynamics takes account of electronic degrees of freedom, but assumes that electrons are in a well-defined thermal state (usually the ground state). At best, electrons do not have any independent dynamics. This assumption is known as the adiabatic or Born–Oppenheimer approximation and is well justified in many applications. However, when matter is driven out of equilibrium, the approximation breaks down and the methods used need to be changed in a nontrivial way.

Because of their intrinsic timescale, strong pulsed-light (lasers) and high-energy radiation sources mainly affect electrons, which are lighter (easier to accelerate) and have faster characteristic velocities (Fermi or atomic velocity) than the nuclei. After such initial excitation, the dynamics of the electron becomes separate from that of the nucleus, in what is known as nonadiabatic or beyond-Born–Oppenheimer dynamics. It is only recently that the computational resources,³ theory,⁴ and algorithm development² allowed for the explicit time dynamics of interacting quantum electrons. Moreover, this method, although an approximation to the time-dependent many-body Schrödinger equation, is still parameter-free.

The objective of this project was to advance the field of quantum molecular dynamics to include nonadiabatic effects, perform a series of landmark simulations for applications in the realm of radiation (light and matter effects), transport (linear and nonlinear conductivity), and high-energy molecular collision, and at the same time, maintain computational feasibility in the current technological context of massively parallel computation.

Scientific Approach and Accomplishments

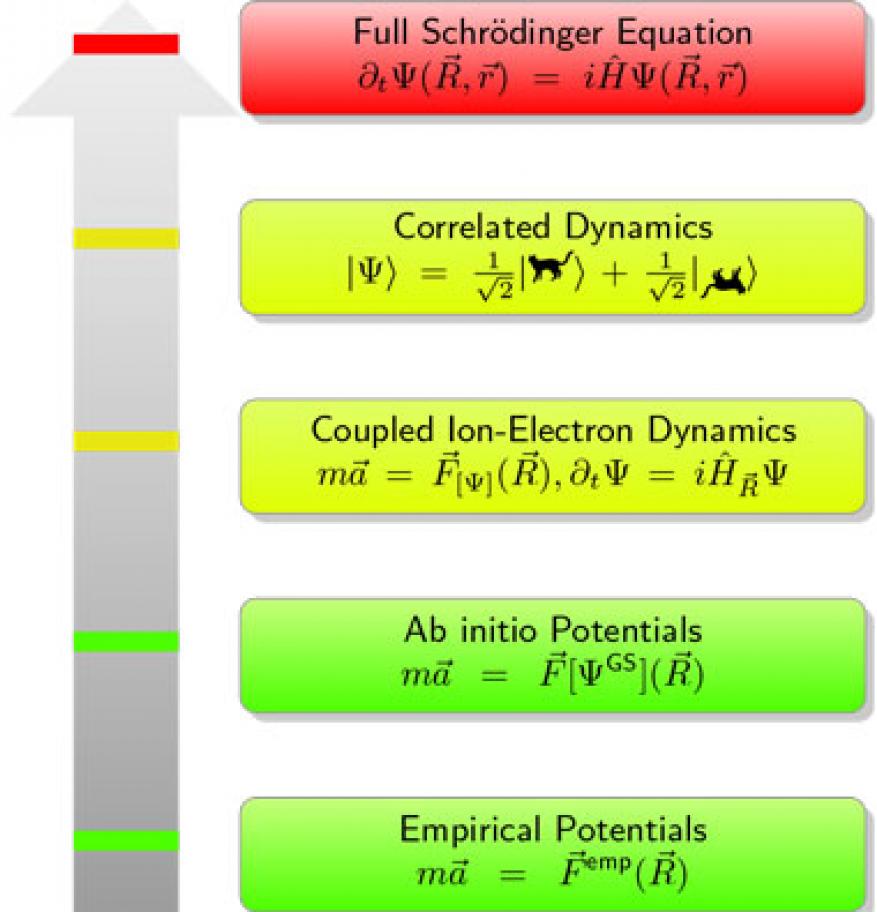
The basis of the scientific approach is the application of the generally accepted microscopic theory in which electrons and elemental nuclei of various atomic numbers are the fundamental particles, in combination with well-known approximations for particle interactions that make the problem manageable (Figure 1). The resulting mathematical equations (initial value, nonlinear partial-differential equations) are integrated numerically in a parallel computer through efficient algorithms. Simulations of various systems are performed, and both the approximations and the numerical implementation are tested and validated against existing experimental results. Further simulations are interpreted as predictions of the theory within its range of validity.

The fundamental equations to be solved (propagated in time) consist in a time-dependent Schrödinger-like equation of the quantum motion for each individual electron. The electron–electron interaction is approximated by a mean field theory formally derived from density functional theory.⁵ Electrons interact through the self-consistent potential generated by the electronic density (a Coulomb electrostatic contribution plus a term that captures the exchange and correlation energy taken, for example, from Perdew and Zunger.⁶) The resulting equations are known as the time-dependent Kohn–Sham equations for the time-dependent density functional theory. There is a set of corresponding Newtonian equations of motion for the nuclei coordinates.

In our numerical implementation of the time evolution of this equation, the most challenging part is the numerical representation of the solution. The choice of periodic boundary conditions makes the method applicable to bulk materials, as well as to an isolated system if surrounded by enough vacuum. It also makes it convenient to use a plane-wave basis or Fourier representation. This gives a basis representation for periodic smooth functions. To keep the number of coefficients small, we need to devise a numerical approximation of the singular (Coulomb) electron–ion interaction term, and replace it by a nonlocal but smooth operator that has the same scattering properties as the singular potential and also includes the effect of core electrons (non-valence electrons). Core electrons are inefficient to simulate and except for very-high-energy applications such as hard x rays, they don't participate actively. This is known as the pseudopotential approximation.

Implementing from scratch the code to handle the pseudopotential approximation is a formidable task. Fortunately, our implementation of time-dependent electronic dynamics leverages an existing well-debugged code, Qbox,⁷ developed at Livermore. Qbox is a C++ message passing interface open-source implementation of the plane-wave method for adiabatic quantum molecular dynamics. Our modifications to handle explicit time-dependency have been ported to the Qb@ll code, a derivative of Qbox tuned for the last generation of parallel computers. In the following sections, we describe both technical and application accomplishments.

Enforced Time-Reversal Symmetry Propagator

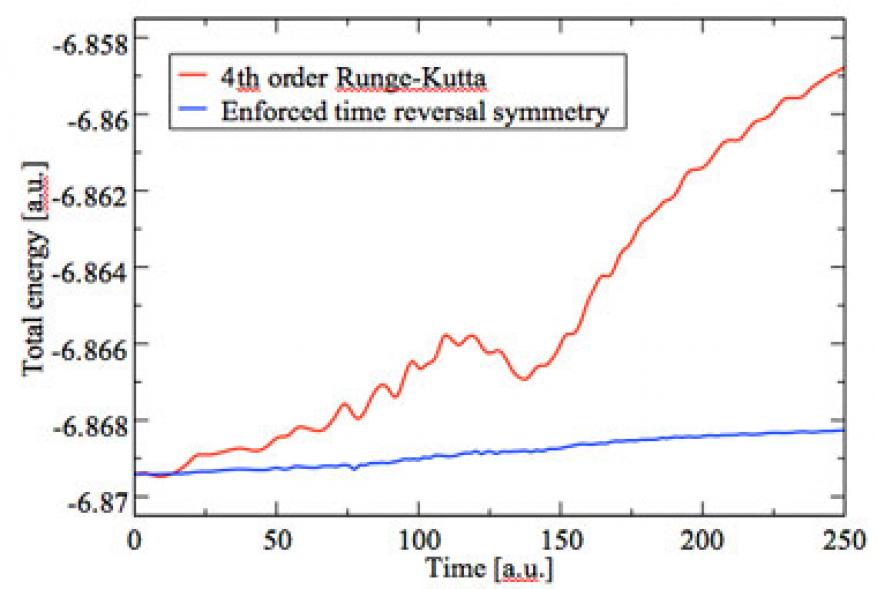
Our implementation is based on the Qbox code, over which we developed a series of time integrators (absent in the original version). Our early study of integrators was published by Schleife in 2012.² It is worth mentioning that we discovered that fourth order Runge–Kutta showed a particular balance of robustness and efficiency. Runge–Kutta is a generic and simple integration scheme that we used in several applications.^8,9 Precise optimization of discrete time step Δt is system-dependent. Typically, the method allowed us to use Δt ≃ 1 as (10⁻¹⁸ s).

Fourth order Runge–Kutta has no particular property regarding exact conservation of energy (energy and norm is only conserved up to the order of integration). Because energy is a conserved quantity in closed systems, some potential applications call for integrators, which, although approximate in many respects, conserve energy exactly or do it to a much higher order. For this reason, we decided to investigate other integrators.

We have implemented a method known as the enforced time-reversal symmetry propagator¹⁰ in the Qbox and Qb@ll codes. Because this method is explicitly time-reversible, it has better energy and charge (orthonormality) conservation properties than the Runge–Kutta method that we have implemented previously with a similar computational cost. The energy conservation property is illustrated in Figure 2. Enforced time-reversal symmetry allowed us to double the time step when compared to fourth order Runge–Kutta. We have also made improvements to the original algorithm. Enforced time-reversal symmetry requires the evaluation of three exponential operations. We have found a way of merging two of these evaluations into a single evaluation, reducing the overall cost of the propagation by one third.

Computer Parallelization

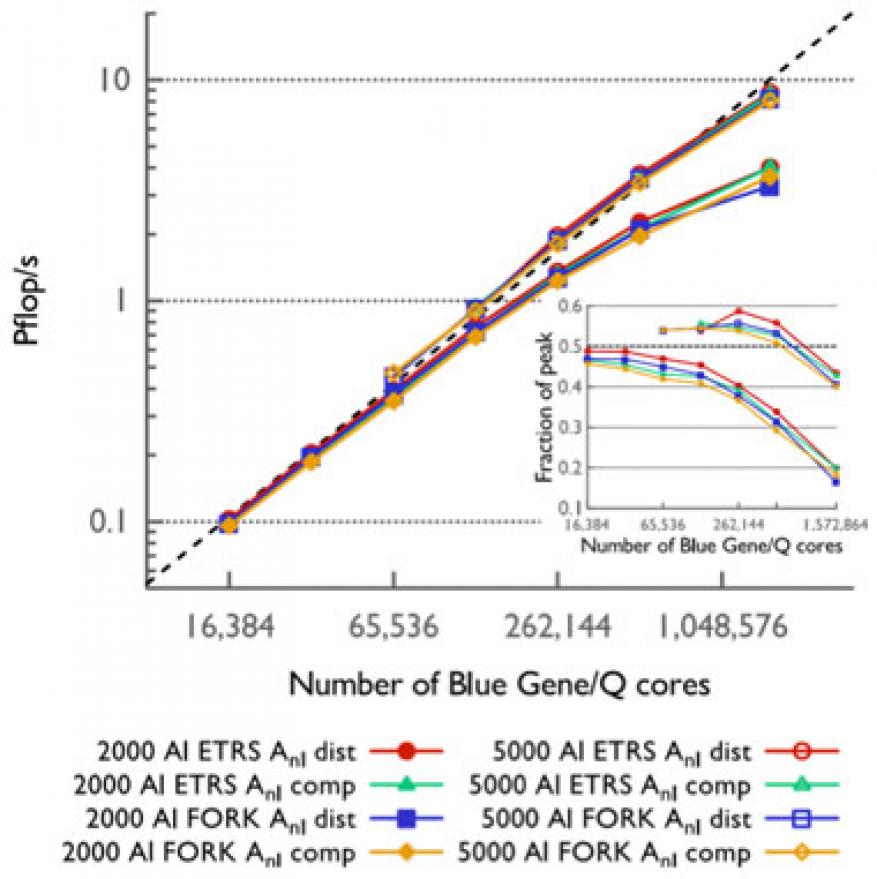
An important goal of our project was to retain or outperform parallelization of the original Qbox code. Our code results in a highly scalable parallel implementation of first-principles electron dynamics coupled with molecular dynamics. By using optimized kernels and network-topology-aware communication, and by fully distributing all terms in the time-dependent Kohn–Sham equation, we demonstrated unprecedented time-to-solution for disordered aluminum systems of 2,000 atoms (22,000 electrons) and 5,400 atoms (59,400 electrons), with wall clock time as low as 7.5 s per molecular dynamics time step (Figure 3).

The Kohn–Sham formalism requires the set of orbitals to be orthogonal to each other. In adiabatic methods such as Born–Oppenheimer or Car–Parrinello,¹¹ orthogonality of the orbitals is not preserved and has to be imposed at each iteration through an expensive N³ procedure (N is the number of electrons) that mixes different orbitals. In the context of parallel computing, this requires large-scale linear algebra operations that involve all nodes. Electron dynamics, by contrast, preserves the orthogonality of the set during propagation as long as the numerical method is sound. By choosing an adequate propagator (see above), this property is retained automatically by the numerical implementation. The absence of an orthogonalization step makes the overall computational cost lower, but more importantly, less inter-processor communication is required, because most operations involve communication along the columns or rows of the process grid.

Despite a significant amount of nonlocal communication required in every iteration, we achieved excellent strong scaling and sustained performance on the Sequoia BlueGene/Q supercomputer at Lawrence Livermore. We obtained up to 59% of the theoretical sustained peak performance on 16,384 nodes and performance of 8.75 petaflop/s (43% of theoretical peak) on the full 98,304-node machine (1,572,864 cores). No other electronic code (adiabatic or nonadiabatic) runs at this level of performance (8 petaflop/s). Our article on the simulation won the best paper award at the 2016 IEEE International Parallel and Distributed Processing Symposium.¹² Our project was consistently awarded tier-1 computer allocations, 6,000,000 core-hours/week, from LLNL's Institute for Scientific Computing Research.

Conductivity

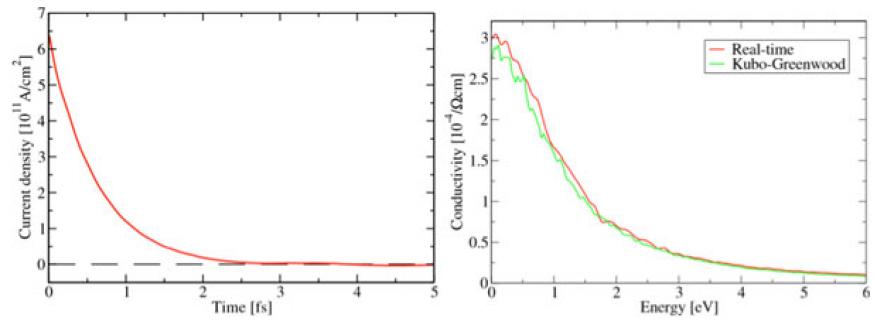
We have developed a method to calculate conductivity of metals based on electron dynamics. The method predicts the conductivity of metals without the need of any empirical parameters such as relaxation times or mean-free paths. To obtain the conductivity, we induce a current on the system and simulate its evolution using the real-time, time-dependent density functional theory equations. Because of the scattering of ions, this initial electronic current will dissipate. From how the current decays, we can obtain the frequency-dependent conductivity of the system using a Fourier transform.

In Figure 4, we show our results for the calculation of the conductivity of liquid aluminum. We first induce a current in the system of approximately 6 × 10¹¹ A/cm, which decays to 0 in around 3 or 4 fs. From this function, we calculate the frequency-dependent conductivity, which we compare with the one obtained from the same system using the Kubo–Greenwood approach. Kubo–Greenwood is the method commonly used to obtain conductivity from atomistic simulations. We can see that both methods agree quite well for this system in the studied regime.

A unique property of our new method is that we can directly get the zero-frequency (or direct-current) conductivity, which is often the experimentally accessible quantity. By providing direct access to the direct-current conductivity, we avoid the extrapolation to zero frequency that is required for Kubo–Greenwood calculations and that introduces additional approximations.

Our method has additional advantages over Kubo–Greenwood. It is more accurate, because it includes the full response in time-dependent density functional theory (including nonlinear effects). It does not require unoccupied states, making the calculation simpler to set up and more accurate, and it scales as N², while Kubo–Greenwood has N³ scaling. We have implemented the method in the open-source code OCTOPUS, used in time-dependent density functional theory calculations, and Qbox.

Electronic Stopping Power

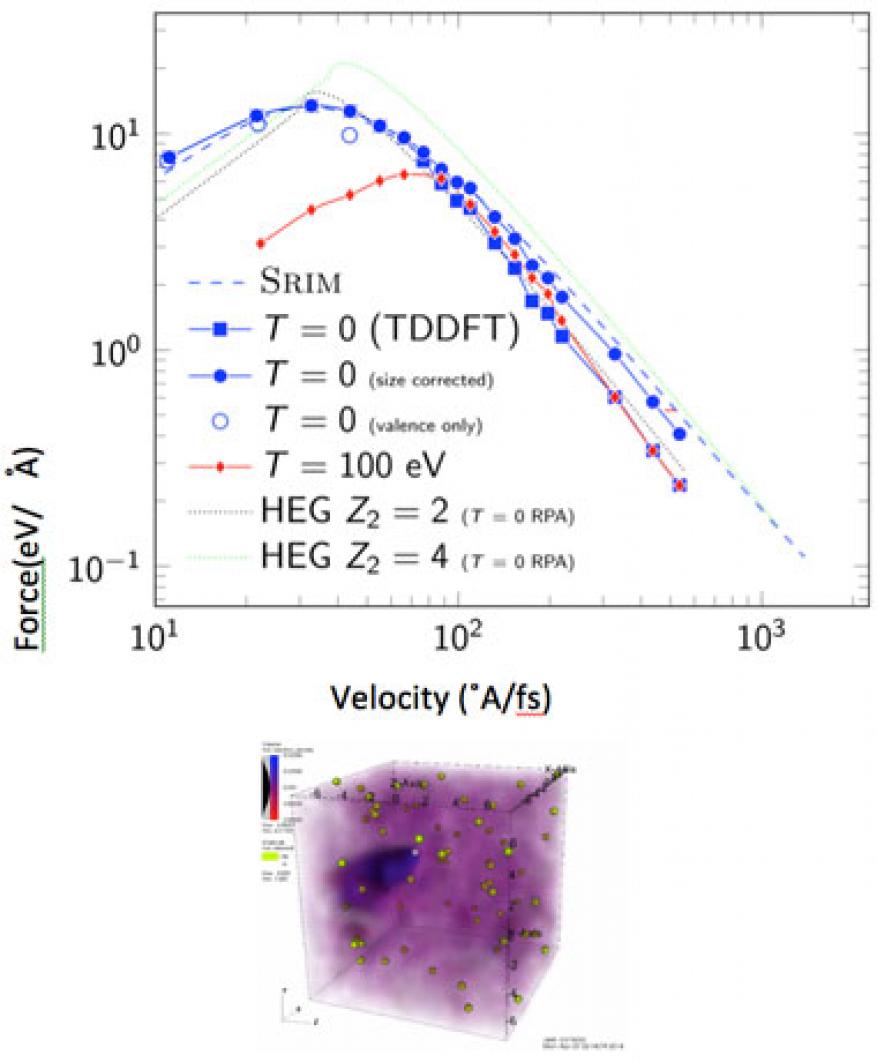
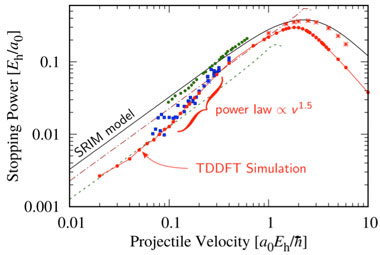
Electronic stopping power is the quintessential non-adiabatic effect, in which electrons absorb energy irreversibly from a fast-moving ion—for example resulting from particle radiation. We performed simulations of electronic stopping power of low-atomic-number ions (hydrogen, helium, lithium, and silicon) in aluminum, gold, silicon, and beryllium (Figure 5). In the case of metallic systems, we discovered that to get accurate results of electronic stopping, weighted channeling and off-channeling trajectories for the ions and semi-core electrons need to be taken into account.^8,9

In the case of semiconductors (or materials with electronic gaps), it was shown that a lower-velocity threshold for electronic stopping is absent. Instead, an intricate structure (as a function of velocity) was evidenced from simulations. This is an important effect that will lead to improving force-field large-scale molecular dynamic simulations. This simulation capability is used to predict defect formation after ionization cascades.^13,14 Another important application was to use the case of copper to show the influence of band structure effects (Figure 6).¹⁵

Additionally, we extended the method to the plasma regime in which the initial temperature of electrons is chosen to an arbitrary value. We performed the first calculation of electronic stopping of hot dense beryllium. We have also shown that the electron–phonon coupling can be regarded as a low-energy electronic stopping power for vibrating classical ions.¹⁶ These discoveries required large supercells (in excess of 200 atoms and 1,000 electrons) to demonstrate the effect, something that can only be achieved with the current computing scalability provided by this project.

Molecular Collisions

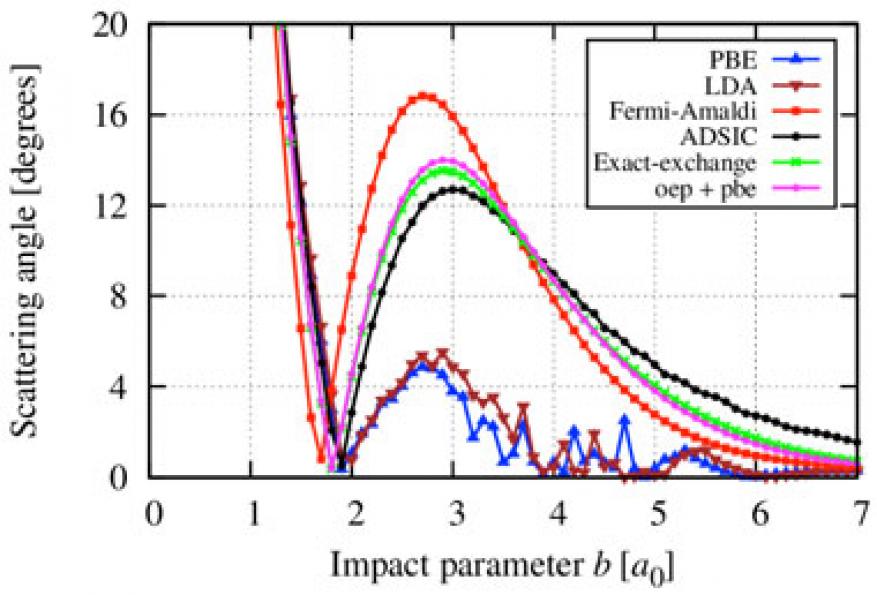
Finally, we applied our method to the problem of molecular collisions. The fields of atomic collision and quantum chemistry have historically been developed using different techniques. Our approach allows the unification of these two fields. The idea is that each molecule can be well described by the accuracy that is characteristic of the time-independent method (density functional theory) and, at the same time, electronic excitations resulting from the collision of these molecules can be described well with the time-dependent aspect of our method. A prototypical case is the collision between a proton and a methane molecule. We performed scattering simulations in which the proton is set into direct collision with the molecule initially in the ground state based on various computational schemes (Figure 7).

We discovered that scattering results are very sensitive to the level of theory using the density functional theory approximation, in particular depending on how the self-interaction corrections are managed. Theories with no self-interaction corrections give very low (and noisy) scattering angles.

Impact on Mission

Our research into electromagnetic coupling, swift ions, and two-temperature systems has direct relevance to both NNSA and LLNL missions in national and energy security. The Laboratory's core competency in advanced materials and manufacturing will also benefit from our modeling of materials under strongly driven conditions (high-energy-density science). In addition, our code can make efficient use of existing high-performance computing platforms at LLNL, and will be available for Laboratory researchers for various programmatic applications.

Conclusion

The simulation of electron dynamics is now possible for large-scale applications, and bulk and isolated systems with hundreds of atoms and thousand of electrons can be simulated routinely. This is a unique capability, both in terms of simulation capability and hardware utilization. We have applied our simulation capability to problems that were previously outside of the realm of quantum or molecular dynamics simulations, including transport and electronic stopping power. In addition, we have demonstrated record performance on the Laboratory's Sequoia BlueGene/Q supercomputer, one of the largest computers in the world. As part of this project, we have hired a new postdoctoral researcher, and developed several collaborations involving postdoctoral researchers at Imperial College in the United Kingdom; University of California, Berkeley; and Florida A&M University. Some of our project's capabilities are now being applied to alloy material research in the Energy Dissipation to Defect Evolution Center, which is part of the DOE Office of Science's Energy Frontier Research Center.¹⁷

References

1. Born, M., and R. Oppenheimer, “Zur quantentheorie der molekeln.” Ann. Phys. 389(20), 457 (1927).
2. Schleife, A., et al., Plane-wave pseudopotential implementation of explicit integrators for time-dependent Kohn–Sham equations in large-scale simulations. J. Chem. Phys. 137(22), 22A546 (2012).
3. Wikipedia, IBM Sequoia. (2015). https://en.wikipedia.org/wiki/IBM_Sequoia
4. Runge, E., and E. K. U. Gross, “Density-functional theory for time-dependent systems.” Phys. Rev. Lett. 52, 997 (1984).
5. Kohn, W., and L. J. Sham, “Self-consistent equations including exchange and correlation effects.” Phys. Rev. 140, A1133 (1965).
6. Perdew, J. P., and A. Zunger, “Self-interaction correction to density-functional approximations for many-electron systems.” Phys. Rev. B 23, 5048 (1981).
7. Gygi, F., et al., “Gordon Bell finalists I—Large-scale electronic structure calculations of high-z metals on the BlueGene/L platform.” Proc. 2006 ACM/IEEE Conf. Supercomputing—SC '06. ACM Press, New York, NY (2006).
8. Schleife, A., et al., “Quantum dynamics simulation of electrons in materials on high-performance computers.” Comput. Sci. Eng. 16(5), 54 (2014).
9. Schleife, A., Y. Kanai, and A. A. Correa, “Accurate atomistic first principles calculations of electronic stopping.” Phys. Rev. B 91, 014306 (2015).
10. Castro, A., M. A. L. Marques, and A. Rubio, “Propagators for the time-dependent Kohn–Sham equations.” J. Chem. Phys. 121(8), 3425 (2004).
11. Car, R., and M. Parrinello, “Unified approach for molecular dynamics and density-functional theory.” Phys. Rev. Lett. 55, 2471 (1985).
12. Draeger, E. W., et al., Massively parallel first-principles simulation of electron dynamics in materials. 2016 IEEE Intl. Parallel and Distributed Processing Symp. (IPDPS), Chicago, IL, May 23–27, 2016.
13. Horsfield, A. P., et al., “Adiabatic perturbation theory of electronic stopping in insulators.” Phys. Rev. B 93, 245106 (2016).
14. Lim, A., et al., “Electron elevator: Excitations across the band gap via a dynamical gap state.” Phys. Rev. Lett. 116, 043201 (2016).
15. Quashie, E. E., B. C. Saha, and A. A. Correa, “Electronic band structure effects in the stopping of protons in copper.” Phys. Rev. B 94, 155403 (2016).
16. Caro, A., et al., “Adequacy of damped dynamics to represent the electron-phonon interaction in solids.” Phys. Rev. B 92, 144309 (2015).
17. Zhang, Y., Energy dissipation to defect evolution. Oak Ridge National Laboratory, Oak Ridge, TN. (2015).

Publications and Presentations

• Caro, A., et al., “Adequacy of damped dynamics to represent the electron-phonon interaction in solids.” Phys. Rev. B. 92, 144309 (2015). http://dx.doi.org/10.1103/PhysRevB.92.144309
• Horsfield, A. P., et al., "Adiabatic perturbation theory of electronic stopping in insulators." Phys. Rev. B 93, 245106 (2016). LLNL-JRNL-727616. https://doi.org/10.1103/PhysRevB.93.245106
• Schleife, A., Y. Kanai, and A. C. Correa, “Accurate atomistic first-principles calculations of electronic stopping.” Phys. Rev. B. 91, 014306 (2015). http://dx.doi.org/10.1103/PhysRevB.91.014306
• Schleife, A., et al., "Quantum dynamics simulation of electrons in materials on high-performance computers." Comput. Sci. Eng. 16(5), 54 (2014).
• Tedesco, A. C., “Accurate atomistic first-principles calculations of electronic stopping.” Phys. Rev. B. 91 (2015). LLNL-JRNL-666354. http://dx.doi.org/10.1103/PhysRevB.91.014306
• Tedesco, A. C., “Electronic band structure effects in the stopping of protons in copper.” Phys. Rev. B. 94 (2016). LLNL-JRNL-680464. http://dx.doi.org/10.1103/PhysRevB.94.155403