Carol Woodward (17-ERD-035)
Executive Summary
We are developing time-integration software that accommodates widely varying timescales commonly found in multiphysics simulations (such as atmospheric climate modeling), where cloud microphysics, fluid dynamics, and ocean currents each evolve at different rates. This research supports national missions that rely on complex simulations, such as energy and nuclear security.
Project Description
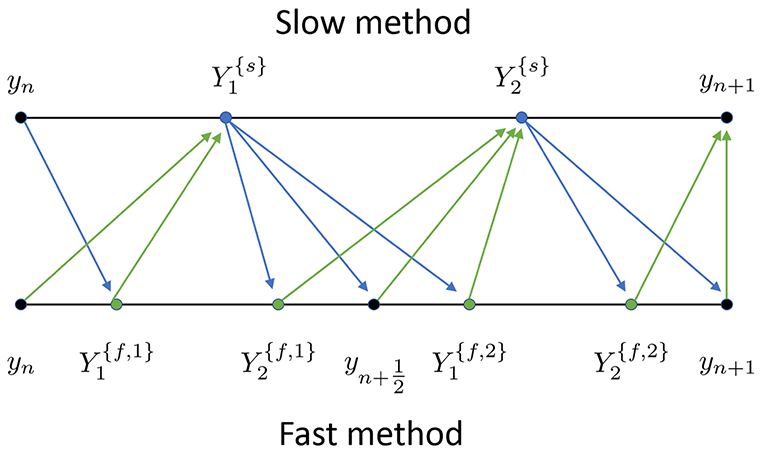
The advent of exascale computing systems will enable simulations to create far larger and more complex models than ever before. As a result, scientific simulations (such as in climate, combustion, power-grid, and hydrological sciences) will include more physics, resulting in a growing number of changing timescales. Widely varying timescales are common in multiphysics problems, such as atmospheric climate modeling, where cloud microphysics, fluid dynamics, and ocean currents each evolve at different rates. Timescales can also differ significantly within a single physics discipline. For example, in combustion, timescales can span femtoseconds to seconds. Currently, methods are lacking for these multiple-rate problems. By focusing work where it is needed the most, multirate time integrators have shown three-fold to tenfold increases in speed on model problems in the literature. To meet the needs of increasingly multiscale simulations arising from opportunities of exascale computing, we are developing multirate numerical time integrators targeted at problems of interest to the DOE. These methods will be developed as prototypes with an eye toward future inclusion into the SUNDIALS software library of time integrators for differential equations. We will establish a stability-and-accuracy theory for candidate schemes and develop effective timescale-partitioning methods in tandem with parallelization strategies. Our prototype implementations will aid in later development of a general-purpose software package. Finally, we will test our multirate integrators in combustion and multiphysics climate simulations.
Serial implementations of multirate time integrators have shown significant speedups over single-rate integrators on a variety of benchmark cases. We expect to extend efficiency benefits of such methods to parallel multi-timescale applications, such as combustion, that suffer from a single-rate integrator, slowing solution of an entire problem to ensure accuracy of a small number of variables. Specific objectives include focusing on identification and development of explicit, implicit, and mixed explicit and implicit multirate integrators for both problems with multiple processes (each with its own timescale) operating on a common set of unknowns (additive processes), and problems with unknowns that evolve at differing timescales (variable partitioned processes). The work will build upon established methods to complete stability analysis and derive methods where needed. In addition, we will develop time-step selection and parallel partitioning methods. The work will leverage weak coupling in the system through error estimation, dependence graph analysis, and sensitivity monitoring. Our work will result in prototype codes that will inform software design needs in a common infrastructure for implementations of diverse multirate integrators. Our methods will also bring robustness to multiphysics applications, such as climate, which currently use more ad hoc methods. Implementation of prototype software will make multirate methods accessible to large-scale problems, for which there is currently only limited adoption, and set up future inclusion of multirate schemes into the SUNDIALS integrator suite.
Mission Relevance
This research supports the NNSA goal of advancing the scientific, technological, and engineering competencies. Specifically, we are enhancing the Lawrence Livermore National Laboratory’s core competency in high-performance computing, simulation, and data science by elucidating temporal discretization and multiple-scale and multiphysics methods, including methods to increase fidelity while focusing on accurate coupling between scale. Additionally, our effort in multi-rate time integrators will result in a suite of methods adaptable to efficient implementation on exascale computer systems and ensure robust coupling between timescales. Our work will also support the Laboratory's energy and climate security strategic focus area by providing more-efficient time integration in simulations of combustion and atmospheric climate.
FY17 Accomplishments and Results
In FY17, we (1) evaluated papers on generalized additive Runge-Kutta methods and multirate variants, waveform relaxation methods, signal-flow variable partitioning, and multirate variational integrators, schemes, and stability analysis; (2) implemented several methods (up to third-order) and test problems for variable partitioned problems using both C and Matlab; (3) conducted initial stability tests with these codes; (4) placed all codes in an institutional git repository (a version control system); and (5) began developing application-specific test problems with combustion and climate teams.