1. Home
  2. Report Archives
  3. FY2015 LDRD Annual Report
  4. Advanced Materials and Manufacturing - 2015
  5. Accelerated Certification for Additively Manufactured Metals

Accelerated Certification for Additively Manufactured Metals

Wayne King (13-SI-002)

Abstract

The metal laser powder-bed fusion additive-manufacturing process uses high-power lasers to build parts layer upon layer by melting fine metal powders. Qualification of parts produced using this technology is broadly recognized as a significant challenge. Physics-based process models have been identified as being foundational to qualification of additively manufactured metal parts. We developed a multiscale modeling strategy that will serve as the foundation upon which process control and part qualification can be built. This strategy includes a model at the scale of the powder that simulates single-track and single multiple-layer builds, and provides powder-bed and melt-pool thermal data. This model has provided insights as to the dynamics of melt pool and powder interaction and demonstrated formation of ejecta resembling the high-speed video results. A second model computationally builds a complete part and predicts manufactured properties (residual stress and dimensional accuracy) in three dimensions. That model has shown promising results in comparisons of residual stresses measured via neutron diffraction and digital image correlation techniques. Modeling is tied to experiment through data mining and uncertainty analysis. Such data analyses have demonstrated the ability to help guide rapid identification of baseline process parameters when initiating fabrication with a new material system. Experimental efforts included the measurement of laser absorption of powder samples for a variety of materials.

Background and Research Objectives

Stockpile stewardship requires a new manufacturing approach that can speed development and certification of parts, reduce the manufacturing footprint for a shrinking stockpile, reduce manufacturing waste, avoid the costs and delays normally associated with manufacturing processes, and reduce energy consumption in part fabrication. In this project, we employed modeling, simulation, process optimization, experiment design, in situ sensing, and uncertainty quantification for the accelerated certification of metals produced by additive manufacturing, with the goal of guiding the process to yield optimized properties and performance. We employed an effective medium simulation that models the process at the scale of the part and a powder simulation that models the process at the scale of the material powders used in parts manufacturing. Our accelerated certification of additively manufactured metals project advanced the field of additive manufacturing by (1) providing a multiscale modeling and inverse-design methodology to assist in navigating complex process–structure–property relationships, (2) developing a thorough understanding of the basic physics of additive-manufacturing processes to capture the complexity in the multiple interacting physical phenomena, (3) developing sufficient understanding of processes to be able to prescribe processing conditions and achieve the desired properties in one or two attempts, and (4) providing a strategy to accelerate the qualification of critical materials and parts.1

Scientific Approach and Accomplishments

Fundamental Aspects of Melting

An important component of metal additive-manufacturing process modeling efforts is the description of absorption of laser light by metal powder and the spatial distribution of absorbed energy. Direct measurements of absorption are quite difficult. And, it is problematic to use measurements without detailed specification of the powder, including the material, size distribution, spatial distribution of particles, and laser-beam size and profile. Thus, it is not sufficient to know only the results for one particular powder of a given material and for a particular laser. Similarly, the spatial distribution of absorbed energy is difficult to obtain experimentally.

Boley et al. discussed two different types of powders: Gaussian and bimodal distributions.2 The bimodal powder was chosen because of its high density (or low porosity). For a moderately absorbing metal such as stainless steel, the difference in absorptivity between Gaussian and bimodal powders is a few percent. Thus, the absorption capabilities of stainless steel and titanium are not very sensitive to powder layer structure. On the other hand, for highly reflective metals such as silver and gold, the variation in absorption can be nearly a factor of two. In these cases, multiple scattering is very important.

Measurements were carried out for 316L stainless steel, the Grade 5 titanium alloy Ti–6Al–4V (titanium alloyed with 6% aluminum and 4% vanadium), and 99.9% purity aluminum powder.3 The absorptivity value for the titanium alloy in our measurements is about 70%, somewhat higher than predicted by the modeling value of approximately 65%. Calculated values for aluminum are very different from the measurements. They suggest that the oxide layer and the structure of the surface are important. For a flat surface, the observed absorptivity of aluminum is over 20%, much higher than the 5% value predicted using the textbook refractive index. 4 The increase in powder absorptivity in comparison with a solid material is consistent with numerical results.2

Powder Model

The powder model uses the input laser-beam characteristics to transform a particle bed through the dynamics of the molten state into solidified material. The model is initialized with powder particles of desired size distribution and layer thickness. The combined thermal and hydrodynamic simulations model the appropriate distribution of the laser’s energy as it interacts with the powder particles, the substrate, and the melt pool. The deposited energy from the laser heats the powder well above the melting point, where the model coalesces the particles into a melt pool that flows under the influence of surface tension and vaporization recoil. The powder model tracks the various modes of heat loss, including conduction and evaporation, until the melted material solidifies.5

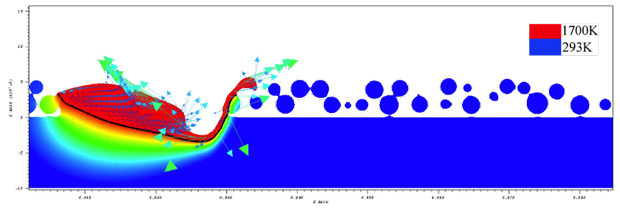
Figure 1 illustrates the melt pool dynamics in a slice taken through the center of the laser path, with color indicating temperature and vectors representing the velocity field. Hot droplets are ejected from the melt pool, like the sparking that is observed experimentally. Spatter of liquid droplets is observed in front of the laser spot. Recoil pressure has a significant effect on the topology of the powder and melt, allowing melt penetration well into the solid substrate. Marangoni convection is moving the surface of the melt away from the laser, but the curvature of the melt surface is strongly pulling the melt back into the depression formed by the laser beam.

Figure 1. this two-dimensional longitudinal simulated slice is taken in the middle of the melt track of a powder model of additive manufacturing of metal with a laser and powder particles. colors indicate the temperature distribution in the melt pool and substrate, with red being melted material, while the vectors represent melt velocities. the “floating” powder particles result from the two-dimensional slice through a random three-dimensional distribution. the domain pictured is approximately 850 µm in len
Figure 1. This two-dimensional longitudinal simulated slice is taken in the middle of the melt track of a powder model of additive manufacturing of metal with a laser and powder particles. Colors indicate the temperature distribution in the melt pool and substrate, with red being melted material, while the vectors represent melt velocities. The “floating” powder particles result from the two-dimensional slice through a random three-dimensional distribution. The domain pictured is approximately 850 µm in length.
 
Effective Medium Model

With an effective medium model such as discussed here, the geometry of powder particles is not resolved. We have analyzed representative volume-element domains consisting of a cubic millimeter of material.6 In this case, successive 50-µm layers of powder are initialized and scanned by moving the energy source location. To model the gross loss of porosity from powder melting, we introduced an irreversible "phase strain" into the thermo-mechanical constitutive model that is activated during the material’s first excursion above Tsolidus. This "phase strain" magnitude was simply assigned to result in a net volume associated with full-density material.

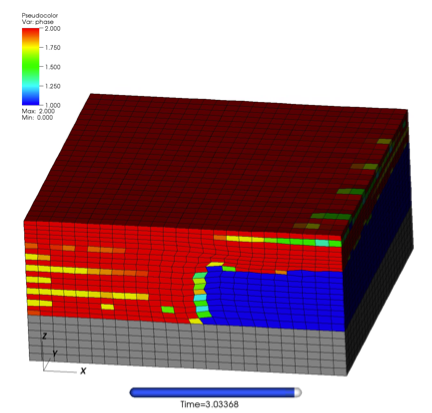
We considered a case where examining the limited domain of a representative volume provides insight into a common selective-laser-melting challenge: fabrication of downward-facing surfaces. Such "overhang" features often result in an undesirable finish on the underside that could necessitate further machining—if accessible. Figures 2 and 3 contrast two build strategies. A common domain is defined: a 1-mm2, plan form starting on a build plate is shown in grey. For the first six layers, the energy source only scans over the left half. Blue represents unconsolidated powder and red the fully transformed material. Intermediate colors represent incompletely consolidated material. Starting with the seventh layer, the energy source scans the entire plan form. With the strategy shown in Figure 2, which maintains constant laser power, we see the relative insulating properties of powder lead to localization of the energy and deeper penetration of the melt pool. In Figure 3, the laser power is modulated to one-fourth its nominal value as it reaches the right edge of the domain. This produces a transformed overhang region much nearer the desired horizontal surface. Note, however, this simulation also shows the mitigation strategy should only be utilized during the initial overhang layers. By the third overhang layer, the reduced power is leading to substantially incomplete melting of the powder as evidenced by the green regions.

Sfigure 2. in this overhang fabrication scenario, constant laser power is maintained throughout the build scans. the domains are 1 mm<sup>2</sup> in plan form. the grey base represents the build plate, blue untransformed powder, and red fully transformed material.
Figure 2. In this overhang fabrication scenario, constant laser power is maintained throughout the build scans. The domains are 1 mm2 in plan form. The grey base represents the build plate, blue untransformed powder, and red fully transformed material.

 

Figure 3. in this overhang fabrication scenario, the laser power is modulated whenever the scans extend into the overhang section, leading to a more uniform build thickness. the domains are 1 mm<sup>2</sup> in plan form. the grey base represents the build plate, blue untransformed powder, and red fully transformed material.
Figure 3. In this overhang fabrication scenario, the laser power is modulated whenever the scans extend into the overhang section, leading to a more uniform build thickness. The domains are 1 mm2 in plan form. The grey base represents the build plate, blue untransformed powder, and red fully transformed material.
Data Mining and Uncertainty Analysis

The Eagar–Tsai model,7 combined with sampling techniques, feature selection, and the building of data-driven predictive models, enables us to determine the melt-pool characteristics for a given power and speed combination. The accuracy of these predictions depends on the number and location of the sample points, the accuracy of the physics model, as well as the complexity of the function being predicted. We used the Eagar–Tsai model to determine the viable region of power and speed (these being the most important variables) and then selected a few points in this region for single-track experiments. Once we knew the actual melt-pool characteristics at specific power and speed values, we used them to identify process parameters for building small, three-dimensional pillars for density studies.

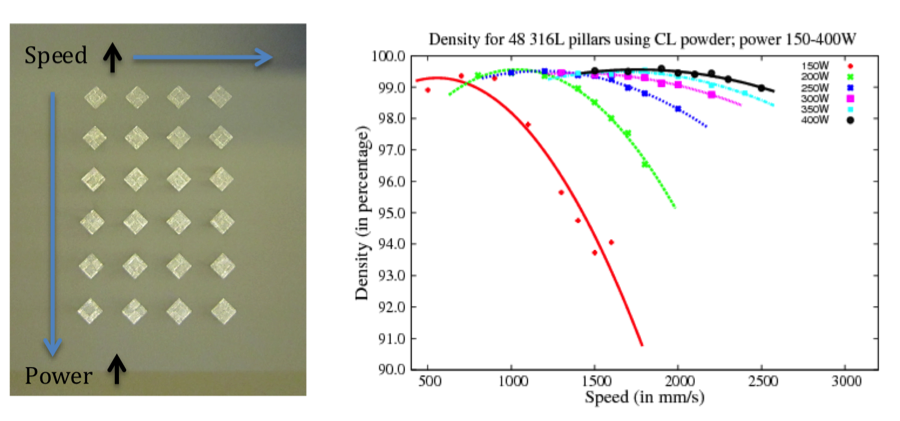
Figure 4 shows the first set of 24 pillars of 316L stainless steel, along with the density for the first two sets of pillars. Each pillar is 10 x 10 x 8 mm. Having obtained the density data for the first set of 24 pillars, we ran another 24 at the same power values, but with the speeds chosen to complete the gaps in the density curves.8

Figure 4. our first set of 24 steel pillars constructed for density studies (left). manufacturing speed increases from left to right and power increases from top to bottom. on the right, the density of pillars from the first two sets, built using 316l powder.
Figure 4. Our first set of 24 steel pillars constructed for density studies (left). Manufacturing speed increases from left to right and power increases from top to bottom. On the right, the density of pillars from the first two sets, built using 316L powder.
 

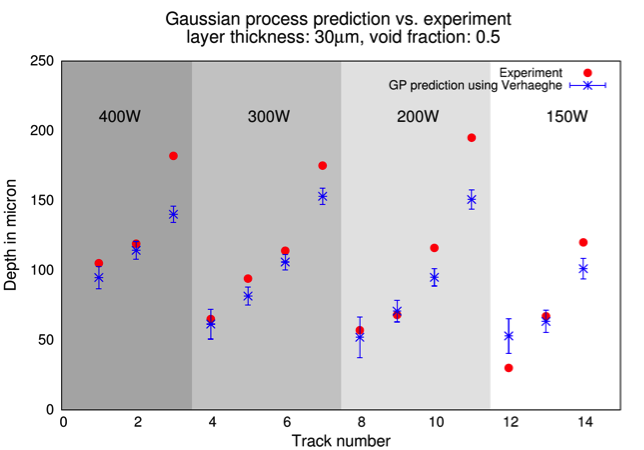
We next ran the more-complex Verhaeghe model, which includes a powder layer, at the 41 sample points in the viable space of the Eagar–Tsai parameters.9 The resulting more-accurate values of the melt-pool depth were then used to build a Gaussian process model, which predicts not only the depth, but also the associated uncertainty, at any point in the viable space. Figure 5 shows that the Gaussian process prediction closely matches the 14-track experiment for moderate depths, but fails at higher depths because the Verhaeghe model does not include all the necessary physics. This iterative approach using simple and complex simulations, combined with a surrogate model, reduces the computational cost of determining process parameters and forms the first steps towards uncertainty analysis and qualification of additively manufactured parts.

Figure 5. the predictions from a gaussian process surrogate built using depth from the verhaeghe model show good agreement with the experiments, except at depth greater than 150 µm, which is outside the range of interest.
Figure 5. The predictions from a Gaussian process surrogate built using depth from the Verhaeghe model show good agreement with the experiments, except at depth greater than 150 µm, which is outside the range of interest.
 

Impact on Mission

This research project supports the Laboratory’s mission in stockpile certification and core competency in advanced materials and manufacturing by developing a substantially improved, science-based approach to develop mature manufacturing technologies and systems in a rapid and cost-effective manner. By further developing stockpile stewardship capabilities in science-based manufacturing and additive process-aware simulation, accelerated qualification of additively manufactured components will be possible.

Conclusion

If a standard approach to qualification and certification were taken, then, over the 10-plus-year production lifecycle of a stockpile life-extension program, the production process would need to be “locked down” and nothing could evolve or improve without a rigorous process re-qualification. As a result, advances in a rapidly changing technology could not be implemented into production easily. Replacing the standard approach with integrated computational materials engineering would allow for translation of parameter and material data between various pieces of additive manufacturing equipment enabling production flexibility and scalability. Integrated computational materials engineering would provide geometry-aware, intelligent feed-forward capability which, when coupled with feedback control, will ensure “right every time” production or early automated rejection, thus minimizing risk.

As a result of this project, we have teamed with General Electric to respond to a broad agency announcement from the Office of Naval Research in Arlington, Virginia, for an expected $30-million, 3-year project called Quality Made, which focuses on accelerating the qualification of additively manufactured metals. We have active work-for-others agreements with Applied Materials in Santa Clara, California and KLA Tencor in Milpitas, California, and a collaboration with Northrup Grumman headquartered in Falls Church, Virginia, for a potential project for Naval Air Systems Command, headquartered in Patuxent River, Maryland.

References

  1. King, W., et al., "Overview of modelling and simulation of metal powder bed fusion process at Lawrence Livermore National Laboratory." Mater. Sci. Tech. 31(8), 957 (2015). LLNL-JRNL-656041. http://dx.doi.org/10.1179/1743284714Y.0000000728
  2. Boley, C., S. Khairallah, and A. Rubenchik, "Calculation of laser absorption by metal powders in additive manufacturing." Appl. Optic. 54(9), 2477 (2015). LLNL-JRNL-665313.
  3. Rubenchik, A., et al., "Direct measurements of temperature-dependent laser absorptivity of metal powders." Appl. Optic. 54(24), 7230 (2015).
  4. Rubenchik, A. M., et al., "Temperature-dependent 780-nm laser absorption by engineering grade aluminum, titanium, and steel alloy surfaces." Opt. Eng. 53(12), 122506 (2014).
  5. Khairallah, S. A., and A. Anderson, "Mesoscopic simulation model of selective laser melting of stainless steel powder." J. Mater. Process. Tech. 214(11), 2627 (2014). LLNL-JRNL-649602.
  6. Hodge, N. E., R. M. Ferencz, and J. M. Solberg, "Implementation of a thermomechanical model for the simulation of selective laser melting." Comput. Mech. 54(1), 33 (2014). LLNL-JRNL-647013.
  7. Eagar, T. W., and N. S. Tsai, "Temperature-fields produced by traveling distributed heat-sources." Weld. J. 62(12), S346 (1983).
  8. Kamath, C., et al., "Density of additively-manufactured, 316L SS parts using laser powder-bed fusion at powers up to 400 W." Int. J. Adv. Manuf. Tech. 74(1–4), 65 (2014). LLNL-TR-648000. http://dx.doi.org/10.1007/s00170-014-5954-9
  9. Verhaeghe, F., et al., "A pragmatic model for selective laser melting with evaporation." Acta Mater. 57(20), 6006 (2009).

Publications and Presentations

  • Boley, C., S. Khairallah, and A. Rubenchik, "Calculation of laser absorption by metal powders in additive manufacturing." Appl. Optic. 54(9), 2477 (2015). LLNL-JRNL-665313.
  • Boley, C. D., S. A. Khairallah, and A. M. Rubenchik, Modeling of powder absorption in additive manufacturing. CLEO: Applications and Technology, San Jose, CA, June 8–13, 2014. LLNL-PRES-648823.
  • Carlton, H. D., et al., "Damage evolution and failure mechanisms in additively manufactured stainless steel." Mater. Sci. Eng. 651, 406 (2015). LLNL-JRNL-672410. http://dx.doi:10.1016/j.msea.2015.10.073
  • Hodge, N., and R. Ferencz, Part-level finite element simulation of selective laser melting. 12th U.S. National Congress Computational Mechanics, Raleigh, NC, July 22–25, 2013. LLNL-ABS-618093.
  • Hodge, N., R. M. Ferencz, and J. M. Solberg, “Implementation of a thermomechanical model for the simulation of selective laser melting.” Comput. Mech. 54, 33 (2014). LLNL-JRNL-647013.
  • Kamath, C., Data mining and statistical inference in selective laser melting. (2015). LLNL-JRNL-674341-DRAFT.
  • Kamath, C., Data mining in materials science. Information Science for Materials Discovery and Design, Santa Fe, NM, Feb. 4–7, 2014. LLNL-ABS-643875.
  • Kamath, C., et al., "Density of additively-manufactured, 316L SS parts using laser powder-bed fusion at powers up to 400 W." Int. J. Adv. Manuf. Tech. 74(1-4), 65 (2014). LLNL-TR-648000. http://dx.doi.org/10.1007/s00170-014-5954-9
  • Khairallah, S. A., and A. Anderson, "Mesoscopic simulation model of selective laser melting of stainless steel powder." J. Mater. Process. Tech. 214(11), 2627 (2014). LLNL-JRNL-649602.
  • Khairallah, S., A. Anderson, and A. Rubenchik, Laser powder-bed fusion additive manufacturing: Effects of main physical processes on dynamical melt flow and pore formation from mesoscopic powder simulation. (2015). LLNL-JRNL-676495.
  • King, W. E., et al., Laser powder bed fusion additive manufacturing of metals; physics, computational, and materials challenges. (2015). LLNL-JRNL-676941.
  • King, W. E., et al., "Observation of keyhole-mode laser melting in laser powder-bed fusion additive manufacturing." J. Mater. Process. Tech. 214(12), 2915 (2014). LLNL-JRNL-642426. http://dx.doi.org/10.1016/j.jmatprotec.2014.06.005
  • King, W. E., et al., Observation of “keyhole mode” laser melting in laser powder bed fusion additive manufacturing. 24th Ann. Intl. Solid Freeform Fabrication Symp.—An Additive Manufacturing Conf., Austin, TX, Aug. 12, 2013. LLNL-ABS-636148.
  • King, W., et al., "Overview of modelling and simulation of metal powder bed fusion process at Lawrence Livermore National Laboratory." Mater. Sci. Tech. 31(8), 957 (2015). LLNL-JRNL-656041. http://dx.doi.org/10.1179/1743284714Y.0000000728
  • King, W. E., et al., Simulation and modeling of the metal laser powder bed fusion process to accelerate certification. Additive Manufacturing (AM) with Powder Metallurgy (PM) Conf., Orlando, FL, May 18–24, 2014. LLNL-ABS-644270.
  • McKeown, J. T., et al., "Rapidly solidified U-6wt%Nb powders for dispersion-type nuclear fuels." J. Nucl. Mater. 448, 72 (2014). LLNL-JRNL-645168.
  • Nourgaliev, R., et al., "Fully-implicit orthogonal reconstructed Discontinuous Galerkin method for fluid dynamics with phase change."J. Comput. Phys. 305, 964 (2015). LLNL-JRNL-669889.
  • Wu, A. S., et al., "An experimental investigation into additive manufacturing-induced residual stresses in 316L stainless steel." Metall. Mater. Trans. A 45, 6260 (2014). LLNL-JRNL-654740. http://dx.doi.org/10.1007/s11661-014-2549-x
  • Wu, A. S., et al., Effect of laser scanning pattern and build direction in additive manufacturing on anisotropy, porosity and residual stress. TMS 2013 142nd Ann. Mtg. and Exhibition, San Antonio, TX, Mar. 3–7, 2013. LLNL-ABS-640994.
  • Xia, Y., et al., "A third-order implicit discontinuous Galerkin method based on a Hermite WENO reconstruction for time-accurate solution of the compressible Navier–Stokes equations." Int. J. Numer. Meth. Fluid. 79(8), 416 (2015). LLNL-JRNL-669954.