Geoffrey Sanders (16-FS-024)
Abstract
Graph analytics extract meaningful information from the connections (edges) between entities (vertices) in relational data sets. Random walk models (a type of analytic) successfully address basic topological graph mining tasks such as ranking (e.g., Google’s PageRank) and clustering; however, they do not accommodate timestamps (the time at which an event is recorded by a computer) and other rich metadata (data that describes or summarizes data). Random walk models are thus insufficient for many dynamic graph-mining tasks of interest to the Laboratory. In this project, we developed random walk models with non-uniform edge transition probabilities biased towards desired graph substructure. Each “biased” walker stores and continually processes a small amount of temporal metadata, influencing its movement. We developed and analyzed a biased random walk dynamic graph ranking analytic that estimates the likelihood of all entities being influenced by a few known vertices, and we demonstrated this analytic’s efficacy to large volumes of real-world Wikipedia data on high-performance computing systems utilizing non-volatile random access memory. Our approach offers gains in efficiency (fewer operations and edge traversals), accuracy (precise temporal representation), and flexibility (more potential for user interaction). We forecast that this approach has better scalability than existing highly bulk-synchronous approaches (where all processes must wait for all other processes to complete the current computation phase before proceeding to the next phase) for a wide class of analytic tasks. This project affirms that biased random walk research is of significant Laboratory interest for data mining tasks of mission-relevance involving topology and diverse metadata at scale.
Background and Research Objectives
Often a data analyst has a few observations of known interest, but desires a more complete understanding of other observables that have influenced the known set. We note that when high-fidelity temporal metadata is available, timing information is often crucial to get the most reliable understanding of the data set. When the flow of information is a critical aspect of the data analysis at hand, temporal metadata is likely to be an important aspect for assessing the influence of one event on another. For instance, consider a network of journal publications linked explicitly by citations and implicitly with shared keywords or concepts. One may want to know which authors are the most influential to a group of articles and associated timing is fairly relevant to understand the directionality of influence in the implicit links. The situation is similar for understanding the influence of message authors in microblogging web services, like Twitter, where messages are mostly globally broadcast and not always explicitly linked, though they are implicitly linked via vocabulary, tags, and concepts. Without the temporal information, an analytic is likely to emphasize the largest and densest community. Consider a trending topic within a data set. One can see why this is highly problematic: An edge containing a concept that is gaining in popularity over time is influenced by edges of a small community, and the larger communities involved are likely full of more dependent edges. The timestamps are an easy way to filter many unrealistic answers to the question of which authors’ events were more influential within the topic.
Generally, analytics leveraging temporal metadata will outperform those that do not, and there are preexisting linear algebraic methods in the literature that do so1,2. However, these methods require the user to discretize time into epochs, which is the source of many drawbacks to these methods. First, for the user of these approaches to discover a suitable epoch size involves a large amount of exploratory data analysis. This is exacerbated in real-world data sets where different actors produce events at highly different rates and no single timescale may be appropriate for the analysis task. Second, these approaches introduce temporal artifacts, the most problematic of which being artificial uncertainty over which event in an epoch happened first. Other important artifacts happen at epoch boundaries, where two events close in time are put into different epochs. Additionally, the tensor-based approach described in Kolda and Bader’s work loses any notion of causality as tensor factorization is independent of permutation (of epochs)2. Approaches involving a sequence of linear systems such as described by Grindrod and Hingham can capture causality, but on a distributed high-performance computing system they require many bulk synchronous communication steps, one for each epoch1. Moreover distributed filtered matrix-vector multiplications would need to be developed for these approaches to be useful in high-performance computing environments.
In this project, our primary research goal was to explore the feasibility of developing a dynamic graph analysis framework that has high-fidelity representation of temporal information where subtle sequencing of events is respected and is implementable with a large amount of fine-grain parallelism. We selected biased random walk as a modeling solution that meets these needs and sought to demonstrate this clearly. We did so by designing an important dynamic graph ranking analytic, implementing the analytic within high-performance computing systems, and analyzing performance with a real-world data set of interest.
Scientific Approach and Accomplishments
Our feasibility study progressed in five major steps, each described below.
Analytic Design: Dynamic Graph Ranking
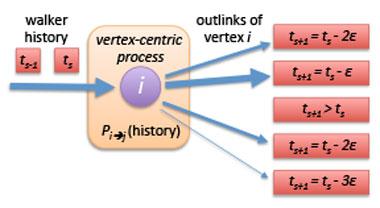
To design a biased random walk analytic to rank by influence, we adjusted the standard random walk model. Random walkers in the standard model have no memory of the edges they traverse; they merely sample outgoing edges uniformly. The long-term visitation statistics of the random walkers provide a ranking. We built a biased random walk model, where we give each walker individual memory of their last few traversals and allow them to bias the sampling of the next edge they traverse by factoring in their recent history. There is no need to discretize time, and a high-fidelity representation of the temporal metadata is used in analytics based off this model.
Specifically for our analytic, we use a dynamic walker model where the memory of each random walker is a clock. When a random walker traverses edge s it updates its clock to the associated timestamp ts (see Figure 1). Then the random walker policy is to follow a walk backwards in time: the probability of sampling the next out-going edge (s + 1) is zero if ts + 1 ≥ ts and is non-zero across edges for which ts + 1 < ts. For one version of this model the non-zero probabilities are uniform. The long-term visitation statistics of simulated biased random walkers provide a ranking. Alternatively, as depicted in Figure 1, the user can decide if they want the policy to be biased towards traversals with timestamps closer to ts, to model urgency for data sets where this is pertinent. Our vertex-centric simulation framework is highly flexible, and such important model adjustments are simple. On the other hand, these adjustments are not possible in the preexisting linear-algebraic approaches.
Data Curation: A Dynamic Wikipedia Graph
We curated the largest known openly available temporal graph data set from over 13 years of open source Wikipedia page-edit history. Wikipedia is a crowd-sourced encyclopedia that contains a collection of articles, editing discussion, categories, and images that are hyperlinked. Wikipedia’s content continues to expand and evolve by their public community of contributors. There are currently O(107) pages, O(106) editors, and O(109) edits. Storing the dynamic graph on disk requires 229GB in a compressed format. Edges represent the existence of hyperlinks between pages and have begin/end timestamps, [tb, te], (in seconds) corresponding to the creation and possible termination of the hyperlink. This data set served as our primary open test case for experimenting with temporal graph analytics. It was computationally intensive to curate the graph from the provided raw data from Wikipedia, so we have open-sourced the dynamic graph we have built and are sharing it with the broader research community at http://software.llnl.gov/havoqgt/datasets.html.
Experiments: Ranking Wikipedia Pages Dynamically by their Relation to Brad Pitt
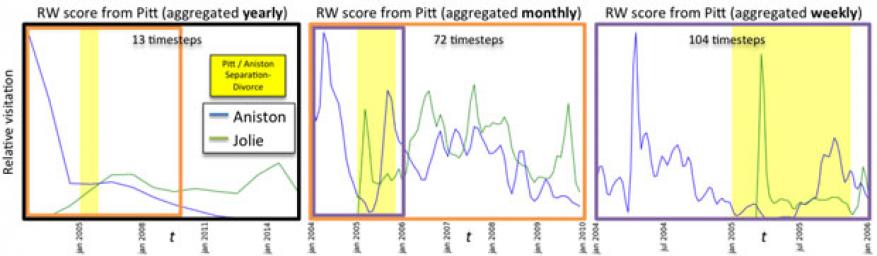
To demonstrate our dynamic ranking analytic, we chose a popular celebrity whose significant life events are well-known, so that we could examine Wikipedia connectivity over the course of time. Specifically, Brad Pitt was married to Jennifer Anniston at the onset of the data set; they were separated in January 2005 and divorced in October 2005. Mr. Pitt was dating Angelina Jolie shortly afterwards. This serves as an excellent prototype of an analyst using temporal graph ranking to narrow down the scope of follow-on analysis by focusing on events near critical changes in ranking.
In Figure 2, we present the output of our dynamic ranking analytic applied to Brad Pitt. The computation involved simulating 10 million biased random walkers and was done using Catalyst (a high-performance computer at Livermore) in 2 minutes with 768 processors. The figure has three different time-scales, each in a different plot, and all three come from the output of a single high-performance computing run. All three plots were built from the high-performance computer output on a serial machine using post-processing only. High-fidelity dynamics are visible. In the preexisting linear-algebraic approaches thousands of highly bulk-synchronous matrix-vector multiplications are required to see this level of fidelity, whereas our approach exploits a high-level of fine-grain parallelism. The implementation advances the team made sped this computation up 160 times, as described in the next section.
Software Development: Building Temporal Metadata Capabilities in HavoqGT
In support of performing temporal graph analytics on large graphs, we have extended a pre-existing graph framework called HavoqGT in several novel aspects2, 3. We added support for dynamic or temporal metadata, which allows edges to have begin/end timestamps associated with them. Additionally, this gives the capability to design biased random walk analytics that sample outgoing edges with probability as a function of the edge time stamps (as was done in the experiments in the previous section).
We identified a performance bottleneck when processing a large number of outgoing temporal edges, and designed temporal indexing data structures called interval-trees to accelerate the indexing of temporal edges. This indexing scheme was able to speed up a Wikipedia experiment involving 10 million biased random walks from 5.25 hours to under 2 minutes (160 times).
Finally, we began development of a strongly-typed graph that will allow users to model rich semantic metadata jointly with temporal metadata efficiently at scale.
Analysis: Predicting the Number of Walkers Required
During the summer of 2016, our research team developed an original theory that estimates how many sampled random walks are required to confidently observe a change in a dynamic ranking within a given time interval. This is important to understand the complexity involved in computing dynamic rankings and to understand what level of confidence we have in the rankings we compute. The theory will be further leveraged to be able to adaptively sample random walkers, focusing on periods of time where the ranking is more volatile. The results our team developed employ probability, statistics, and graph theory, including Chernoff Bounds and Markov chain analysis. We are currently writing them up with validating experiments for journal publication.
Impact on Mission
Our feasibility study supports Lawrence Livermore's core competency in high-performance computing, situation, and data science by enhancing the Laboratory's development of an advanced high-performance computing capability with the significant future application of cutting-edge graph-search technologies that meet diverse and rapidly changing data-analysis demands. These technologies have many applications in cyber security, space, and intelligence, and we are in a position to test novel graph-based analytics for discovering meaningful patterns or anomalies within mission-relevant data derived from unstructured information sources. For this reason, we believe this study will support strong programmatic interest in further high-performance computing graph mining research and development at Lawrence Livermore.
Maintaining cutting-edge graph capabilities with the computer science and mathematics expertise to build and use these technologies is of high strategic interest to the Laboratory. Through the student internship programs (Institute for Scientific Computing Research, Data Heroes, and Cyberdefenders), we had five student interns work on this project, directly or indirectly. It is highly likely that we will recruit two of these students as postdoctoral researchers at the Center for Applied Scientific Computing at Lawrence Livermore.
Conclusion
For this feasibility study, we developed a new graph analytic tool based on random walks biased with temporal metadata. Then we verified that the new analytic produces meaningful dynamic graph interpretation that is not efficiently attainable with previous analytics. Its success represents an important step towards a powerful new graph mining tool with potential for scalability to large volumes of data on modern high-performance computing resources. We argue that this class of techniques is more robust to noise, flexible to diverse and changing user demand, and efficient for high-performance computing resources. We have demonstrated these facts for a very simple class of dynamic graph ranking analytics. We developed these analytics using the HavoqGT graph library, building off previous asynchronous graph development at Lawrence Livermore. We evaluated our dynamic graph ranking analytic using an open-source dynamic Wikipedia graph that has similar challenges as mission-relevant customer data sets.
References
- Grindrod, P., and D. Higham, “A dynamical systems view of network centralit.” Proc. R. Soc. A, 470, 2165 (2014). http://doi.org/10.1098/rspa.2013.0835
- Kolda, T. G., and B. W. Bader, “Tensor decompositions and applications.” SIAM Rev. 51(3), 455 (2009). http://epubs.siam.org/doi/abs/10.1137/07070111X
- Pearce, R., M. Gokhale, and N. M. Amato, Scaling techniques for massive scale-free graphs in distributed (external) memory. 27th IEEE International Parallel and Distributed Processing Symp., Boston, MA, May 20–24, 2013. http://doi.org/10.1109/IPDPS.2013.72