1. Home
  2. Report Archives
  3. FY2016
  4. Nuclear, Chemical, and Isotopic Science and Technology
  5. Helium Age-Dating of Fuel-Cycle Materials for Nuclear Forensics

Helium Age-Dating of Fuel-Cycle Materials for Nuclear Forensics

Sean Gates (16-FS-025)

Abstract

Ascertaining the age and history of nuclear material is critical for forensic investigations and treaty verification. The process of radio-chronometry (measuring the ratio of parent–daughter radionuclides in a sample) constrains the time of production, purification, and processing of nuclear materials. We proposed to determine the feasibility of helium age-dating techniques for actinide metals. We investigated uranium-to-helium ages and helium diffusion kinetics obtained from a metallic, highly enriched uranium sample. The chemical and kinetic behavior of helium is sufficiently different than all other actinide-series daughter products that it may provide unique information on a sample’s history. As an inert gas that is readily lost from materials by heating, the uranium and plutonium–helium system is more likely to be reset during fuel-cycle processing than other uranium-series daughter isotopes. Therefore, the helium ages are more likely to reflect the time of most recent processing or purification. Coupling ages obtained from the helium chronometer with those from other chronometric systems may provide more precise constraints on the history of a forensic sample. We found that the average uranium-to-helium age for our experimental sample was 8% older than the known casting date, which indicates that excess helium was present, likely because of incomplete degassing of pre-existing helium during the casting process. Although the uranium-to-helium age is older than expected, the accuracy is comparable to other chronometers that have been applied to this material. Diffusion kinetics obtained from the uranium metal indicate that helium is quantitatively retained under plausible storage conditions.

Background and Research Objectives

Relating radiometric ages determined from measurements of parent–daughter isotopic systems to fuel-cycle processes is predicated upon two assumptions: the sample contained no daughter isotopes at the time of production, and parent or progeny isotopes were not exchanged with the environment since the production of the sample. If either of these assumptions is violated, then the calculated age will not reflect the production, purification, or processing age of the material. Radio-chronometers are an integral component of nuclear material forensic investigations.1,2 They provide constraints on the manufacturing and processing history of nuclear materials that may aid in attribution.2–6 For a chronometric system to yield an accurate age, two conditions must be satisfied. First, the daughter nuclides must be completely removed from the parent at the time of material production, and second, the daughter nuclides must be quantitatively retained after the production process.2 If these conditions are not met, the ages obtained from the chronometric analysis, termed model ages, may be spuriously old and young, respectively.

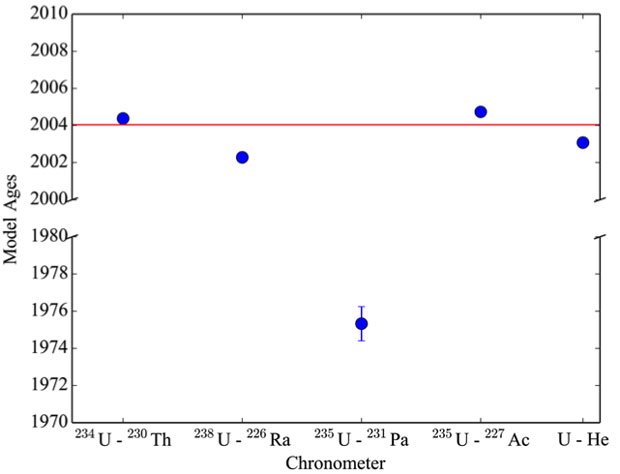
Because one does not a priori know whether an age calculated under these assumptions is meaningful, multiple chronometric systems are generally employed to examine samples of interest.7 For example, a past study analyzing highly enriched uranium metal from the International Technical Working Group Round Robin 3 (ITWG-RR3) exercise employed the uranium-234 → thorium-230, uranium-235 → protactinium-231, uranium-238 → radium-226, and uranium-235 → actinium-227 systems.8,9 It was found that the uranium-235 → protactinium-231 system yielded a significantly older age (approximately 30 years) than that determined from the other systems, all of which were within two years of the known casting date.8,9 Thus, the use of multiple actinide series chronometers provided constraints on the efficiency of daughter product segregation during the casting process, and enabled a more thorough understanding of the history of the sample, as well as increased confidence in significance of the age.9

The focus of our study was the development of an additional chronometer of relevance to nuclear forensics investigations: the uranium—helium system. While helium age dating is routinely utilized in Earth and planetary sciences to determine the ages of geologic phenomenon, this is the first time, to our knowledge, that the technique has been applied to fuel cycle materials.10 The chemical and kinetic behavior of helium is sufficiently different than all other actinide-series daughter products so that a uranium—helium chronometric system may provide distinctive information regarding the sample's history. As an inert gas with low solubility and high diffusivity, the uranium–helium system is more likely to be reset during fuel cycle processing than other uranium-series daughter isotopes.11 Therefore, it is reasonable to assume that uranium—helium ages are likely to reflect the time of most recent material processing, casting, or purification. Additionally, coupling the model ages obtained from the helium chronometer with those from other chronometric systems will enable more precise constraints on the history of a forensic sample and provide increased confidence in the determination of model ages.

In our study, we examined helium diffusion kinetics and uranium—helium ages obtained from a uranium metal used in the ITWG – RR3 exercise. We compared uranium—helium model ages obtained from these samples with other chronometric constraints on their ages and the known casting date, and used the diffusion kinetics to constrain the retentivity of helium under different storage conditions.

Scientific Approach and Accomplishments

Sample Description
A highly enriched uranium metal from the ITWG-RR3 exercise was selected for this study. The ITWG-RR3-B sample was obtained from a hollow cylindrical log (8.6-mm thick) that was cast from scrap uranium metal of unknown age on January 14, 2004. The uranium isotopic composition is shown in Table 1.8
Table 1. Uranium isotopic composition and associated uncertainties of the ITWG-RR3-B metal determined by inductively coupled plasma mass spectrometry.
Table 1. uranium isotopic composition and associated uncertainties of the itwg-rr3-b metal determined by inductively coupled plasma mass spectrometry.
Gas Analysis

Helium measurements were performed in the Livermore noble gas laboratory using a Nu Instruments Noblesse noble gas mass spectrometer equipped with six Faraday cup detectors and four ion-counting, discrete dynode multiplier detectors. Samples for analysis were encapsulated in high-purity platinum–iridium alloy tubes, placed under ultrahigh vacuum conditions and incrementally degassed using a feedback-controlled laser heating schedule. Samples were heated with a 75-W diode laser (λ = 970 nm) equipped with a co-axially aligned optical pyrometer for temperature control. The degassing schedule consisted of extractions at temperatures of 450 to 1300°C. In order to determine helium abundances, a calibrated helium-3 spike was introduced into the processing line during each heating step. In addition, helium mass discrimination was monitored throughout the course of the degassing experiment via bracketing analyses of a helium-3 and helium-4 standard. Isotope abundances were calculated at the time of admission into the mass spectrometer (t = 0), based upon polynomial regressions fit to the peak hopping scans. All heating steps and measurements used to determine the helium mass discrimination were corrected for system backgrounds.

In addition to the helium isotope measurements, argon-36 was measured to correct for any atmospheric contributions to helium-4. It was assumed that any atmospheric gases incorporated into the sample were not fractionated. To correct for any helium released from the platinum–iridium alloy packet, we gassed an empty packet degassed using the same heating schedule.

Model Age Determination

Model ages were calculated based on the sample mass, total abundance of degassed helium, and alpha production rate given by the uranium isotopic composition. All uncertainties are reported at two sigma and include propagated uncertainties from isotopic measurements, the helium-3 spike calibration, and the spectrometer mass discrimination. The uncertainty on the helium-3 spike calibration is approximately 0.7%. The uncertainty associated with the mass discrimination is 0.6%. Because these two sources of uncertainty are systematic, they are excluded from assessments of the reproducibility of the uranium—helium ages.

Alpha production is principally derived from the uranium-238, uranium-235, and uranium-232 decay chains. Uranium-233 and uranium-236 are also present in this sample, but their contribution is negligible given the concentrations and half-lives.

Calculation of Diffusion Kinetics

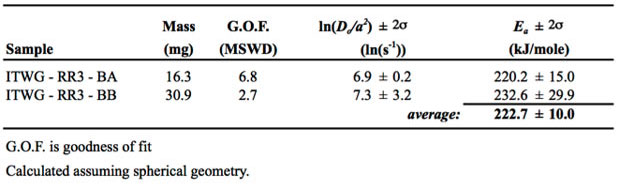
Diffusion coefficients normalized by the characteristic length scale (D/a2) were calculated for each heating step based upon the fraction of the total gas released and the extraction temperature and duration. We used Crank's equations for spherical geometry, following the algorithm of Fechtig and Kalbitzer.12,13 To determine the activation energy (Ea) for diffusion, we fit linear regressions to extractions that yielded reproducible D/a2 values during duplicate isothermal heating steps and the retrograde heating steps bracketed by these measurements.

The metal appears to contain a distribution of diffusion length scales, potentially related to fractures imparted during sample preparation or inherent defects, as discussed below. Thus, Arrhenius arrays calculated using the Fechtig and Kalbitzer algorithm, which assumes isotropic diffusion over a single length scale, are nonlinear13 (the Arrhenius equation is a formula describing the temperature dependence of reaction rates). Multi-domain diffusion models are required to reproduce the Arrhenius arrays and to simulate diffusive loss under environmental conditions of interest.14 Multi-domain diffusion modeling is predicated on the assumption that there exists a series of discrete distribution of diffusive length scales (domains) that are degassed simultaneously during the laboratory heating experiment. During the initial degassing stage, the Arrhenius diagrams (i.e., the calculated D/a2 values) predominately reflect gas lost from smaller domains. As degassing progresses, the Arrhenius plots increasingly reflect the kinetic characteristics of larger domains.

Diffusion Kinetics

Activation energies (Ea) and the frequency factors (Do) determined from linear regressions fit to the Arrhenius arrays are shown in Table 2 for two aliquots of the ITWG-RR3 material BA and BB. The metal yields reproducible Arrhenius arrays that define an average Ea of 222.7 ± 10.0 kJ/mol. This Ea is higher than that observed in lower-density uranium oxides.15

Table 2. Summary of uranium—helium diffusion parameters, including diffusion coefficients (D/a2) and activation energies (Ea).
Table 2. summary of uranium—helium diffusion parameters, including diffusion coefficients (<em>d/a</em><sup><sub>2</sub></sup>) and activation energies (<em>e<sub>a</sub></em>).

A multi-diffusion domain model using four domains was constructed to fit the ITWG-RR3-BA data (Figure 1). The multi-diffusion domain model indicates that approximately 98% of the helium is retained in the largest domain. The other domains are at least three orders of magnitude smaller in size and each contain 1% or less of the total helium. This model is consistent with surficial imperfections, perhaps related to sample preparation using a diamond saw, defining the small, volumetrically insignificant domains, and the bulk of the sample defining a single, cohesive domain.


Figure 1. arrhenius plot of the diffusion (<em>d/a</em><sup>2</sup>) of helium in the itwg-rr3-b uranium metal. orange dots indicate measured data. small blue dots along the solid blue line are multi-diffusion domain (mdd) model data. dashed blue lines represent the arrhenius arrays that describe diffusion in each of the four domains. relative domain sizes and gas fractionations are shown to the right of the figure.
Figure 1. Arrhenius plot of the diffusion (D/a2) of helium in the ITWG-RR3-B uranium metal. Orange dots indicate measured data. Small blue dots along the solid blue line are multi-diffusion domain (MDD) model data. Dashed blue lines represent the Arrhenius arrays that describe diffusion in each of the four domains. Relative domain sizes and gas fractionations are shown to the right of the figure.

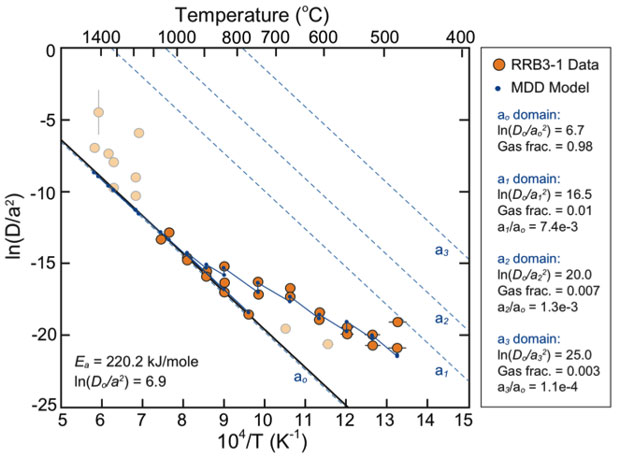
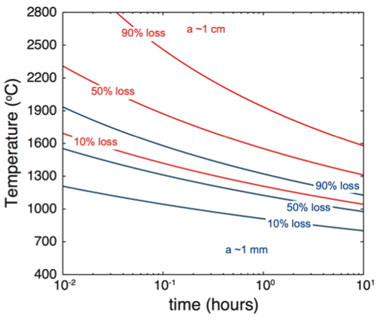
The diffusion kinetics inferred from the Arrhenius plot can be used to assess the sensitivity of the uranium—helium chronometer to thermal resetting. Fractional losses of helium that would result from square-pulse heating under different temperature-duration conditions are shown in Figure 2. Regardless of domain size, the uranium—helium system is resistant to resetting during long-term storage under environmental conditions. For example, the largest domain would only lose about 1% of its helium content if held at 400°C for 10 years. It thus appears that resetting of the chronometer requires a high-temperature thermal event such as casting.

Figure 2. fractional helium loss as a function of temperature and time.
Figure 2. Fractional helium loss as a function of temperature and time for the largest (ao) and smallest (a3) diffusion domains. These data indicate that uranium—helium would not be easily reset at standard environmental conditions.
 
Chronology

Two aliquots of the ITWG- RR3 material were analyzed, and the masses and helium abundances are detailed in Table 3. The uranium—helium model ages are shown alongside results from other chronometric systems in Table 4. The duplicate analyses yielded statistically indistinguishable helium concentrations. The weighted average uranium—helium age is January 27, 2003 ± 0.12 (internal) ± 0.23 (external) years, which is 0.96 ± 0.23 years older than the known casting date.

Table 3. Mass and the helium atomic content for the ITWG-RR3-B samples analyzed.
Table 3. mass and the helium atomic content for the itwg-rr3-b samples analyzed.

Table 4. Calculated model dates for the ITWG-RR3-B highly enriched uranium sample.
Table 4. calculated model dates for the itwg-rr3-b highly enriched uranium sample.
Comparison with Other ITWG-RR3-B Model Ages

Various chronometers have been applied to the ITWG-RR3-B sample, the results of which differ by approximately 30 years.9 Discordancy between chronometric systems has been attributed to incomplete segregation of some daughter products during casting. Specifically, thorium-230, actinium-230, and radium-226 yielded model ages broadly consistent with the known casting age of the ingot (within 19%). The observation indicates these daughters and granddaughters were efficiently removed from the uranium metal during the casting process.9 An anomalously old age was obtained with the uranium-235 → protactinium-231 chronometer, indicating protactinium-231 was incompletely removed from the metal during casting.9 The weighted average uranium—helium age (January 27, 2003 ± 84 days) is approximately a year older than the known casting date, which is consistent with a sample of an excess of 7 × 1013 atoms of helium per gram (see Figure 3).


Figure 3. model dates for the itwg-rr3-b highly enriched uranium sample.
Figure 3. Model dates for the ITWG-RR3-B highly enriched uranium sample. The uranium-234 → thorium-230, uranium-238 → radium-226, and uranium-235 → actinium-227 chronometers agree well with the known casting date shown as the red line. The uranium-235 → protactinium-231 chronometer indicated a model date significantly older than the casting date. The uranium—helium chronometer is approximately a year older than the casting date.

The most plausible source of the measured excess is helium that was incompletely degassed from the melt during casting. This excess helium may be derived from the scrap uranium melted for the casting or from outgassing of process components like the crucible or mold. Because the ITWG-RR3 sample was cast from scrap uranium metal from the year 1975 or earlier, helium has accumulated from at least 29 years of decay. By extrapolating the diffusion kinetics to higher temperatures, it is possible to estimate the duration for which the melt would have to be held at elevated temperatures to completely reset the chronometer. Under the assumption that the largest domain inferred from the multi-diffusion domain model (Figure 1) corresponds to approximately 1 mm (the macroscopic dimension of the samples analyzed), fractional losses of helium that would result from casting metals of different average dimensions (diffusive length scales) are shown in Figure 4. As previously detailed, the ITWG-RR3 scrap uranium was cast into cylinders with thicknesses on the scale of millimeters to centimeters. Typical casting conditions (e.g., temperatures of 1350 to 1450°C and maximum durations of 10 hours) appear insufficient to completely degas helium from melts of such length scales.16 Although there is considerable uncertainty in this analysis, and the duration and temperature conditions shown in Figure 4 likely represent upper bounds (assuming diffusivity in the melt is higher than that inferred from an upward extrapolation of the Arrhenius array), the retention of a few percent of pre-existing helium is evidently probable. Assuming an initial age of 1975 for the scrap metals, the measured excess of helium (7 × 1013 atoms/gram sample) corresponds to 2.5% retention during casting, which is consistent with the analysis outlined above. It is therefore reasonable to conclude that uranium—helium ages will be more accurate when metals are cast from young scraps and with increasing elapsed time since casting.

Figure 4. fractional helium loss as a function of temperature and time for a diffusion domain of size 1 mm (blue) and 1 cm (red). these data indicate that residual helium would likely be retained in the itwg-rr3 sample during the casting process.
Figure 4. Fractional helium loss as a function of temperature and time for a diffusion domain of size 1 mm (blue) and 1 cm (red). These data indicate that residual helium would likely be retained in the ITWG-RR3 sample during the casting process.

Impact on Mission

Livermore's capabilities in mass spectrometric techniques to analyze nuclear samples are significant. A helium chronometer would provide novel insights into the recent use of a sample under investigation, and has the potential to become a standard chronometric method in nuclear forensic analysis. This feasibility study, therefore, supports the nuclear, chemical, and isotopic science and technology core competency and would enhance the Laboratory's ability to analyze nuclear forensic samples. Our research supported this competency by developing a uranium—helium chronometer that provided novel insights into the recent use of the ITWG-RR3 sample and that has the potential to become a standard chronometric method for nuclear forensic applications. In addition, the further development of this chronometer will likely result in enhanced collaboration and synergies with other groups.

Conclusion

The uranium—helium chronometric system was applied to milligram-sized fragments taken from a highly enriched uranium ingot. The uranium—helium model age for this sample is within a year of the known purification date, but it appears to contain excess helium. Diffusion kinetics inferred from the incremental degassing experiments indicate that incomplete degassing of helium present in the melt during the casting process is likely the source of excess helium. Additionally, the diffusion data demonstrate that the uranium—helium chronometric system is unlikely to be reset unless exposed to a high-temperature (>500°C) processing event for a significant time duration (years). Coupling this chronometer with those previously employed for nuclear forensic applications will aid in the interpretation of unknown samples, as well as in the understanding of nuclide behavior in uranium metal during processing and purification events. We plan on expanding this work to uranium oxide and plutonium samples, and we are submitting proposals to establish the uranium—helium chronometer as a standard method in the analysis of nuclear forensic materials.

References

  1. Moody, K. J., P. M. Grant, and I. D. Hutcheon, Nuclear forensic analysis. CRC Press, Boca Raton, Florida (2014).
  2. Mayer, K., M. Wallenius, and Z. Varga, "Nuclear forensic science: Correlating measurable material parameters to the history of nuclear material." Chem. Rev. 113(2), 884 (2013). http://dx.doi.org/10.1021/cr300273f
  3. Varga, Z., and G. Surányi, "Production date determination of uranium-oxide materials by inductively coupled plasma mass spectrometry." Anal. Chim. Acta 599(1), 16 (2007). http://dx.doi.org/10.1016/j.aca.2007.07.069
  4. Varga, Z., M. Wallenius, and K. Mayer, "Age determination of uranium samples by inductively coupled plasma mass spectrometry using direct measurement and spectral deconvolution." J. Anal. At. Spectrom. 25(12), 1958 (2010). http://dx.doi.org/10.1039/C0JA00048E
  5. Williams, R. W., and A. M. Gaffney, "230Th-234U model ages of some uranium standard reference materials." Proc. Radiochim. Acta 1, 31 (2011).
  6. Eppich, G. R., et al., "235U–231Pa age dating of uranium materials for nuclear forensic investigations." J. Anal. At. Spectrom. 28(5), 666 (2013). http://dx.doi.org/10.1039/C3JA50041A
  7. Kristo, M. J., et al., "Nuclear forensic science: Analysis of nuclear material out of regulatory control." Ann. Rev. Earth Planet. Sci. 44, 555 (2016). http://dx.doi.org/10.1146/annurev-earth-060115-012309
  8. Nuclear Forensics International Technical Working Group (ITWG), Round robin 3 exercise after action and lessons learned report. Coordinator, R. Hanlen. Pacific Northwest National Laboratory, Richland, WA (2011). PNNL–20079.
  9. Kayzar, T. M., and R. W. Williams, "Developing 226Ra and 227Ac age-dating techniques for nuclear forensics to gain insight from concordant and non-concordant radiochronometers." J. Radioanal. Nucl. Chem. 307(3), 2061 (2016). http://dx.doi.org/10.1007/s10967-015-4435-4
  10. Farley, K. A., "(U–Th)/He dating: Techniques, calibrations, and applications." Rev. Mineral Geochem. 47(1), 819 (2002). http://dx.doi.org/10.2138/rmg.2002.47.18
  11. Trinkaus, H., and B. N. Singh, "Helium accumulation in metals during irradiation—Where do we stand?" J. Nucl. Mater. 323(2–3), 229 (2003). http://dx.doi.org/10.1016/j.jnucmat.2003.09.001
  12. Crank, J., The Mathematics of diffusion, second edition. Clarendon Press, Oxford, United Kingdom (1975).
  13. Fechtig, H., and S. Kalbitzer, "The diffusion of argon in potassium-bearing solids." Potassium argon dating, Springer Verlag, Berlin, Germany (1966).
  14. Lovera, O. M., F. M. Richter, and T. M. Harrison, "The 40Ar/39Ar thermochronometry for slowly cooled samples having a distribution of diffusion domain sizes." J. Geophys. Res. 94(B12), 17917 (1989). http://dx.doi.org/10.1029/JB094iB12p17917
  15. Roudil, D., et al., "Diffusion of radiogenic helium in natural uranium oxides." J. Nucl. Mater. 378(1), 70 (2008). http://dx.doi.org/10.1016/j.jnucmat.2008.05.001
  16. Ripley, E. B., Uranium processing and properties. Springer, New York (2013).