Scalable High-Order Computational Multiphysics at Extreme Scale

Charles Still (14-SI-002)

Abstract

Our goal was to enable a new breed of computational physics algorithms that improved simulation quality and mapped better onto future computing architectures. We accomplished this goal through a multi-disciplinary team consisting of computational mathematicians, computational physicists, and computer scientists. Significant achievements include extending the high-order Lagrangian hydrodynamics code to include a multi-material remap phase producing an arbitrary Lagrangian–Eulerian hydrodynamics capability. We then coupled this hydrodynamics code to a newly developed thermal radiation package producing a radiation hydrodynamics capability, which is the main building block to modeling Inertial Confinement Fusion experiments. Simulation results from this new code produce more accurate answers than previous low-order codes with improved symmetry preservation and fewer remap steps reducing numerical diffusion. Complementary computer science and algorithm design work refactored the Lagrangian hydrodynamics solver to rely on a matrix-free formulation. Changing to matrix-free solvers increases the number of floating-point operations, while reducing the memory footprint and data motion needs. With memory capacity and bandwidth growing slower than floating-point operation rates, these changes result in a code that will map well to future computer architectures. We transitioned all of these capabilities to Livermore's Advanced Simulation Computing program, which is continuing to fund the BLAST high-order finite-element hydrodynamics software as part of the next-generation simulation code MARBL, which is a new multiphysics application code for simulating high-energy-density physics and focused experiments driven by high-explosive, magnetic, or laser-based energy sources

Background and Research Objectives

Simulation via high-performance computing is an essential cross-cutting capability of the Laboratory. Multiphysics simulation capabilities are important to predictive science and are used in many important Laboratory programs, such as the National Ignition Facility (NIF). Most multiphysics simulation tools were developed in an era when floating-point operations were the performance-limiting factor. However, data motion and memory capacity are now the limiting factors because energy considerations are driving the design of high-performance computing architectures. This effectively inverts the computing model used for the design of many current codes. Additionally, low-order production codes that were initially designed decades ago do not capture certain simulation features as accurately as desired. High-order algorithms offer the opportunity to both produce more accurate simulations while more efficiently using current and future high performance computers. Our goal was to establish a new breed of multiphysics simulation capabilities based on high-order, finite-element formulations, where algorithms are designed from inception to take advantage of future hardware features. To accomplish this goal, we focused on developing coupled high-order, finite-element numerical methods for multiphysics simulations involving arbitrary Lagrangian––Eulerian hydrodynamics (a mathematical description of fluid flow in a shocked substance), multigroup radiation-diffusion, and magneto-hydrodynamics. This numerical algorithm development was complemented with a computer science research effort to show that the high-order simulation technology is scalable, well-suited to advanced extreme-scale architectures, and offers multiphysics modeling capabilities superior to current algorithms.

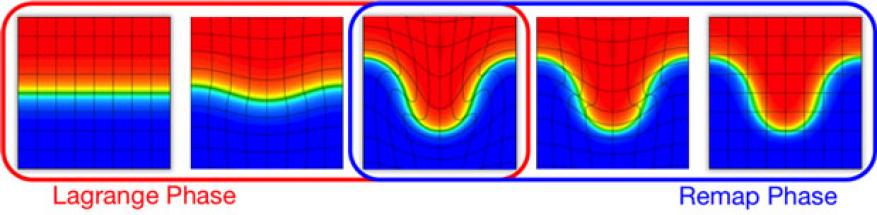
The arbitrary Lagrangian–Eulerian framework forms the basis of many large-scale multimaterial shock hydrodynamics and multiphysics codes. We focused on the so-called two-stage approach, which consisted of a Lagrange phase, where the hydrodynamics equations were solved on a moving mesh, followed by a remesh/remap phase, where a better mesh was derived and all fields were moved to this new mesh, as shown in Figure 1.

Our overall research objective was to produce a first-ever, high-order, arbitrary, Langrangian–Eulerian, radiation shock-hydrodynamic, multi-physics simulation capability that is able to more effectively exploit current and future computer architectures than today’s low-order codes. Within the project, various mathematics, computational physics, and computer science objectives contributed to fulfilling the larger project goal.

The mathematical research objective was to provide additional arbitrary Langrangian–Eulerian capabilities to the existing high-order finite element discretizations for Lagrangian hydrodynamics which had already been derived.^1–3 These methods have (1) demonstrable ability to more accurately capture geometrical features of a flow region and maintain robustness with respect to mesh motion using curvilinear zones and high-order bases; (2) significant improvements in symmetry preservation for symmetric flows; (3) sharper resolution of a shock front for a given mesh resolution including the ability to represent a shock within a single zone; (4) substantial reduction of mesh imprinting for shock wave propagation not aligned with the computational mesh; (5) higher than second-order convergence in smooth regions; and (6) the necessary flexibility to achieve the latter benefits in both axisymmetric geometry and for elastic-plastic materials.

The first desired addition was the ability to represent and robustly evolve materials with different properties. Multi-material arbitrary Langrangian–Eulerian simulations inevitably develop cells containing multiple materials, where so-called closure models are needed to define material evolution in a physically reasonable way. For some problems, such as high velocity impacts, the lack of such methods results in unphysical sound speeds, which cause prohibitively small time steps. Another requirement was the ability to relax high-order curvilinear meshes. The goals of this optimization step were to improve the mesh from an approximation point of view, to relax the time-step constraints, and to avoid mesh tangling and element inversion. Once we developed the Lagrangian and remesh phases, the next objective became the remap phase, where the state variables were transferred from the old mesh to the new mesh. This remap process had to be both high-order accurate and monotone—not generating any new extrema—which could only be achieved by nonlinear methods. The final objective was the inclusion of additional physics, namely, coupling to the equations of radiation diffusion. These equations introduced additional nonlinear and implicit terms in the system. The project goal was for BLAST, a finite-elements code for shock hydrodynamics, to be able to perform robustly full arbitrary Langrangian–Eulerian simulations of highly deforming materials with different properties, and in particular, materials emitting thermal radiation.

The computer science research objective was to determine if high-order methods are a promising path for more effectively using current and future computer architectures. We investigated multiple research questions: How do we evaluate if a good mapping onto a future architecture is possible? What performance optimizations are needed to implement this mapping? What are the tradeoffs of using high-order methods relative to low-order methods?

Scientific Approach and Accomplishments

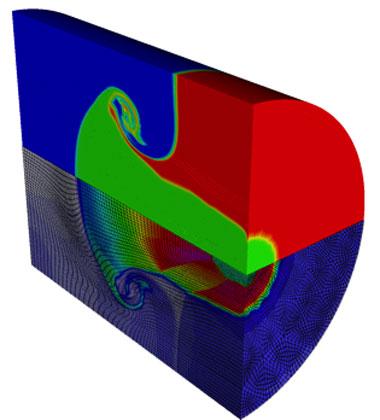
We fulfilled project expectations by deriving a novel closure model for high-order finite element multi-material hydrodynamics; defining new approaches for monotone remap of high-order finite element scalar fields on curvilinear meshes, which were later extended for the case of polynomial orders higher than three; presenting a complete, arbitrary Langrangian–Eulerian framework for the full multi-material Euler system; and demonstrating the ability to perform non-trivial, full, arbitrary Langrangian–Eulerian radiation hydrodynamics simulations as shown in Figures 2 and 3.^4–7

Major Research Directions and Developments

Technical details about each of the major research directions are presented in the following sections. All these concepts were incorporated in the BLAST code, allowing its current capabilities to perform multi-material, arbritary Lagrangian-Eulerian radiation hydrodynamics simulations.

Closure Model

We developed a new closure model algorithm compatible with high-order finite element discretizations. The goal of such models is to define the extra quantities, which appear in the system when one considers the multi-material Euler equations. The method defined a specific pressure equilibration approach to achieve sub-cell resolution without any knowledge of explicit material interfaces. Volume fractions were represented as general finite element functions, and evolved at integration points by a partial noninstantaneous pressure equilibration procedure. The full pressure equilibration was achieved by the combined action of the closure model and hydrodynamic motion. Each material’s specific internal energy equation used its own materials pressure, and an energy exchange term was introduced to account for the volume fraction changes. This internal energy exchange was determined so that every material produced positive entropy, and the total entropy production was maximized in compression and minimized in expansion. Artificial viscosity was computed for each material and used in the corresponding internal energy equation with appropriate scaling. All material viscosities were summed to form the total momentum viscosity. The resulting model was defined on a continuous level (that is, it was embedded in the starting equations), which made it independent of space and time discretization. The model was validated on both standard benchmark problems and more challenging two-dimensional and three-dimensional high-velocity impact tests with more than two materials.⁴

Curvilinear Mesh Relaxation

We relaxed the high-order meshes in BLAST via node movement such that the topology of the mesh did not change during the remesh phase. Various methods were derived and tested, including the generalization of the classical harmonic smoothing to high-order meshes via appropriately defined mesh Laplacian operators; non-linear techniques formulating the relaxation process as an integral minimization problem; and relaxation based on solving an elasticity type problem. The most commonly used relaxation technique was the newly developed diffusion relaxation, which was based on solving a high-order elliptic equation that represented the change in mesh positions. This method performed best with respect to some defects that resulted from the fact that some mesh relaxers treated vertex nodes in high-order meshes differently than the other nodes.

We addressed the remap procedure by formulating a continuous advection equation that transported the state variables between the Lagrangian and optimized meshes over a fictitious time interval so that the variables didn’t change with respect to the Eulerian frame of reference. The initial efforts resulted in a high-order, finite-element, discontinuous-Galerkin formulation that could be combined with a nonlinear monotonicity approach. We derived three such nonlinear approaches: (1) locally scaled diffusion, which defined local lumping of the mass matrices and upwinding of the advection matrices using an iterative process and a local monotonicity measure; (2) optimization based remap, which was based on an optimization procedure that enforced monotonicity and conservation in the remapped fields; and (3) a particular flux-corrected transport-based approach, which was a high-order, finite element generalization of the classical flux-corrected transport method.⁵

While the above methods were satisfactory up to third-order finite elements, additional effort was needed to reduce local oscillations resulting from higher polynomial orders. To address that issue, we derived the element-based, flux-corrected transport method, which modified the original flux-corrected transport method by adding (1) the concepts of localized bounds lookup, (2) correction of the high-order solution only at places where it violated the required bounds, and (3) zone-based, non-linear mass corrections.⁶

Because the remap evolved the conservative fields, such as mass, while preservation of bounds was imposed with respect to the primal fields, such as density, additional routines were derived to synchronize the monotonicity processing. The flux corrected transport based approach was altered by defining a ”compatible” low-order solution, which was both conservative and monotone with respect to the primal field and material of interest. The flux-corrected transport fluxes were also modified to take into consideration the primal field bounds. Similar methods were used for the projections between the conservative and primal fields, which were performed between each Lagrangian and remap phase.⁷

Radiation Hydrodynamics

The first additional physics added to BLAST was propagation of thermal radiation. The chosen model was the flux formulation of the single group radiation diffusion equations coupled to the hydrodynamics. The additional radiation energy field is discretized in the same space as the material’s internal energy, that is, L2, while the radiation flux is in the Hilbert space H(div). Because the resulting system is nonlinear, we initially developed a Newton-based method followed by a more involved block Gauss-Seidel type method, which alternates between solving zone-based nonlinear problems and solving a global linear system. The block Gauss-Seidel method is well suited for future extension to the multi-group radiation approximation and for graphics processing unit architectures, which excel at zone-based dense linear algebra kernels. Both methods ultimately result in a linear system for the Hilbert space H(div), where the hybridization and static condensation techniques are utilized. Finally, we developed an implicit-explicit, total energy conservative second-order time integrator.

Algorithm changes and performance optimization

More accurate simulation results are not useful unless they can be achieved in a reasonable amount of time. To compliment the new mathematical model development efforts, our computer science team analyzed and optimized the BLAST code. While much of the optimization work was computer-science-centric, tight coupling with the rest of the project was required as the analysis often showed that new, more scalable solver methodologies were needed. In addition to comparing BLAST against itself, we compared BLAST to current production codes, in particular Ares. The goal was to demonstrate not only improvements to BLAST, but that high-order results could be produced without a significant increase in runtime.⁸

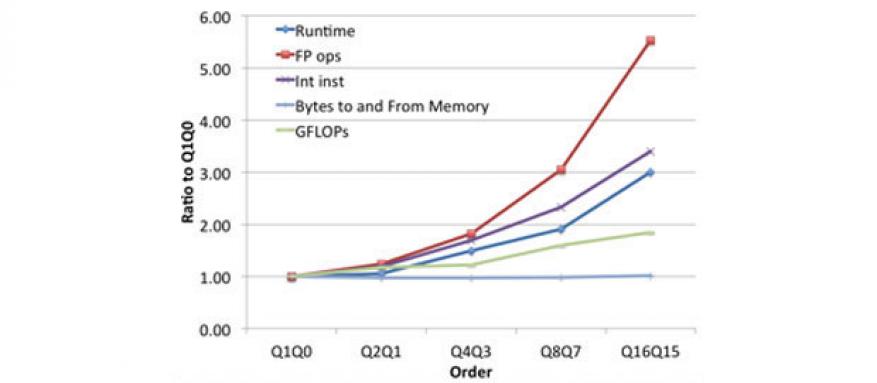
Profiling work focused on data motion needs showed that BLAST required about 25x more data motion than Ares, with the gap growing higher with order. The first significant algorithm change to address this problem involved switching from an assembled matrix solver format to a partially assembled, matrix-free solver. The resulting shift reduced data motion by 5x for order Q2Q1 with larger reductions at higher order. The matrix-free solver has order-independent data motion needs as shown in Figure 4. Accompanying the decrease in data motion was an increase in floating-point operations, which will be relatively cheaper on future machines.

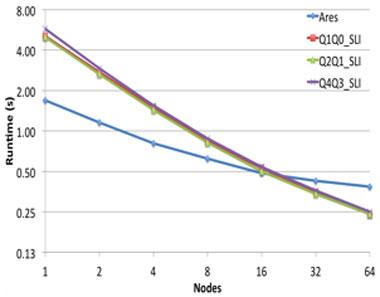
However, after these changes, BLAST still required about 5x the data motion as Ares. Further reduction was required to shrink the data motion of the matrix solver, which still consumed over 80% of the data motion. We reduced the solve cost by switching from a conjugate gradient solver, which is often used as an iterative algorithm for sparse systems too large to be handled by a direct implementation or other direct methods, to a stationary linear iteration solver with a fixed iteration count. While conjugate gradient is typically a faster solver for hydrodynamics problems where information propagates slowly across the mesh, in our case, stationary linear iteration was sufficient. This switch also reduced the number of global synchronization operations. Figure 5 shows the results of this change that, paired with optimizations to further improve the performance of BLAST, resulted in a code able to strong-scale better and outperform Ares on some problems.

The BLAST optimization work resulted in significant speedups, but there is still room for further improvement. Research into leveraging libraries to speed up the small matrix operations that occur throughout BLAST showed that none of the freely available open source packages were suitable for our needs.⁹ However, the Advanced Simulation Computing program is now funding an ongoing effort to help develop optimized library routines for advanced architectures that BLAST can leverage.¹⁰

Collaborative Code Modeling and System Noise Reductions

We worked with collaborators at the Laboratory and other institutions to better understand BLAST and leverage BLAST knowledge for other work. Collaborations with performance modeling researchers produced models of BLAST that help explain its performance and was used to gain new insights into its communication behavior.¹¹ Mutually beneficial collaborations with systems researchers focused on reducing system noise.¹² We leveraged their experiments to better understand BLAST scalability challenges while providing application expertise. These experiments have led to different default system configurations for our new clusters at Livermore that will improve the performance of many applications at scale.

Impact on Mission

Developing improved multiphysics codes are central to the Laboratory's strategic focus area in stockpile stewardship science. Our goal was to demonstrate a new simulation capability——a scalable, high-order, coupled multiphysics simulation——through development of a performance-portable code designed to work well on emerging advanced architectures that will form the basis for the technology platforms of Livermore's Advanced Simulation and Computing (ASC) Program. The mathematical and computer science work on the project demonstrated the first-ever high-order multiphysics arbitrary Lagrangian-Eulerian algorithms, establishing their feasibility as a promising discretization technology for next-generation computing architectures. The project also had a positive staffing impact: Both postdocs hired to work on this project have been converted to permanent positions. Our research supported the core competency in high-performance computing, simulation, and data science to simulate the behavior and performance of complex systems and expanding capabilities to exascale computing and beyond.

Conclusion

We developed a new multi-material arbitrary Lagrangian-Eulerian radiation hydrodynamics capability and showed it can run efficiently on future computer hardware. We also developed new methods for multi-material closure models, curvilinear mesh relaxation, monotone and synchronized remap of high-order finite element fields, and radiation diffusion. Matrix-free solver implementations and computer science optimizations resulted in performance improvements of up to 12x, while minimizing data motion. All of these improvements were implemented in the BLAST code, which demonstrates improved symmetry preservation and less numerical diffusion than previous low order codes. We demonstrated that the high-order approach can be a win-win situation, delivering better results while also better utilizing available high-performance computing resources. The new algorithms have transitioned to the programs for further development in the newly established MARBL code. The Laboratory's Advanced Simulation Computing Program is continuing to develop BLAST as part of its Multiphysics on Advanced Platforms Project.

References

1. Dobrev, V. A., T. V. Kolev, and R. N. Rieben, "High-order curvilinear finite element methods for Lagrangian hydrodynamics." SIAM J. Sci. Comp. 34(5), B606 (2012). http://dx.doi.org/10.1137/120864672
2. Dobrev, V. A., et al., "High-order curvilinear finite elements for axisymmetric Lagrangian hydrodynamics." Comput. Fluid. 83, 53 (2013). http://dx.doi.org/10.1016/j.compfluid.2012.06.004
3. Dobrev, V. A., T. V. Kolev, and R. N. Rieben, "High order curvilinear finite elements for elastic–plastic Lagrangian dynamics." J. Comput. Phys. 257(Part B), 1062 (2014). http://dx.doi.org/10.1016/j.jcp.2013.01.015
4. Dobrev, V. A., et al., "Multi-material closure model for high-order finite element Lagrangian hydrodynamics." Int. J. Numer. Meth. Fluid. 82(10) (2016). http://dx.doi.org/10.1002/fld.4236
5. Anderson, R. W., et al., "Monotonicity in high-order curvilinear finite element arbitrary Lagrangian-Eulerian remap." Int. J. Numer. Meth. Fluid. 77(5), 249 (2014). http://dx.doi.org/10.1002/fld.3965
6. Anderson, R. W., et al., "High-order local maximum principle preserving (MPP) discontinuous Galerkin finite element method for the transport equation." J. Comput. Phys. In review (2016).
7. Anderson, R. W., et al., High-order ALE multi-material hydrodynamics. (2016). LLNL-JRNL-706339.
8. Langer, S. H., et al., Performance analysis and optimization for BLAST, a high order finite element hydro code. NECDC 2014, Los Alamos, NM, Oct. 20–24, 2014. LLNL-PROC-666382.
9. Motter, P., I. Karlin, and C. Earl. BLAST motivated small dense linear algebra library comparison. Intl. Conf. High Performance Computing, Networking, Storage and Analysis, Austin, TX, Nov. 15–20, 2015. LLNL-ABS-676191.
10. Abdelfattah, A.,et al., "High-performance tensor contractions for GPUs." Procedia Comput. Sci. 80, 108 (2016). http://dx.doi.org/10.1016/j.procs.2016.05.302
11. Calotoiu, A., et al., Fast Multi-Parameter Performance Modeling. 2016 IEEE Intl. Conf. Cluster Computing (CLUSTER), Taipei, Taiwan, Sept. 13–15, 2016. http://dx.doi.org/10.1109/CLUSTER.2016.57
12. León, E. A., I. Karlin, and A. T. Moody, "System noise revisited: Enabling application scalability and reproducibility with SMT." 2016 IEEE Intl. Parallel and Distributed Processing Symp. (IPDPS) (2016). http://dx.doi.org/10.1109/IPDPS.2016.48

Publications and Presentations

• Anderson, R. W., et al., High-order ALE multi-material hydrodynamics. (2016). LLNL-JRNL-706339.
• Brunner, T. A., et al., High-order finite element Lagrangian hydrodynamics with radiation diffusion. (2015). LLNL-PRES-670726.
• Brunner, T. A., Preserving positivity of solutions to the diffusion equation for higher-order finite elements in under-resolved regions. Joint Intl. Conf. Mathematics and Computation (M&C), Supercomputing in Nuclear Applications (SNA) and the Monte Carlo (MC) Method, Nashville, TN, Apr. 19–23, 2015. LLNL-PROC-666744.
• Brunner, T. A., Preserving solution positivity of higher-order finite elements in under-resolved regions. (2015). LLNL-POST-669774.
• Dobrev, V. A., et al., Multi-material remap algorithms for high-order ALE simulations. (2015). LLNL-PRES-676869.
• Dobrev, V. A., et al., Multi-material remap algorithms for high-order ALE simulations. (2015). LLNL-PRES-675172.
• Dobrev, V., et al., Scalable high-order multi-material ALE simulations. (2015). LLNL-POST-676385.
• Earl, C., et al., BLAST computer science update. (2016).LLNL-PRES-681475.
• Haidar, A., et al., Accelerating tensor contractions for high-order FEM on CPUs, GPUs, and KNLs. (2016). LLNL-POST-701583.
• Karlin, I., Blast performance analysis and improvements. (2015). LLNL-PRES-666564.
• Karlin, I., Future architecture influenced algorithm changes and portability evaluation using BLAST. (2016). LLNL-PRES-690242.
• Karlin, I., How advanced architectures are affecting our applications. (2015). LLNL-PRES-674213.
• Karlin, I., Understanding present application performance to prepare for the future. (2015). LLNL-PRES-668388.
• Karlin, I., and T. Kolev, BLAST. (2016). LLNL-PRES-679758.
• Karlin, I., et al., Performance, power, and resilience tradeoffs in algorithmic design. Workshop on Modeling & Simulation of Systems and Applications, Seattle, WA, Aug. 12–14, 2015. LLNL-PRES-676255.
• Kolev, T., Hydro algorithms, part 1: High-order finite elements. (2016). LLNL-PRES-683561.
• Langer, S. H., et al., Performance analysis and optimization for BLAST, a high order finite element hydro code. (2016). LLNL-PRES-661954.
• Motter, P., I. Karlin, and C. Earl. BLAST motivated small dense linear algebra library comparison. Intl. Conf. High Performance Computing, Networking, Storage and Analysis, Austin, TX, Nov. 15–20, 2015. LLNL-ABS-676191.
• Langer, S. H., et al., Performance analysis and optimization for blast, a high order finite element hydro code. Nuclear Explosive Code Development Conf., Los Alamos, NM, Oct. 20–24, 2014. LLNL-PROC-666382.
• Motter, P., I. Karlin, and C. Earl, BLAST motivated small dense linear algebra library comparison. SC15, Austin, TX, Nov. 15–20, 2015. LLNL-POST-676190.
• Quezada de Luna, M., and V. Z. Tomov, 2015. Non-oscillatory flux corrected transport for high-order finite element discretizations. (2015). LLNL-POST-675658.
• Tomov, V. Z., Closure models for high-order finite element hydrodynamics. (2015). LLNL-PRES-675018.
• Tomov, V. Z., Handling multiple materials with high-order finite elements. (2015). LLNL-PRES-672616.
• Tomov, V. Z., High-order methods for multi-physics multi-material ALE in BLAST. (2015). LLNL-POST-677578.
• Tomov, V. Z., Multi-material ALE and radiation coupling in BLAST. (2016). LLNL-PRES-687424.
• Tomov, V. Z., Multi-material ALE in the BLAST Code. (2015). LLNL-PRES-668352.