Deepak Rajan (15-ERD-041)
Abstract
In this project, we have developed specialized algorithms to analyze power-grid optimization problems in the presence of uncertainty. Real-world problems are typically too large to be solved directly and require the development of specialized decomposition schemes that can leverage high-performance computing (HPC) architectures. We focus on discrete optimization problems (i.e., problems with integer-valued decisions), since these are extremely common in the power grid. This class of optimization problems is referred to as mixed-integer programs (MIPs). When some of the parameters or data are random, optimization problems can be extended to handle uncertainty in the model by generating many possible instantiations of the model, called "scenarios."
We consider two main kinds of decomposition schemes to solve stochastic mixed-integer programs (SMIPs): branch and bound (B&B) decomposition schemes, and Scenario-Decomposition schemes. In the first, we present some new ideas and algorithms to solve such problems by developing parallel algorithms that leverage HPC architectures. In the second, we develop new parallel-implementation ideas and new theoretical approaches for accelerating the performance of any scenario-decomposition scheme. We present results demonstrating the effectiveness of our approach on stochastic optimization test instances from the Stochastic Integer Programming Library (SIPLIB), and on real-world stochastic power grid planning problems, such as stochastic unit commitment.
Background and Research Objectives
Electricity-production modeling and simulation tools are used extensively by utilities, independent system operators, state utility commissions, and oversight agencies to support major policy and acquisition decisions for the nation's power grid. Grid-production simulation models attempt to capture the cost-minimizing behaviors of grid operations. As such, they are fundamentally optimization models with decision and state variables representing power plant output, energy storage levels, and power flows in transmission lines for each time period. Due to the presence of state variables, these optimization models belong to the class of optimization problems known as MIPs. To incorporate uncertainty, the model is usually approximated with a pre-defined number of possible realizations (called samples or scenarios), resulting in SMIPs. Higher-resolution models (i.e., those incorporating more scenarios to represent the uncertainty) require more decision variables and constraints. As a result, production-cost simulations are computationally intensive.
This project addresses one important technology gap in production-simulation tools: the need for solving larger models, primarily resulting from the incorporation of uncertainty into the tools. The project developed scalable algorithms and techniques that advance our ability to solve Stochastic MIPs. In the past, stochastic grid models were simplified and implemented with far fewer scenarios to ease the computational burden in order to provide answers in a timely manner to inform decision processes. This gap in planning capabilities has been recognized by independent system operators (ISOs) and utility-grid planners. Our approach to scaling such large-scale stochastic optimization problems is to exploit problem structure and decompose by scenario.
In the past, very few robust implementations for industrial applications that exploit HPC platforms have been developed. This is because the use of HPC approaches in electric-production simulation is a relatively new concept. Recent Department of Energy planning in grid-modernization research and development highlights the need for planning tools that support production simulation to assess and design electric grid systems that are more affordable, reliable, resilient, and that produce lower emissions. We believe that the research in this project has leveraged the Lawrence Livermore National Laboratory’s expertise and capabilities in HPC, and enabled the Laboratory to establish technical leadership nationally and internationally in smart-grid systems, and enabled programmatic growth in government and industry.
Scientific Approach and Accomplishments
In this project, we have developed new decomposition schemes to solve SMIPs. As mentioned before, SMIPs are a generalization of MIPs used to deal with optimization under uncertainty. Typically, stochastic optimization problems are formulated as multi-stage optimization problems where some model parameters are random variables (with known probability distributions). In each stage, a decision has to be made, and after each decision is made, one learns the realization of some of the random variables. Usually, the goal is to minimize the expected total cost, where the expectation is over all realizations. (For a detailed discussion, see Haneveld and van der Vlerk 1999.) In this project, we focus on two-stage SMIPs, a common variant in which the optimization problem is subdivided into two stages. For two-stage SMIPs, the first-stage variables determine the set of decisions before the uncertainty takes place. Second-stage variables represent the set of decisions to be taken once the uncertainty is revealed, as recourse to the decisions taken in the first stage. SMIPs are typically approximated via Sample Average Approximation (Kleywegt et al. 2002), thus transforming the problem into one large MIP, thus enabling the use of traditional MIP approaches.
We focused on two kinds of decomposition schemes to solve SMIPs: B&B decomposition schemes, and Scenario-Decomposition schemes. In the following section, each of these technical approaches and our results are described.
Research Thrust 1: Branch and Bound (B&B) Decomposition Schemes
General-purpose MIP solvers usually do not solve SMIPs efficiently because of the rapid growth in problem size as a function of the number of samples. The B&B algorithm is the most commonly used method for solving MIPs to optimality. It is a search algorithm that systematically partitions a problem into smaller subproblems and searches the solution space using a dynamically generated tree data structure called the B&B tree. In LP-relaxation-based B&B, the quality and promise of subproblems is evaluated by solving a linear programming (LP) relaxation formed by relaxing all integrality constraints. In contrast to previous approaches, we leverage the dual block-angular structure of SMIPs to solve LP relaxations using a parallel simplex method, significantly improving the scalability of B&B approaches for solving SMIPs. PIPS-S is a parallel implementation of primal and dual simplex that has been recently developed to solve LP problems with dual block-angular structure, such as the LP relaxation of the extensive formulation. We incorporate PIPS-S in our approach as the primary LP solver. The product (an output of this project) is a decomposition-based, distributed-memory B&B-based solver for SMIPS, called PIPS-SBB (PIPS: Simple B&B).
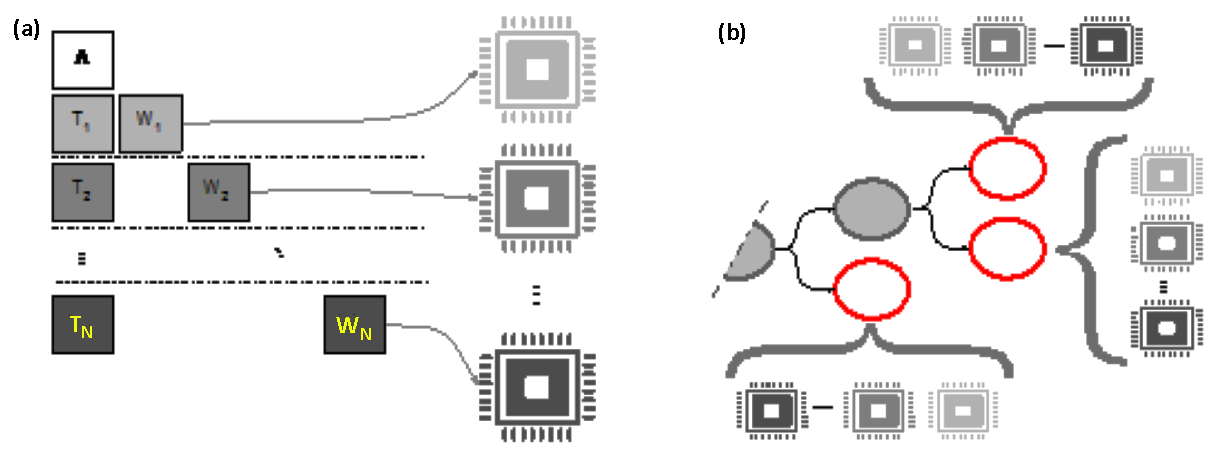
PIPS-SBB achieves speed-up by using PIPS-S as its LP solver to exploit data parallelism when processing each B&B node (see Figure 1). This architectural decision avoids scaling bottlenecks associated with parallel-node exploration. PIPS-SBB incorporates new methods for pre-processing, branching, node-selection, and heuristics that maintain the decomposable structure of SMIPs. These methods also apply to any MIP with dual block-angular structure; we focus on the SMIP case due to its prevalence in the literature and in applications.
The main contributions of PIPS-SBB, a novel B&B algorithm for general two-stage stochastic mixed-integer programs, are the following:
- PIPS-SBB is the first B&B algorithm to solve LP relaxations using a distributed-memory simplex algorithm that leverages the structure of SMIPs.
- By distributing SMIP data, PIPS-SBB can leverage the distributed-memory architecture of supercomputers to address more memory and optimize larger problems.
- After adapting methods known to accelerate MIP solvers to a distributed-memory setting with dual block-angular data structure, our initial results on benchmark Stochastic Integer Programming Library (SIPLIB) instances show the effectiveness of our method.
To further accelerate the performance of PIPS-SBB, we also incorporated two frameworks for parallelizing the B&B tree, and implemented them as extensions of PIPS-SBB. By parallelizing the B&B tree search in PIPS-SBB, we incorporate two levels of parallelism: (1) in the LP solver, and (2) in the B&B tree search. This additional level of parallelism added to PIPS-SBB with parallel-node exploration enables us to increase its scalability.
Both approaches leverage multi-level parallelism to scale efficiently beyond the natural limitations of each framework in isolation. The main contributions of this extension to PIPS-SBB are as follows:
- It provides a novel framework for fine-grained parallel B&B tree search for solving mixed-integer programs.
- Two new multi-level distributed-memory parallelisms for solving SMIPs are implemented as extensions of the distributed-memory SMIP solver PIPS-SBB
- PIPS-PSBB: B&B parallelism is implemented using the new fine-grained parallelism.
- ug[PIPS-SBB,MPI]: B&B parallelism is implemented using a ubiquity generator (ug). The coarse-grained parallel B&B framework is available as part of the SCIP optimization suit.
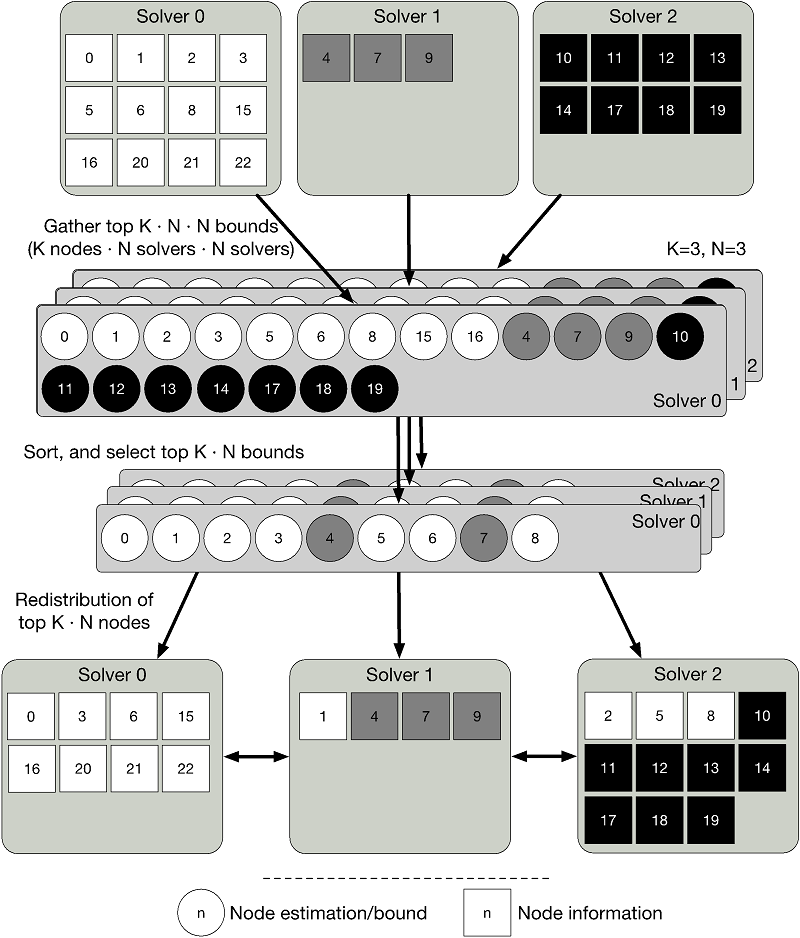
PIPS-PSBB is a decentralized fine-grained, yet lightweight parallel framework built as an extension to PIPS-SBB. We note that our approach and ideas are general and can be applied to any MIP solver. A primary aspect to consider in the design of parallel B&B algorithms is the policy used in the distribution of work, as well as the degree and frequency of communication used to coordinate parallel solvers. The objective of our new parallel B&B implementation is to increase parallel efficiency by minimizing the number of redundant nodes explored. We actively target this goal by ensuring that the set of active nodes being explored is always the most promising one. PIPS-PSBB uses a lightweight mechanism for redistributing the most promising nodes among all the parallel processors without the need for a centralized load coordinator. Instead of point-to-point communications, parallel processors exchange subproblems via all-to-all collective Message Passing Interface (MPI) asynchronous communications, enabling the framework to rebalance the computational load using a single communication step (see Figure 2).
Leveraging the parallelism in two levels (LP solvers and B&B tree search) simultaneously yields multiplicative effects on speedup and parallel scaling efficiency (in a weak or strong sense). In the specific case of B&B parallelizations for practical MIP instances, it is non-trivial to achieve even 20 percent strong-scaling efficiency beyond 100-1,000 processors (modest by HPC standards). By providing an extra level of parallelism, available processing power can be partitioned across multiple levels to improve overall efficiency and speedups over allocating the same number of processes to either single level of parallelism. We studied this phenomenon by analyzing parallel scaling on sslp_10_50_500, a Stochastic Server Location Problem (SSLP) instance from the SIPLIB. Given 500 cores (as many as the number of scenarios), the best configuration is to distribute the 500 available processors among 20-25 PIPS-SBB solvers, with each solver getting 20-25 processors. This result regarding multi-level parallelism is an important point to make, and further confirmed by other experiments: when large process counts are available, performance can be significantly improved by distributing them among different levels of parallelism.
Figure 2. Steps of the node-exchange process. Node estimates (circles) are gathered using all-to-all communication and sorted at each solver. When each solver has determined (in parallel) which nodes need to be exchanged, actual node information (squares) is redistributed using point-to-point communication.
Research Thrust 2: Scenario-Decomposition Schemes
Scenario-decomposition schemes typically relax the constraints that tie the scenarios together (non-anticipativity constraints). By doing so, the SMIP decomposes into a problem for each scenario. However, these single-scenario problems now result in different first-stage solutions for each scenario, requiring an iterative scheme that continues until first-stage solutions converge. Synchronous distributed-memory parallel implementations of scenario-decomposition schemes have been shown to perform well against SSLP instances from the SIPLIB, but do not work as well on others, such as stochastic supply chain (SSCh) instances.
In this project, we improve upon these prior implementations in three ways:
- We present new improvements to accelerate each iteration of scenario decomposition parallel algorithms.
- We develop an asynchronous, distributed implementation which incorporates these improvements, and show that it outperforms the synchronous implementation. In particular, the asynchronous version of the algorithm performs well and is able to solve one previously unsolved SSCh instance from SIPLIB.
- We develop optimal scenario grouping (OSG), a technique for grouping scenarios in such a way that it optimizes the bound improvement at each iteration, resulting in significant improvements to the performance of scenario-decomposition algorithms.
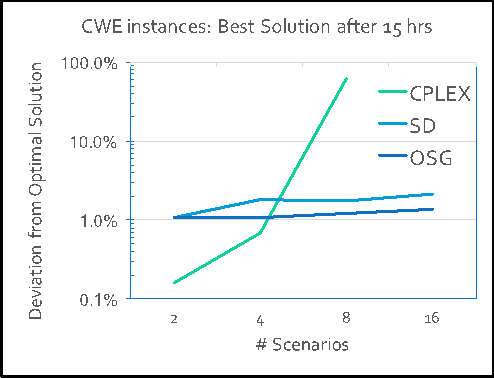
We present our results using real-world power-grid instances from Central-Western Europe. These instances are computationally difficult, and state-of-the-art MIP solvers are unable to find any feasible solutions for a high-resolution model of 16 scenarios (see Figure 3). On the other hand, scenario-decomposition schemes find a high-quality solution (less than 2 percent from optimal) after just one iteration. Applying techniques from OSG, we are able to improve the performance of scenario-decomposition (SD) schemes by more than 40 percent, finding solutions just 1 percent away from optimal.
Figure 3. Common weakness enumeration (CWE) instances. Optimal scenario grouping (OSG) improves scenario-decomposition (SD) schemes by 40 percent. General-purpose mixed-integer program solvers (CPLEX) are unable to solve the 16-scenario instance.
Impact on Mission
Power-grid modernization has emerged as a top priority in the grid-planning process, with planning modeling and simulation (and product-cost simulation) playing key roles. Decomposition methods such as those explored by our research are highly relevant to providing leap-ahead modeling and simulation capability in this area. By developing algorithms that leverage HPC resources, our research helps to broaden the base of HPC users working in new industrial sectors critical to U.S. economic and energy security, a core mission of the DOE. This research has also built expertise in power-grid optimization at the Laboratory, and has helped bring external recognition of the Laboratory’s expertise in solving stochastic optimization problems.
Conclusion
In this project, we developed novel decomposition-based algorithms for solving power-grid optimization problems with uncertainty. Many of the ideas in this research thrust have been developed in collaboration with academia, and this collaboration is expected to continue in other projects. Based on the results of this project's research, follow-on research projects, one sponsored by the DOE Advanced Grid Modeling program and another sponsored by the Office of Defense Nuclear Nonproliferation, are currently under consideration.
Publications and Presentations
Damci-Kurt, P., et al. 2016. “A Polyhedral Study of Production Ramping.” Mathematical Programming 158, Issue1-2: 175-205. doi:10.1007/s10107-015-0919-9. LLNL-JRNL-732987.
Munguía, L.-M., et al. 2016a. “PIPS-SBB: A Parallel Distributed-Memory Branch-and-Bound Algorithm for Stochastic Mixed-Integer Programs.” IPDPS Workshops: 730-739. doi:10.1109/IPDPSW.2016.159. LLNL-JRNL-678917.
——— 2016b. “PIPS-SBB: Implementation of Parallel Branch-and-Bound Algorithm for Stochastic (or Block-Angular) Mixed-Integer Programs.” Open-source code, https://github.com/LLNL/PIPS-SBB. LLNL-CODE-699387.
——— Forthcoming. “Parallel PIPS-SBB: Multi-Level Parallelism for Stochastic Mixed-Integer Programs.” LLNL-JRNL-739981.
Patsakis, G., et al. Forthcoming. “Optimal Black Start Allocation for Power System Restoration.” LLNL-JRNL-738940.
Ryan, K., et al. 2016. “Scenario Decomposition for 0-1 Stochastic Programs: Improvements and Asynchronous Implementation.” IPDPS Workshops: 722-729. LLNL-JRNL-678424.
——— Forthcoming. “Optimization Driven Scenario Bunching.” INFORMS Journal of Computing. LLNL-JRNL-681105.