Chuck Divin (17-ERD-021)
Abstract
Recent advances in energy-resolving x-ray detectors promise rich multispectral data with the simplicity of conventional gross-counting detector setups. However, effectively utilizing multispectral x-ray data will require novel approaches since extending current dual-energy algorithms leads to undesirable artifacts and poor material discrimination. We explored new multispectral decomposition and reconstruction algorithms based on realistic multispectral models. The new algorithms increase the accuracy of material measurements and reduce artifacts in x-ray computed tomography reconstruction.
Background and Research Objectives
Conventional x-ray computed tomography (CT) systems combine a broadband x-ray source with an array of current-integrating or charge-integrating x-ray detectors in a high-throughput configuration with high-spatial resolution. This combination has enabled x-ray CT to address numerous medical, industrial, and security applications (Martz et al. 2016). However, single-energy systems provide minimal information on elemental composition. State-of-the-art dual-energy instruments are able to provide some elemental composition by measuring the object transmission using two slightly different source spectra generated through filtering and varying the source potential (Azevedo et al. 2016). The effectiveness of dual-energy CT (DECT) is limited by two factors. First, DECT attempts to transform x-ray attenuation measurements into a different basis using inaccurate models of the physics of x-ray attenuation. Second, the measured spectra are inefficient in discriminating the physical basis functions due to poor energy separation; much of the spectra are either too strongly or too weakly absorbed. Also, current decomposition methods poorly account for high-Z elements, which impose strong absorption edges on the transmitted x-ray spectrum.
Recent advances in cadmium telluride (CdTe) and cadmium zinc telluride (CZT) pixelated energy-resolving detectors have enhanced the capabilities of Multi-Spectral X-ray Computed Tomography (MSXCT) in which the energy of each deposited x-ray is recorded. Theoretical studies examining detectors with ideal energy resolution have indicated that MSXCT outperforms conventional charge-integrating computed tomography in image quality and detection specificity (Wang et al. 2011; Ding and Molloi 2012). Multiple energy bins can be generated in a single data acquisition with minimal overlap in the x-ray spectrum. This promises improved material identification and the ability to correctly account for absorption edges.
The objective of this project was to evaluate how multispectral 3D x-ray data can be transformed into a parameter space that enables better material identification and discrimination. The mathematical transform process is called decomposition and requires the operator to choose a set of basis functions that define the transformation. The objective of this project was to determine the set of basis functions and material physics that yield optimal detection performance relevant to Lawrence Livermore National Laboratory's programs, and minimize creation of undesirable artifacts in the decomposition and reconstruction process.
Scientific Approach and Accomplishments
We investigated two decomposition methods for this project. The first method extended an existing state-of-the-art dual- energy decomposition by including additional attenuation mechanisms such as coherent scattering that are ignored in conventional material approximations. The second method addressed the quantization of noise that arises in flux-limited multispectral data.
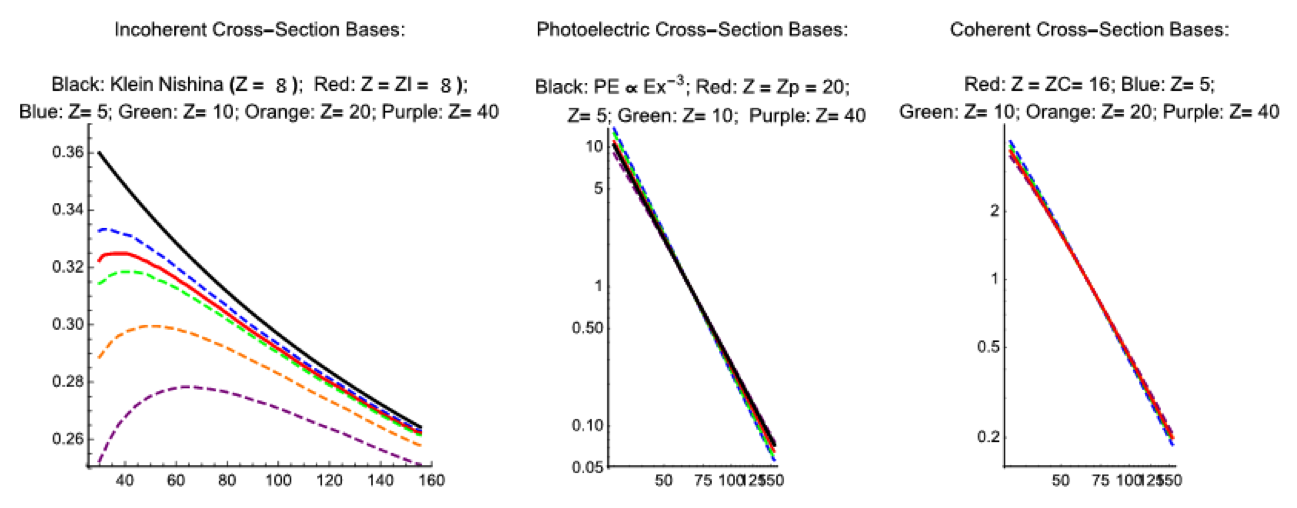
Conventional DECT uses transmission measurements from two broad-band spectra (one with a higher average energy, the other with a lower average energy; Azevedo et al. 2016). The decomposition process maps the x-ray absorption onto two bases: (1) the Klein-Nishina scattering basis that models the incoherent Compton scattering for a free electron, and (2) a power-law E-3 approximation of photoelectric absorption. These bases provide an approximation of the energy-dependent attenuation mechanisms shown Figure 1.
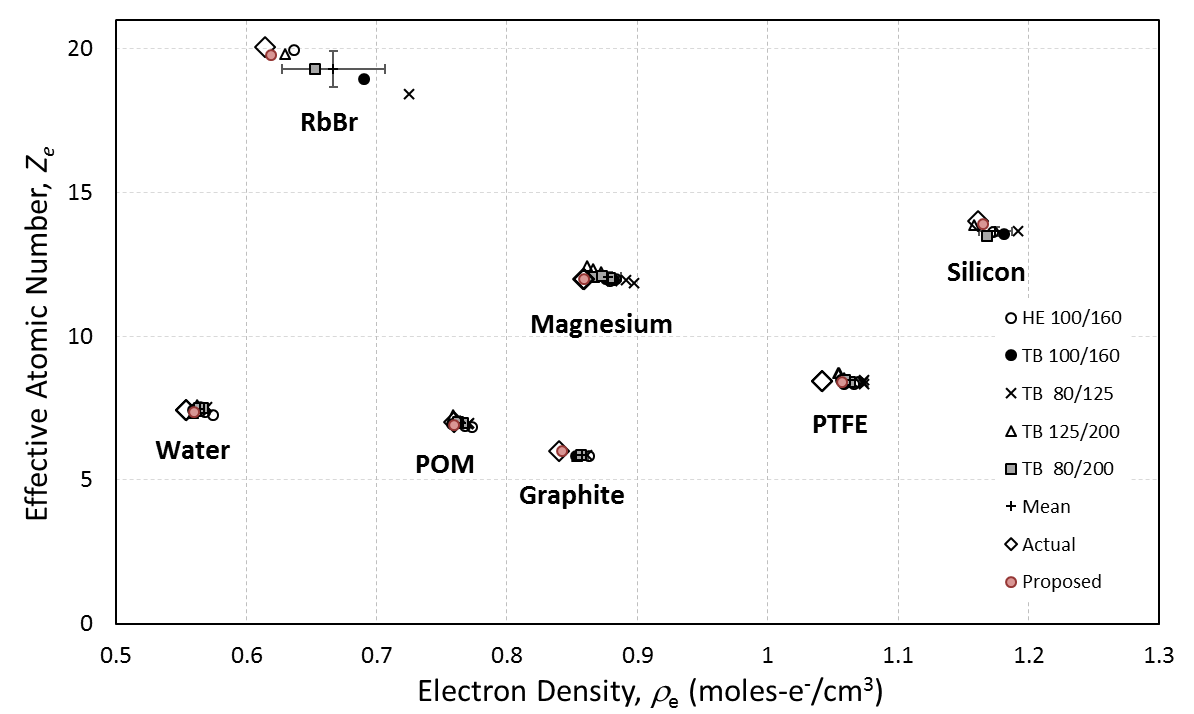
The Kline-Nishina and photoelectric approximations are then cast into second parameter space (ρe, Ze) via calibrated polynomial expressions, where ρe and Ze are the average electron density and effective atomic number, respectively. The Laboratory's implementation of this technique (known as SIRZ) has been highly successful over a limited dynamic range in material properties. The limits on this range are largely due to inaccuracies in the basis-function description, and from the limited (and overlapping) information provided by the broadband spectra.
A series of parameterized basis functions, (ZI, ZP, ZC), were created to more accurately model the incoherent, photoelectric, and coherent scattering. As shown in Figure 1, the functions smoothly predict the scattering strength as a function of incident x-ray energy and atomic number, Z. In particular, the incoherent Compton model (ZI, solid red) is indistinguishable from the measured cross-section (dashed red) at Z = 8, while the conventional Kline-Nishina approximation shows significant deviation at energies greater than 50 keV.
The increased accuracy of the new decomposition bases is shown in Figure 2, which is adapted from SIRZ. In the previous work, x-ray computed tomography scans of seven materials were acquired on multiple systems. The dual energy scans were decomposed into a (ρe, Ze) parameter space using the incoherent and photoelectric approximations. This process works well for a limited range of elemental composition range of Z = 6 to Z = 14. The proposed "ZI, ZP, ZC" (IPC) decomposition extends the range of accurate decomposition to materials with a range of Z = 4 to Z = 26.
The second multispectral algorithm investigated by this project addressed the quantization challenge that arises in scenarios where time or safety considerations limit the total dose available for scanning. In these scenarios, the small number of detected x-rays on each pixel or energy bin degrades the CT reconstruction with increased noise, streaking, and other artifacts. While numerous solutions exist for conventional single energy CT reconstruction with limited photon statistics, they are not compatible with the decompose-then-reconstruct approach used in MSXCT, since the decomposition transform does not preserve the incident photon statistics (Poisson or Gaussian approximation).
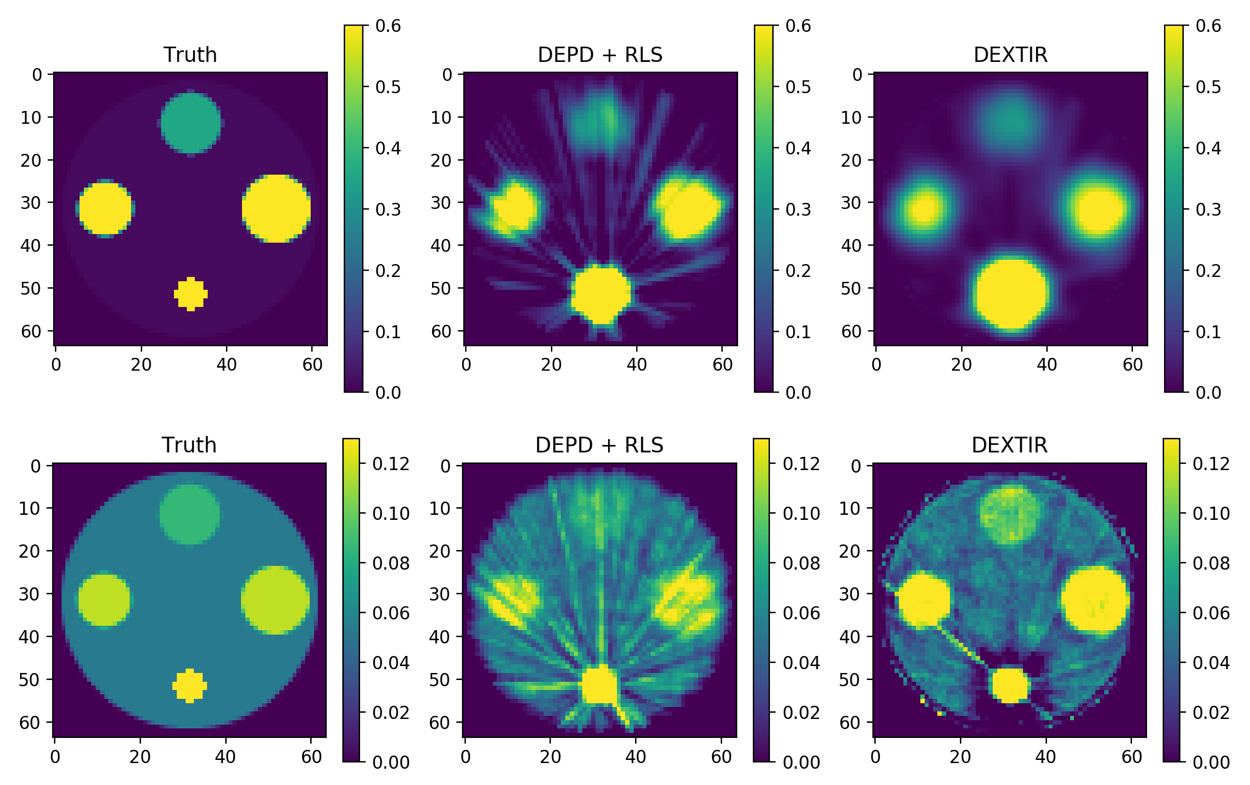
The Dual-Energy X-ray Tomographic Iterative Reconstruction (DEXTIR) technique solves the problem of propagating noise models in the conventional two-stage approach by placing both steps in a single iterative loop. This approach uses a gradient-descent algorithm to decompose and reconstruct MSXCT data base while imposing quadratic regularization (i.e., regularized least squares, RLS), accurate positivity constraints, and realistic noise models. The realistic noise models are included via a per-detector-view weighting that deemphasizes regions within a projection that have high relative noise (i.e., are photon-starved). The results of the decomposition are shown in Figure 3. All the above features of the multi-spectral decomposition (MSD) algorithm result in lower noise in the reconstructions. In addition, if the MSD algorithm is stopped early, it results in regularization of the reconstruction and reduces overfitting.
Impact on Mission
The proposed decomposition algorithms highlight several ways that multispectral x-ray CT can extend the capabilities of conventional x-ray radiography and computed tomography. Programs that need to image complex assemblies made from diverse materials (Stockpile Stewardship) or differentiate between similar materials (Global Security / Livermore's Explosive Detection Program) will benefit from more accurate measurements images with fewer artifacts and noise. This project further enhances the Laboratory's core competency in non-destructive evaluation and maintains our position at the forefront of x-ray computed-tomography development.
Conclusion
This project demonstrated that two new multispectral decomposition and reconstruction algorithms increase the accuracy of material measurements and reduce artifacts in x-ray computed tomography reconstructions. The new algorithms stand to enhance Livermore's capabilities in stockpile stewardship, especially in non-destructive evaluation of complex assemblies and explosives.
References
Azevedo, S. G., et al. 2016. "System-Independent Characterization of Materials Using Dual-Energy Computed Tomography." IEEE Transactions on Nuclear Science 63 (1):341—350. doi: 10.1109/TNS.2016.2514364.
Ding, H., and S. Molloi. 2012. "Image-Based Spectral Distortion Correction for Photon-Counting X-ray Detectors." Medical Physics 39 (4): 1864—1876. doi: 10.1118/1.3693056.
Martz, H.E., et al. 2016. "X-Ray Imaging: Fundamentals, Industrial Techniques and Applications." CRC Press.
Wang, A. S., et al. 2011. "Pulse Pileup Statistics for Energy Discriminating Photon Counting X-ray Detectors." Medical Physics 38 (7): 4265—4275. doi: 10.1118/1.3592932.