Sebastien Hamel (16-ERD-011)
Project Description
At Lawrence Livermore, many applications require equation-of-state models that must span up to nine orders of magnitude in both density and temperature. Consequently, we need tools that are both accurate and efficient throughout the entire phase and across diverse physical regimes, including materials under expansion, condensed matter, warm dense matter, and plasmas. Most of these phases are completely inaccessible to focused science experiments, meaning we must rely heavily on theoretical methods. Our current theoretical workhorse for making highly accurate predictions of equation of state is the quantum molecular dynamics method based on density functional theory (used to investigate the electronic structure of many-body systems). While this method has proven highly successful in describing the properties of many materials from first principles, it is typically limited to temperatures below about 5 to 10 eV because of a steep increase in computational cost with increasing temperatures. Alternative methods that are efficient at high temperature become increasingly difficult to use as the temperature falls. A fundamentally different formulation of the equations for density functional theory is needed to enable high-energy-density science at temperatures two to three orders of magnitude higher (1–10 keV) than is currently feasible. Earlier work strongly suggests that quantum molecular dynamics methods based on density functional theory will be accurate at ultrahigh temperatures and pressures, if the computational challenges can be overcome. We are developing such a method to provide accurate and efficient quantum simulations of material properties across an extreme range of densities, pressures, and temperatures. Our spectral quadrature method formulates density functional theory densities, energies, and forces as spectral integrals, yielding a linearly scaling method that is well suited to massively parallel computer architectures and applicable to metals and insulators. We will use the resultant code to determine melt lines as well as shock and release states in the multiple-megabar regime for different categories of materials.
For this project, we expect to deliver standard quantum molecular-dynamics capabilities, which will include various ensembles and access to structural and transport properties, in a highly scalable implementation. Results will also include calculations over a wide variety of densities and temperatures (up to 1 keV) of the equations of state of different classes of materials with very different electronic band gaps and metallization properties, including molecular compounds and covalent extended, ionic, and metallic systems. In addition, we will determine the melting line and high-temperature behavior of different classes of materials such as iron, water, magnesium oxide, and enstatite, a common rock-forming mineral, at multiple-megabar pressures. If time permits, we also will use this new capability to establish the mass–radius relationships for super-Earth exoplanets. This work will address a crucial gap in our current theoretical capabilities that is limiting our ability to fully leverage exciting, new, high-energy-density experimental facilities such as the Linac Coherent Light Source at the SLAC National Accelerator Laboratory at Stanford and Lawrence Livermore's National Ignition Facility.
Mission Relevance
The capabilities we intend to develop will form a critical part of the theoretical and computational infrastructure of LLNL, enable high-energy-density science in the warm dense matter regime, and will provide a completely new capability at ultrahigh temperatures for addressing new science. Thus, this project will enhance the Laboratory's high-energy-density science core competency and support the strategic focus area of stockpile stewardship science.
FY16 Accomplishments and Results
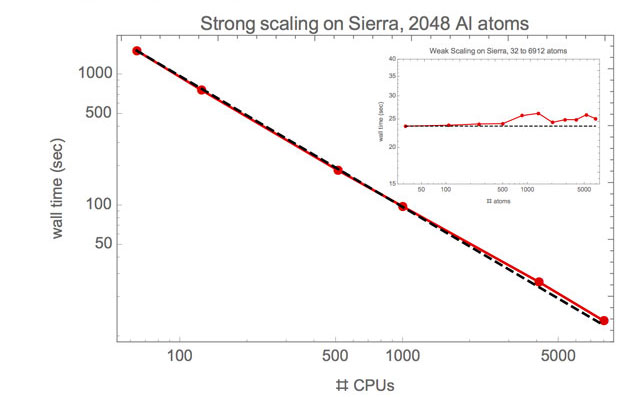
In FY16 we (1) verified convergence of the energy and atomic forces of the developed spectral quadrature formulation and implementation to the plane-wave result; (2) determined that the energy and atomic forces converge systematically to the plane-wave result—in particular, the method was demonstrated to achieve extremely high accuracy in both energy and forces for both insulating and metallic systems, thereby overcoming one of the important limitations of previously developed approaches; (3) studied the strong and weak scaling of the developed formulation and implementation of spectral quadrature and found that it demonstrates extremely good scaling (see figure); and (4) generated pseudopotentials, which are used as approximations for the simplified description of complex systems, and tested them for systems of interest.