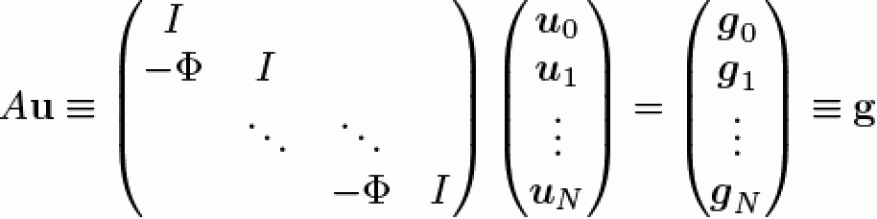Jacob B. Schroder (14-ERD-013)
Abstract
The need for parallel-in-time methods is being driven by the rapid changes in computer architectures, where future speedups will come from greater concurrency, not faster clock speeds, which are stagnant. These changes are giving rise to the sequential time-integration bottleneck. The goal of this project was to develop an algorithm well-suited for exascale computing that exposes parallelism in time and computes multiple time steps simultaneously in parallel. The resulting algorithm accelerates time-stepping methods and avoids the sequential bottleneck. The approach is based on a nonintrusive multigrid reduction-in-time method (MGRIT), where a multilevel structure leverages successively coarser time-scales to accelerate the solution on the original finest time scale. Overall, the algorithm exposes parallelism in the temporal dimension while iteratively converging to the global space-time solution. The project focused on (1) linear and nonlinear parabolic problems, showing excellent convergence properties and speedups; (2) hyperbolic problems, where a two-grid convergence theory was developed and applied to model hyperbolic problems; and (3) applying MGRIT to Burger's equation, which showed the introduction of a shock did not significantly degrade performance. In conclusion, the outlook for parallel-in-time methods is strong because the future increases in concurrency require such new sources of parallelism. This work has laid the groundwork to address this challenge and use parallel-in-time methods with our codes.
Background and Research Objectives
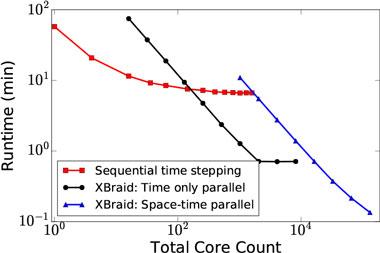
Growth in high-performance computing will come from more central processing unit cores, not faster clock speeds. Previously, faster clock speeds decreased the compute time per time step, and thus allowed for more time steps without increasing the overall compute time. However, clock speeds are no longer increasing, which will inevitably lead to increases in compute time. The rapidly changing nature of computer architectures, where future speedups will be available through greater concurrency, are giving rise to the sequential time integration bottleneck, visible when the strong scaling limit in space is reached and sequential time-stepping flatlines (Figure 1). The bottleneck can only be avoided by exploiting parallelism in the time dimension. Our goal was to convert time-stepping to a process that is well-suited for exascale computing, where multiple time-intervals are computed concurrently, resulting in a large speedup and a solution to the time-integration bottleneck.
The parallel-in-time approach we developed is MGRIT, which is implemented in the XBraid parallel-in-time software package, also a product of this project.1,2 XBraid is a scalable, optimal, general, and non-intrusive time-parallel approach (see Figure 1). Time-parallel work dates to at least 1964 and includes recent and important additions, including the time-discretization specific work on PFASST, the parallel full approximation scheme in space and time algorithm, which is a method for parallelizing ordinary and parallel differential equations in time.3–6 XBraid is equivalent in a two-grid setting to Parareal, a parallel-in-time integration method, but generalizes the method to a scalable and optimal multilevel setting. Compared to PFASST, MGRIT is time-discretization agnostic and is designed to interface with arbitrary user-codes.
Our objectives were to develop a publicly available and general-purpose parallel-in-time code. Over the project's three years, we validated MGRIT for basic parabolic problems, compared three different multigrid-in-time strategies, studied how to run MGRIT efficiently for nonlinear problems, and established MGRIT theory for model parabolic and hyperbolic problems.1,7–9 We also provided regular updates to XBraid, which was released under Lesser General Public License (LGPL) 2.1 and had more than 150 tracked downloads. We also conducted numerous fruitful collaborations with colleagues from Monash University in Melbourne, Australia; Memorial University of Newfoundland in Canada; University of Colorado in Boulder, Colorado; University of Cologne in Germany; University of Stuttgart in Germany; and the U.S. Department of Defense.1,7,8,10–13
Scientific Approach and Accomplishments
Our overall approach is based on the nonintrusive MGRIT method (as implemented in XBraid), where a multilevel approach leverages successively coarser timescales to accelerate the solution on the original finest timescale. The result is an iterative algorithm that exposes parallelism in the temporal dimension and that converges to the same global space–time solution as sequential time-stepping.
XBraid adds time-parallelism to existing codes by parallelizing the solution to the global bidiagonal space–time system induced by sequential time-stepping (see Equation 1).
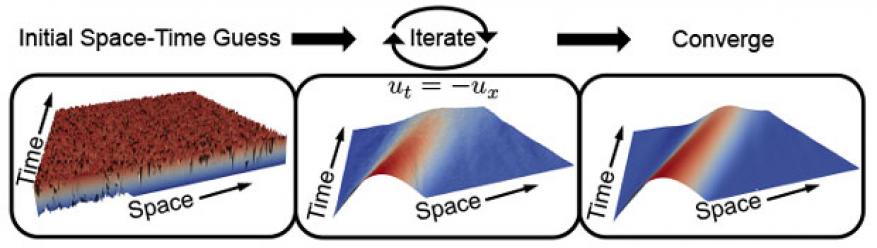
Traditional time-stepping solves this system sequentially with forward-substitution. XBraid, however, non-intrusively wraps the existing user time-stepping routine, ϕ, and solves Equation 1 iteratively with an optimal multigrid reduction method, adding massive new concurrency. The new parallelism is achieved with a hierarchy of ever coarser time grids (i.e., with larger time-step size) that accelerate the solution on the finest time grid (see Figure 2). The nonintrusiveness is achieved with a conceptually simple interface, which allows the user to wrap their existing time-stepping routine to define the ϕ operator.
Our initial focus was on parabolic problems, first linear and then nonlinear. We started by detailing the basic facets of XBraid and introduced the nonintrusiveness, multilevel optimality, and FCF-relaxation (which can be thought of as line relaxation in space).1 FCF-relaxation is a key difference with XBraid, and is a more robust alternative to the F-relaxation present in Parareal. Essentially, FCF-relaxation is more effective than F-relaxation because it is better at damping the spatially oscillatory error, leaving the smoother error for reduction on the coarse time grids. This more powerful relaxation is what allows XBraid to exhibit scalable iteration counts in a multilevel setting. To run nonlinear parabolic problems efficiently in this setting, certain changes were needed.8 The key difficulty was that solving the nonlinear time-step equation became progressively more difficult on coarser time grids, resulting in a loss of efficiency. To mitigate this increasing time-step cost on coarse time grids, we pursued strategies such as simultaneous space–time coarsening to control the conditioning of the nonlinear time-step system and level-dependent tolerances for each nonlinear time-step evaluation. Lastly, the parallel studies for the linear and nonlinear cases validated XBraid as an algorithm that scales well in both a strong and weak sense.
Our next focus was on hyperbolic problems, which are programmatically important to Lawrence Livermore. A key development here was the two-grid convergence theory we developed.9 We discovered that spatial discretizations that yield purely imaginary eigenvalues are not well-suited for the current XBraid. While there are research avenues to improve performance in this setting, we uncovered a simple path forward: artificial dissipation. A small, grid-dependent amount of artificial dissipation can allow for good XBraid performance on model advection problems, including Burger's equation with shocks. Regarding Burger's equation, the presence of a shock did not significantly degrade performance.
The focus on hyperbolic problems also forced our group to research the use of explicit time-stepping schemes. Here, spatial coarsening must be coupled with temporal coarsening for stability on coarse temporal grids. However, we discovered that spatial coarsening in regions where the solution is near zero is detrimental to MGRIT performance, given that the space–time problem becomes anisotropic in these regions. This anisotropic behavior occurs because there is no coupling in the spatial direction in the underlying equation. Thus, spatial coarsening leads to an irrevocable loss of information and related degradation in XBraid convergence. The solution was to adaptively coarsen in space, but only in those regions where the stability limit would be violated on the coarse time grid. We continue to work with our Monash University collaborators to complete this work on Burger's equation. The result will be, as far as we know, the first scalable parallel-in-time solution to Burger's equation.
We also addressed two additional focus areas. In the first area, we compared the three basic approaches to multigrid in time, coarsening only in space, in time, and full space–time.7 This work produced the first parallel implementations of some of the above algorithms and considered first- and second-order time-stepping schemes. Not surprisingly, full space–time coarsening (supported by XBraid) is the most efficient, but coarsening only in time (the default XBraid setting) is the least intrusive. The other focus area involved an examination of moving meshes.10 Here, we demonstrated, for the first time, XBraid optimality for a moving mesh problem. Work on full space–time adaptive meshing continues with Ben O'Neill of the University of Colorado, as a part of his dissertation work.
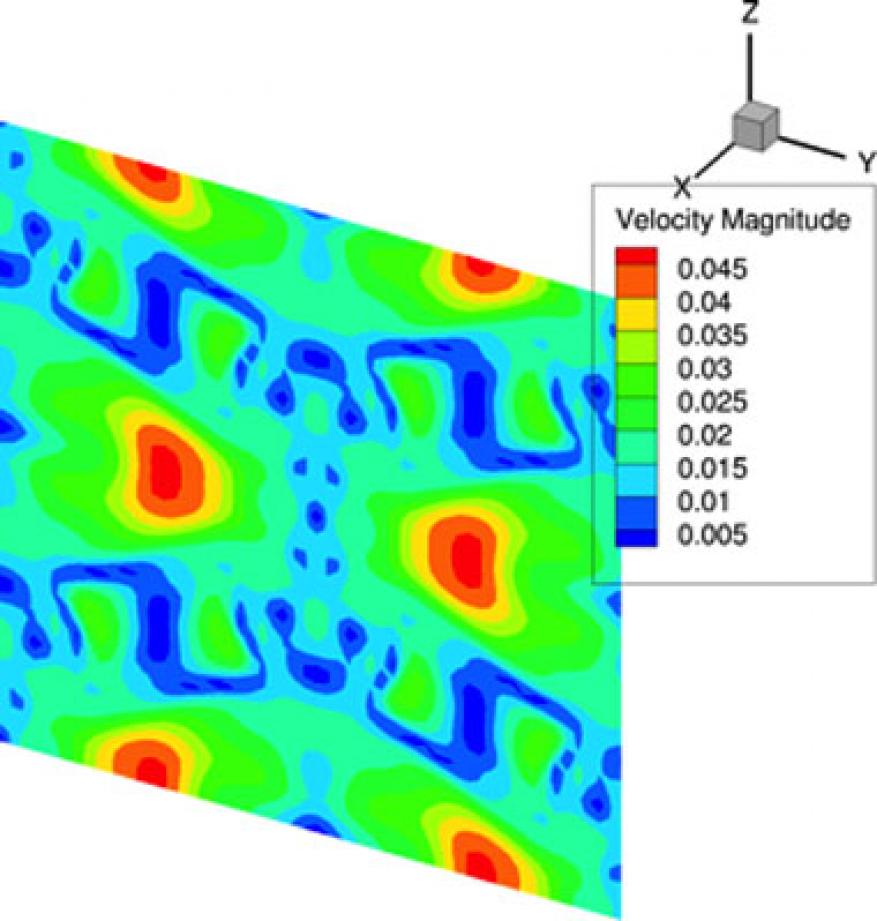
Our group has also leveraged the groundwork laid in this effort. Separate projects have used XBraid for a variety of problems, including a two-dimensional unsteady flow vortex-shedding example, a three-dimensional Taylor-Green example (see Figure 3), and various power-grid systems.12,13
Impact on Mission
Our algorithm to expose new parallelism in the time dimension allows Laboratory codes to run faster and to better take advantage of the huge increase in concurrency coming with exascale computing. Our algorithm supports the high-performance computing, simulation, and data science core competency, along with several LLNL mission areas that depend on these computing resources. Essentially, all Livermore production multiphysics codes make use of explicit time stepping, and are therefore subject to the serial time-integration bottleneck. The need for parallel time integration is imminent, and developing this technology and associated expertise helps the Laboratory maintain its leadership in high-performance computing ecosystems.
Conclusion
The outlook for parallel-in-time methods is strong because the coming increases in concurrency require us to find new sources of parallelism. The sequential time-integration bottleneck is real and unavoidable. The goal of this work was to allow Laboratory codes to run faster, avoid the sequential time-integration bottleneck, and better take advantage of exascale level concurrency. Our results laid the required groundwork for using parallel-in-time methods and put the Laboratory at the forefront of this rapidly growing field.
The next step is to identify important application areas for XBraid. Interest has been expressed from the neutron transport and BLAST shock hydrodynamics teams. Our group will also pursue outside funding, including, but not limited to, the Department of Defense, General Electric, and Proctor and Gamble, all of which have expressed interest in this work. The fundamental basic research and software infrastructure developed in our project has already led to funding from the Department of Energy for power-grid simulations and from the Department of Defense in two previous fiscal years for fluid dynamics simulations.
References
- Falgout, R. D., et al., "Parallel time integration with multigrid." SIAM J. Sci. Comput. 36(6), C635 (2014). LLNL-JRNL-645325. http://dx.doi.org/10.1137/130944230
- "XBraid: Parallel multigrid in time." Computation. (2017). LLNL-WEB-606892. http://llnl.gov/casc/xbraid
- Nievergelt, J., "Parallel methods for integrating ordinary differential equations." Comm. ACM 7(12), 731 (1964).
- Lions, J. L., Y. Maday, and G. Turinici, "A 'parareal' in time discretization of PDE's." C. R. Acad. Sci. Paris Ser. I. 332, 661 (2001).
- Minion, M. L., and S. A. Williams, Parareal and spectral deferred correction. AIP Conf. Proc. 1048, 388 (2008).
- Minion, M. L., "A hybrid parareal spectral deferred corrections method." Comm. App. Math. and Comp. Sci. 5, 265 (2010).
- Falgout, R. D., et al., Multigrid methods with space-time concurrency. (2015). LLNL-JRNL-678572.
- Falgout, R. D., et al., Multigrid reduction in time for nonlinear parabolic problems. (2016). LLNL-JRNL-692258.
- Dobrev, V., et al., Two-level convergence theory for parallel-in-time multigrid. (2016). LLNL-JRNL-692418.
- Falgout, R. D., et al., Parallel-in-time for moving meshes. (2016). LLNL-TR-681918.
- Gahvari, H., et al., A performance model for allocating the parallelism in a multigrid-in-time solver. 7th Intl. Workshop in Performance Modeling, Benchmarking and Simulation of High Performance Computer Systems, Salt Lake City, UT, Nov. 13, 2016. LLNL-CONF-701995.
- Lecouvez, M., et al., A parallel multigrid reduction in time method for power systems. Power & Energy Society General Mtg., Boston, MA, July 17–21, 2016. LLNL-CONF-679148.
- Falgout, R. D., et al., Parallel time integration with multigrid reduction for a compressible fluid dynamics application. (2014). LLNL-JRNL-663416.
Publications and Presentations
- Dobrev, V., et al., Two-level convergence theory for parallel-in-time multigrid. (2016). LLNL-JRNL-692418.
- Falgout, R. D., Multigrid methods with space-time concurrency. (2015). LLNL-JRNL-678572.
- Falgout, R. D., et al., Multigrid reduction in time for nonlinear parabolic problems. (2016). LLNL-JRNL-692258.
- Falgout, R. D., et al., "Parallel time integration with multigrid." SIAM J. Sci. Comput. 36(6), C635 (2014). LLNL-JRNL-645325. http://dx.doi.org/10.1137/130944230