Jeffrey Florando (17-ERD-029)
Executive Summary
We are developing a statistical methodology to demonstrate how to use uncertainty quantification to optimize the experimental and performance design of advanced materials, develop more robust material models, and advance the materials-qualification process. Understanding the fidelity and uncertainty associated with material models is integral to DOE/NNSA goals in maintaining the nation's nuclear deterrent without nuclear testing.
Project Description
With the development of new manufacturing processes that create materials with potentially very different pedigrees, there is a need to understand and quantify the influence of microstructural variability and other sources of statistical uncertainties on materials performance. The understanding of uncertainty is a key component to the path for material qualification. The traditional approach to qualifying a material involves an understanding of the properties that are tied to a performance metric. A series of experiments are being conducted to assess those properties under relevant conditions, and those results reduce the uncertainty to a level deemed acceptable. There are many applications, however, where the performance metric lies outside of the conditions accessible to focused experimental methods, and material models are needed to extrapolate to regimes of interest. The goal of our work is to develop a general statistical framework to understand and assess the uncertainties and variability associated with materials-strength modeling in the context of a performance problem, including those involving material produced using advanced processing methods. The Bayesian inference methodology, which is a statistical method that updates the probability of a hypothesis as additional information becomes available, has been applied to a number of material-science problems, including the prediction of fatigue lifetimes in metals, material models that predict the forces in a weld, and equation-of-state models in hydrodynamic simulations. There has also been work that outlines a more top-down approach to applying uncertainty quantification to the optimization of a material's performance. We will use Bayesian statistical methods in conjunction with a wide range of experimental data to evaluate several material constitutive models and determine how uncertainties are propagated to the performance problem of the jet velocity from a shaped-charge liner.
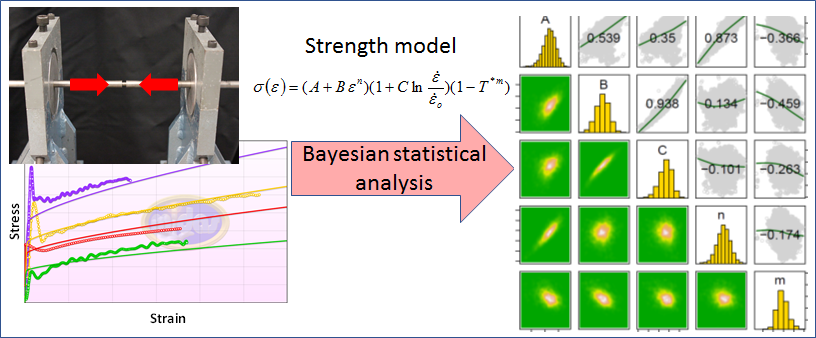
Utilizing strength data in the form of well-defined stress–strain curves, along with material-strength models, we expect to create model joint-parameter distributions (posterior distributions) that provide information about the degree to which models capture experimental data. These distributions will be propagated and compared to more integrated experiments where the stress–strain state is less defined. These experiments are closer to the regime of interest and sensitive to the strength of the material. The distributions will be propagated to understand the uncertainties associated with the performance. As part of the refinement process, statistical sampling methodologies and simulations will be used to guide where additional experiments can be performed to reduce the uncertainty. We will develop statistical tools to further refine the parameter distributions and bound the uncertainty. If successful, the outcome will be a statistical framework that demonstrates how uncertainty quantification can be used to optimize the experimental and performance design, develop more robust material models, and advance the materials-qualification process. This framework can then be applied to other performance problems to guide the allocation of additional experimental resources, increase confidence in the material models and their parameters, and aid in the material-qualification process.
Mission Relevance
Our research is at the intersection of Lawrence Livermore National Laboratory's core competencies in advanced materials and manufacturing and high-performance computing, simulation, and data science. With the advent of science-based stockpile stewardship, understanding the fidelity and uncertainty associated with material models is integral to this core mission, and is relevant to the DOE goal of maintaining the safety, security, and effectiveness of the nation’s nuclear deterrent without nuclear testing. We intend to provide a statistical framework that can be applied to materials-strength modeling to help understand the overall uncertainty as it pertains to a performance metric. In addition, the framework can be used to help guide where additional experimental resources should be applied to reduce that uncertainty.
FY17 Accomplishments and Results
In FY17 we (1) collected a set of stress–strain data on a well-characterized tantalum material; (2) applied the Bayesian statistical methodology with a Johnson–Cook strength model to the stress–strain dataset to create posterior distribution of the parameters; (3) applied a mixed-effects statistical model to the tantalum data to improve upon the accuracy of the predictive capabilities of the methodology; (4) evaluated model selection by conducting sensitivity studies on the parameters from strength models; and (5) evaluated methods to apply the Bayesian analysis to include data from higher-strain-rate experiments.
Publications and Presentations
Bernstein, J., et al. 2017. "Mixed Effects Material Strength Models with Model Discrepancy." Joint Statistical Meeting 2017. LLNL-ABS-718657.
Rivera, D., et al. 2017. "TMS Conference Abstract: Uncertainty Quantification in Materials Strength Models Using Bayesian Inference." LLNL-ABS-734322.
Schmidt, K., et al. 2017a. "Sensitivity Analysis of Strength Models Using Bayesian Adaptive Splines." 20th Biennial APS Conference on Shock Compression of Condensed Matter. LLNL-PROC-737638.
——— 2017b. "Sensitivity Analysis of strength models using Bayesian Adaptive Splines". 20th Biennial Conference of the APS Topical Group on Shock Compression of Condensed Matter. LLNL-ABS-725240.