A primary goal of LDRD is to foster excellence in science and technology that will, among other things, attract and retain the most qualified scientists and engineers and allow scientific and technical staff to enhance their skills and expertise.
Laboratory LDRD principal investigators and research teams receive numerous prestigious honors, awards, and recognition for LDRD-funded work. These recent honors attest to the exceptional capabilities, talents, and performances of these researchers, while simultaneously highlighting the success and vitality of the LDRD Program at Livermore.
American Association for the Advancement of Science Fellow
Livermore scientist Kenneth Turteltaub has been named a fellow of the American Association for the Advancement of Science. He was specifically noted for the development of ultra-precise accelerator mass spectrometry methods for biomedicine and work on carcinogenesis, the formation of macromolecules, and low-dose pharmacokinetics, or how pharmaceuticals move through the body. Turteltaub specializes in toxicology and metabolism of drugs and toxicants, accelerating development of new therapeutics, molecular mechanisms of disease, and biomedical applications of accelerator mass spectrometry. He received his bachelor’s degree in agriculture and his master’s degree in animal science from Ohio State University and his Ph.D. in toxicology from Iowa State University. He has participated in numerous LDRD projects dating back to 1988, including studies of accelerator mass spectrometry for biomedical use, protein structural analysis, carcinogen interactions with DNA, biomedical and environmental isotope tracing, toxicology and carcinogenesis research, and detection and countermeasures for global biosecurity. He was most recently a co-investigator for a project examining “Targeted Drug Delivery for Treating Traumatic Bone Injury” (11-ER-060). This year, 347 members have been named fellows because of their scientifically or socially distinguished efforts to advance science or its applications. The tradition of American Association for the Advancement of Science fellows began in 1874.
American Physical Society Fellows
All of the seven Lawrence Livermore scientists selected as 2015 fellows of the American Physical Society have served as investigators or co-investigators for LDRD projects. The new fellows represent a wide selection of physics expertise, ranging from laser–plasma interaction to optical techniques to computational condensed matter. Fellowships are awarded after extensive review and are considered a distinct honor because the evaluation process, conducted by the fellowship committees of individual divisions and topical groups and forums, relies on nomination and recommendation by one's professional peers.
- Lee Bernstein, an LDRD researcher since 1998, was cited by the Division of Nuclear Physics for “work developing novel methods of determining neutron–nucleus cross sections via high-resolution gamma-ray spectroscopy, the early development of surrogate ratio method and the study of nuclear processes in high energy density plasmas at NIF.” He is currently the principal investigator for project 14-ERD-034, “Nuclear Fission in a Plasma.” He is also a collaborator for projects 13-ERD-036, “Radiochemical Measurements of Nuclear Reactions at the National Ignition Facility” and 13-LW-003, “Why Is Nuclear Matter So Red?”
- Stavros Demos, an LDRD researcher since 1997, was cited by the Division of Atomic, Molecular and Optical Physics for “outstanding contributions using unique optical techniques to understand the relaxation dynamics of point defects and developing non-invasive biomedical photonics for rapid tissue assessment.” He is currently a co-investigator for project 14-ERD-098, “Laser–Matter Coupling Mechanisms Under Varying Chemical and Particulate Surface Configurations.”
- Pierre Michel, an LDRD researcher in 2008, was cited by the Division of Plasma Physics for “outstanding contributions to laser–plasma interaction physics and dynamic multiple-laser beam physics, enabling symmetry control in indirectly driven Inertial Confinement Fusion implosions.” He was co-investigator for project 08-LW-070, “Plasma Waveguide for Electron Acceleration.”
- Yuan Ping, an LDRD researcher since 2004, was cited by the Division of Plasma Physics for “pioneering experiments exploring the nature, equilibration and use of nonequilibrium plasmas strongly driven by coherent and incoherent sources.” She is currently a co-investigator for project 14-SI-003, “Physical States and Processes in Inertial Confinement Fusion: Matter at Extreme Energy Density.”
- Vladimir Smalyuk, an LDRD researcher since 2011, was cited by the Division of Plasma Physics for “seminal contributions to the understanding of hydrodynamic instabilities in Inertial Confinement Fusion using elegant experiments on OMEGA and NIF.” He is currently a co-investigator for project 14-ERD-028, “The Application of Imposed Magnetic Fields to Ignition and Thermonuclear Burn at the National Ignition Facility.”
- Fred Streitz, an LDRD researcher since 2002, was cited by the Division of Computational Physics for “important contributions to computational condensed matter physics and for leadership in extreme scale computation.” He last served as a co-investigator for project 10-ERD-004, “Mix at the Atomic Scale.”
- Damian Swift, an LDRD researcher since 2008, was cited by the Topical Group on Shock Compression of Condensed Matter for “wide-ranging contributions to shock- and ramp-wave compression experiments using laser, pulsed-power and explosive drivers, and for employing rigorous quantum and statistical mechanical principles to guide the formulation of theoretical solutions to experimental problems.” He is currently a collaborator for projects 13-ERD-058, “Transient Loading Effects on Structural Materials for Laser Inertial Fusion Energy;” 13-ERD-073, “Generation and Characterization of Matter at Extreme Gigabar Pressures;” 13-ERD-078, “Strength and Phase Transformation Kinetics Under Dynamic Compression;” and 15-ERD-012, “Melting and Solidification in Multicomponent Materials: Constraints on the Search for Habitable Planets.”
American Meteorological Society Fellow
In 2015, climate scientist and LDRD researcher David Bader was elected a fellow of the American Meteorological Society. Election recognizes outstanding contributions to advance atmospheric and related sciences, technologies, applications, and services for the benefit of society. A maximum of 0.2% of the society’s membership is approved annually through the fellow nomination process. Bader was the principal investigator for an LDRD project investigating regional climate (06-ERD-066) and was a co-investigator for another effort examining regional climate change prediction for the 21st century (09-ERD-055). Earlier in 2015, Bader also earned a DOE Secretarial Honor Award for his leadership of the Accelerated Climate Modeling for Energy project. The Secretarial Honor Awards are the department's highest form of non-monetary employee recognition. The Accelerated Climate Modeling for Energy project is a multi-institutional effort involving eight DOE national labs, the National Center for Atmospheric Research, four academic institutions, and one private-sector company. The project accelerates the development and application of fully coupled, state-of-the-science Earth-system models for scientific and energy applications.
Leibniz Prize
Former LDRD researcher and current Deutsches Elektronen-Synchrotron Professor Henry Chapman was awarded one of the prestigious Gottfried Wilhelm Leibniz Prizes in 2015 by the German research foundation Deutsche Forschungsgemeinschaft. This important research award in Germany honors outstanding scientists. Henry Chapman received the 2.5-million-Euro prize for his pioneering work in the development of femtosecond crystallography. It enables the decoding of complex biomolecule structures in their native configuration with the help of x-ray lasers. The femtosecond crystallography methods that lead to this award were originally pioneered by Chapman and his colleagues at Livermore with funding from LDRD under projects 02-ERD-047, "A Revolution in Biological Imaging" and 05-SI-003, "Biological Imaging with Fourth-Generation Light Sources."
Fusion Power Associates Awards
Livermore LDRD researchers Susana Reyes and Wayne Meier were among the recipients of the annual Fusion Power Associates awards for 2015 by the Fusion Power Associates Board of Directors. Fusion scientist Wayne Meier has been awarded a Special Award, which has been given periodically since 1980 to recognize individuals who have made a special contribution to the cause of fusion power development. Nuclear engineer Susana Reyes was selected as the recipient of its 2015 Excellence in Fusion Engineering Award. This award has been given annually since 1987 to recognize researchers in the relatively early part of their careers who have shown both technical accomplishment and the potential to become exceptionally influential leaders in the fusion field.
- Reyes, currently the LDRD principal investigator for a next-generation process for tritium recovery from fusion power plant blankets (13-ERD-056), was cited for "the leadership she has been providing to both magnetic and inertial fusion efforts in many areas, including safety and licensing, tritium systems and power plant designs." She was also acknowledged for "the important role she played in the National Academy's panel on Prospects for Inertial Confinement Fusion Energy Systems, and as chair of the American Nuclear Society Fusion Energy Division.”
- Meier, the principal investigator for a concluding LDRD project on ternary alloy development for enhanced safety and performance of fusion systems (14-ERD-035), was cited for his "many contributions to advancing the science, technology, and integrated assessments of potential fusion power plants, and for broad support of the fusion community in leadership positions within the American Nuclear Society and Institute of Electrical and Electronics Engineers," as well as his role on journal editorial boards.
Senior Members of SPIE
Lawrence Livermore researchers Nerine Cherepy and Michael Pivovaroff are among 117 new senior members of SPIE, the international society for optics and photonics. SPIE senior members are members of distinction who are recognized for their professional experience, their active involvement with the optics community and SPIE, or significant performance that sets them apart from their peers.
- Cherepy, a research staff member of the Materials Science Division at Livermore, is being recognized for her “achievements in discovery and development of new scintillator materials and detectors.” She has served as an investigator for a number of LDRD projects dating back to 2000 concerning direct conversion of fossil fuels into electricity (00-ERD-059), photochromic radiation dosimetry (03-ERD-040), high-performance polymer waveguides (09-ERD-057), and advanced radiation detectors for weak signals (10-SI-015). Currently, she is a co-investigator for a project exploring the fabrication of functionally graded optical components using additive manufacturing (16-SI-003).
- Pivovaroff, a Livermore physicist, is honored for his “achievements in design, fabrication, and use of reflective x-ray optics.” He has been an investigator for several LDRD projects since 2003 concerned with nondestructive characterization, x-ray optics and mirrors, advanced radiography, and radiation detectors for weak signals. He is currently the principal investigator for a project investigating use of cooperative constellations of small satellites to perform space missions important for U.S. national security (14-SI-005).
Joseph Weber Award for Astronomical Instrumentation
Claire Max, an astrophysicist at Livermore and now a faculty member at the University of California at Santa Cruz, earned the 2015 Joseph Weber Award for Astronomical Instrumentation from the American Astrophysical Society for her adaptive optics work. Max was awarded for co-inventing sodium laser guide-star adaptive optics and for shepherding it from its roots in space surveillance to an essential technology on large telescopes. Max's adaptive optics work was supported by LDRD under project 91-DI-008, investigating laser guide stars. Her leadership transformed how astronomers work by making near-diffraction-limited imaging possible on large ground-based telescopes, thus opening new fields of discovery. Her work on laser guide stars resulted in a ground-based astronomy revolution. She also directed the implementation of these artificial guide stars at astronomical observatories, including the Lick and W. M. Keck observatories in California and Hawaii, respectively.
R&D 100 Awards
In 2015, LDRD-supported technologies received two of three awards presented to the Laboratory in the R&D 100 Awards competition. The process to select the winners, chosen for their commercial potential or enduring value they will bring to the nation, is demanding and takes almost a year. Only 100 entrants are singled out, yet remarkably, year after year the Laboratory is listed more than once on the roster of winners. Since LLNL began submitting entries in 1978, it has received over 150 of these awards. This continuous recognition epitomizes science and technology in the national interest.
- Large-Area Projection Micro Stereolithography. A three-dimensional printing device, this technology is an image projection system. It rapidly produces very small features over large areas by using optical techniques to write images in parallel, as opposed to conventional techniques. It combines the advantages of laser-based stereolithography (large area and speed, but lower resolution) and digital light-processing stereolithography (fine details and speed but only over a small area), enabling the rapid printing of fine details over large areas. The LDRD project 08-ERD-053, “High-Resolution Projection Microstereolithography for Advanced Target Fabrication,” provided early support for this R&D award winner. Its purpose was to create a three-dimensional fabrication technique to advance laser target fabrication as well as micro-fabrication technology. The Large-Area Projection Micro Stereolithography system is conceptually similar to building a mosaic of tiles that combine to make a much larger picture. Each one of the tiles has significant detail and they fit together to form the picture that, in turn, has significantly more detail. Many applications would benefit from the capability to create complex shapes and small features, unlike other state-of-the-art three-dimensional printers, which sacrifice overall part size in exchange for small feature size. Parts produced with this system can be used as master patterns for injection molding, thermoforming, blow molding, and various metal-casting processes. Some of the other commercial applications envisioned for the system include medical devices, dentistry, and microfluidics.
- High-Power Intelligent Laser Diode System. This new laser pumping system employs advances in laser diodes and electrical drivers to achieve two-to-three-fold improvements in peak output power and intensity over existing technology. It is also 10 times more compact and can scale to even larger arrays and power levels. With early support from LDRD project 13-SI-001, “Giga-Shot Optical Laser Demonstrator,” a team of LLNL scientists and engineers, in partnership with Tucson, Arizona-based Lasertel, developed the system, which has produced 3.2 MW of peak optical power from four pump systems at a 20-Hz repetition rate in its largest power output to date. Pulsed laser diode arrays such as this are essential for pumping high-energy solid-state lasers at frequencies above 5 Hz for materials processing such as laser peening, defense applications, and scientific exploration. The High-Power Intelligent Laser Diode System is being deployed on the high-repetition-rate, petawatt laser system that LLNL is developing for the European Light Infrastructure initiative, which will use high-energy diode pumped lasers to study light–material interaction physics, with expected spinoffs for industrial and medical technologies. The technology improves upon other laser technologies by providing significantly more optical power at significantly higher intensity in a system with a substantially smaller footprint and a higher degree of integration. These developments enable the creation of more energetic laser systems that exhibit higher electrical efficiency.
Far West Technical Transfer Award, Federal Laboratory Consortium
Byran Moran, a co-investigator for LDRD project 14-SI-004, “Deterministic Multifunctional Materials and Manufacturing Initiative,” was awarded a 2015 Federal Laboratory Consortium’s Far West Technical Transfer Award for outstanding technology development. The award was given for the Large-Area Projection Micro Stereolithography technology, which also won a 2015 R&D 100 Award and received early support from LDRD project 08-ERD-053, “High-Resolution Projection Microstereolithography for Advanced Target Fabrication.” Many applications would benefit from the technology’s capability to create complex shapes and small features. Current state-of-the-art three-dimensional printers sacrifice overall part size in exchange for small feature size. Commercial applications envisioned for the system include medical devices, dentistry, and microfluidics. The system has garnered significant attention from potential users and collaborators, and is considered an excellent candidate for technology transfer. Started in 1974, the Federal Laboratory Consortium assists the U.S. public and private sectors in utilizing technologies developed by federal government research laboratories. It is comprised of more than 250 federal government labs and research centers.
America Makes Award
The Laboratory, in collaboration with General Electric, has been awarded a $540K America Makes grant to develop open-source three-dimensional printing algorithm software. America Makes, a Youngstown, Ohio-based institute, has been focused on enhancing the nation's competitive position in the additive manufacturing field. The award is intended to bring the resulting algorithms into use in both the public and private sectors, encouraging more participation in additive manufacturing using metal, with a focus on selective laser melting methodology. At present, while the technology is clearly promising and many organizations are working with and improving upon the technique, there is no single approach common among all users. This lack of common ground has been holding it back from reaching its full potential. Efforts that led to the award were supported by LDRD project 15-ERD-037, “Physics of Laser-Assisted Advanced Manufacturing Processes,” with Manyalibo Matthews serving as the principal investigator.
NASA Group Achievement Award
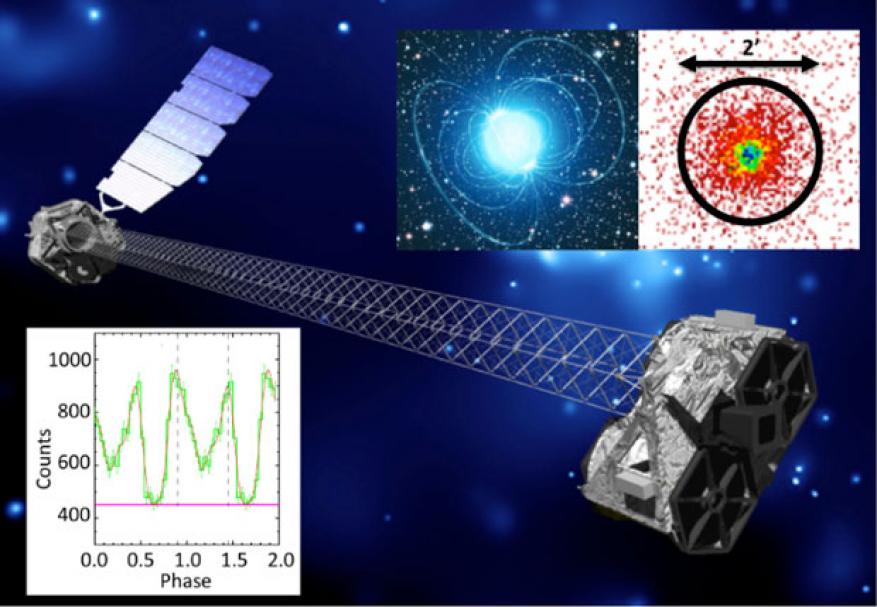
In 2015, LDRD principal investigators Julia Vogel and Michael Pivovaroff received the NASA group achievement award for the NuSTAR Project Team. The work was supported by the “Neutron Star Science with the Nuclear Spectroscopic Array” (13-ERD-029) LDRD project. The NuSTAR mission has advanced our understanding about how galaxies in the universe form and evolve, and observed some of the hottest, densest, and most energetic objects in the universe, including black holes, their high-speed particle jets, supernova remnants, and the Sun. The LDRD project also received the Group Achievement Award in 2013 and 2014.
Livermore Entrepreneurs’ Hall of Fame
Two former Lawrence Livermore LDRD researchers—Bill Colston and Fred Milanovich—were inducted into Livermore's Entrepreneurs’ Hall of Fame. The researchers, who represent half of the second class of inductees, were honored for developing technologies during or after their Laboratory careers that created major economic impacts and spawned influential companies. They received support from LDRD for research while at Livermore, including projects 03-FS-008, “Single-Use Real-Time Bioweapons Detector” and 03-SI-005, “Pathomics” (Colston) and project 99-SI-016, “Broad Spectrum Biological Assays Using Liquid Based Detection Arrays” (Milanovich). In 2008, Colston and Milanovich founded QuantaLife, Inc. in Pleasanton, California, a company focused on deploying sensitive and accurate genetic-testing technology. In 2011, the company was acquired by Bio-Rad Laboratories—a biomedical technology company located in Hercules, California—for $162M.
Best Paper, U.S. Rock Mechanics/Geomechanics Symposium
A report examining how particles injected into underground fractures maximize energy resource extraction won the best paper award at the 49th U.S. Rock Mechanics/Geomechanics Symposium in San Francisco, California, in June 2015. The award recognizes the outstanding contributions to the conference, and selection criteria include originality of the technical work, innovation, potential practical value, and clarity of presentation. “Proppant Transport at the Fracture Scale: Simulation and Experiment” was presented by Pratanu Roy, and coauthored by Wyatt Du Frane and Stuart Walsh. The paper is based on research conducted as part of the LDRD project by Livermore scientists Roger Aines and Jeff Roberts on reactive materials for hydraulic fracturing (13-ERD-029). Proppants typically are sand particles used to ensure that fractures created in rock remain open after hydraulic fracturing. Correct proppant placement is key to maintaining fracture permeability following hydraulic stimulation of geological resources, particularly in stimulating unconventional oil and gas reservoirs. The nature of proppant transport in natural fractures is poorly understood, so the authors employed a combination of high-fidelity numerical simulations and fracture-scale experiments to describe the transport properties of proppants. The experimental work examines proppant movement in clear-plastic three-dimensional reproductions of the shale surfaces recreated using three-dimensional printing.
Best Paper, International Symposium on Memory Systems
Maya Gokhale received a best paper award for her work on LDRD project 13-ERD-025, “Data-Centric Computing Architecture” at the International Symposium on Memory Systems held in Washington, D.C., in October 2015. The symposium is devoted to exploring improvements in the computing memory system that can have significant impact on power and energy, performance, and cost. The project focused on anticipating the unfolding revolution in memory technology by pursuing research to devise system software and memory hardware to optimize memory access for both data science and scientific applications. Key targets were capacity and irregular, cache-unfriendly access.
Journal Covers
In addition to the numerous awards LDRD researchers garner each year, innovative science, technology, and engineering is evidenced by both the number of scientific journal articles and front-cover features in high-visibility journals documenting LDRD Program project results. In FY15, several LDRD projects were featured on the covers of peer-reviewed journals.
The December 1, 2014 edition of Applied Physics Reviews features on its cover an invited review paper describing the developments and scientific application of the dynamic transmission electron microscope. Development of the instrument was initially supported by an LDRD project on time-resolved transitions via dynamic transmission electron microscopy (06-ERD-007). The series of cover images depict crystallization occurring on the microsecond time scale, captured using the "movie mode" of Livermore's dynamic transmission electron microscope. The paper covers the history of the instrument’s technology, starting with pioneering work at the Technical University of Berlin in the 1970s through the 1990s, continuing with LLNL’s successful construction of the microscope, and culminating in the most recent advancement of the technique that enables capture of ultrafast events as they unfold. The paper also reviews the wide range of scientific investigations enabled by the microscope, such as the precise measurement of phase-change kinetics, morphological evolution during the breakup of thin films, and microstructural development during rapid solidification after melting, an issue highly relevant to additive manufacturing.
The sophistication and large functional repertoire of biomolecules inspired Livermore researchers to use them in hybrid bio-electronic devices to create interfaces between synthetic and biological systems. The Livermore LDRD team, and various university and national laboratory collaborators, documented the construction and operation of a bio-electronic device that couples light-driven proton transport with an electronic circuit output. Their work was published as a cover article in the February 2, 2015 issue of Advanced Materials. The team covered a silicon nanowire transistor with a lipid bilayer containing bacteriorhodopsin, which when exposed to green light, transfers protons across the bilayer, decreasing the pH near the nanowire. The resulting change in the surface charge causes a change in the transistor output. Incorporation of other molecules in the bilayer was shown to change the bilayer’s potential and alter its permeability to various ions. These results open opportunities for constructing bio-electronic devices, particularly ones based on biological processes powered by pH gradients, and provides an extensive toolkit for applications such as implantable biosensors and neural interfaces. The Livermore portions of this work were funded by project 12-ERD-073, “Carbon Nanometer-Scale Membrane Channels.”
Featured on the February 16, 2015 cover of Chemical Physics Letters, LDRD researcher Nir Goldman’s work on the development of many-body density functional “tight-binding” models for carbon extends the use of the technique for extremely fast and accurate quantum calculations of materials under extreme conditions. The method was applied to simulations of exotic high-pressure phases of carbon, and yielded results with a small fraction of the computational effort of standard quantum simulation approaches. The results indicate a straightforward approach by which many-body effects can be included in density functional tight binding, thus extending the method to a wide variety of systems and thermodynamic conditions. This work was supported by an LDRD project that examined the equation of state of polymers under extreme conditions with quantum accuracy (12-ERD-052).
Livermore LDRD researcher Manyalibo Matthews and colleagues describe the techniques they developed to remove surface flaws on laser optics using localized infrared laser heating in a cover article for the March 2015 issue of Advanced Engineering Materials. Work was supported by the Laboratory’s LDRD Program under project 14-ERD-098, “Laser–Matter Coupling Mechanisms Under Varying Chemical and Particulate Configurations,” as well as project 11-ERD-026, “Chemical-Vapor-Modified Laser-Based Damage Mitigation and Surface Shaping of Fused Silica.” Such surface flaws tend to limit performance in high-power laser systems. The paper presents results of using infrared laser light to polish, anneal, and microscopically shape fused silica surfaces. The team has shown that the resulting material response can be “tuned” by considering the temperature-dependent optical constants of the material and by choosing the appropriate set of laser parameters. The results are relevant beyond their immediate application to damage mitigation in high-energy laser systems and can be used for any application that requires laser smoothing and shaping of silica surfaces.
Featured on the cover of the March 4, 2015 issue of Advanced Materials is research by a team of Livermore researchers and colleagues at Lawrence Berkeley National Laboratory and the National Institute of Advanced Industrial Science and Technology in Japan. The team reports on the use of a newly developed, synchrotron-based x-ray adsorption spectroscopy technique that enables characterization of the complex, electric-field-induced changes in electronic structure that carbon-based super-capacitor electrodes undergo during a charge and discharge cycle. The LLNL team was funded, in part, by LDRD under projects 10-LW-045, “In Situ Spectroscopy and Microscopy for the Study of Advanced Materials for Energy Storage” and 12-ERD-035, “Dynamically Tunable Nanometer-Scale Materials: From Atomic-Scale Processes to Macroscopic Properties.” Future energy-storage systems will need to have much larger storage capability, rapid charge and discharge cycling, and improved endurance. Progress in these areas demands a more complete understanding of energy-storage processes at atomic through micron-length scales. Because these processes can change significantly as the system is charged and discharged, researchers have increasingly focused on ways to characterize an operating energy-storage system. The electronic structure of graphitic carbon super-capacitor electrodes can be tailored by charge-induced electrode–electrolyte interactions, and opens a path towards more efficient electrochemical energy-storage systems. The experimental and modeling techniques developed for this work can be readily applied to other energy-storage materials and technologies.
Appearing on the cover of the March 31, 2015 issue of Langmuir, a Livermore project was featured that is developing a method for precise particle assembly with single-particle precision using electrophoretic deposition in combination with a patterned electrode template. The technique is an externally forced assembly process that has been shown to be capable of manipulating a wide range of materials. An electrode with differently sized hole patterns, from 0.5 to 5 μm, was used to demonstrate the ability to control particle deposition events based on the applied voltage and particle-to-hole size ratio. With decreasing hole size, a larger electric field was required for a particle deposition event to occur in that hole. The likelihood of particle deposition continued to increase for smaller-sized holes as the electric field was increased. Eventually, a monolayer of particles began to form, and a voltage threshold was found for each hole pattern of different size, allowing adjustments in pattern hole size and voltage to control when a particle deposition event took place on a given electrode pattern. This phenomenon opens the path to controlled, multiple-material deposition and assembly onto substrates without re-patterning of the electrode or complicated surface modification of the particles. The research was supported by LDRD projects “Manipulation of Surface Plasmon Resonance by Programmable Nanometer-Scale Particle Assemblies,” (13-LW-006) and “Deterministic Multifunctional Materials and Manufacturing Initiative” (14-SI-004).
One of the major challenges of operating high-energy laser systems such as Livermore's National Ignition Facility is mitigating laser damage to the silicon dioxide fused-silica optics used in the system. High irradiance levels near the laser damage threshold of the optics can create small pits in an optic’s surface. In the cover article for the August 2015 issue of Laser Focus World, LDRD researcher Manyalibo Matthews describes use of a software tool for modeling and simulating physics-based problems to study techniques for repairing and recycling damaged optics. The simulations included heat transfer in fluids, chemical reactions, and structural mechanics, as well as mass transport and fluid flow. Work was partially supported by an LDRD project studying laser–matter coupling mechanisms under varying chemical and particulate surface configurations (14-ERD-098).
A September 2015 issue of The Journal of Physical Chemistry C featured research by LDRD investigator Nir Goldman and colleague Christopher Cannella, an undergraduate summer researcher from Caltech, on a way to create linear chains of carbon atoms from laser-melted graphite. Their computational investigation of carbyne, which has been called the strongest material in the world, is part of an intense research effort because of its presence in astrophysical bodies, as well as potential for use as a nanometer-scale electronic device and for hydrogen storage. Carbyne is a chain of carbon atoms held together by either double or alternating single and triple atomic bonds. Using an efficient, semi-empirical quantum mechanical computational method known as density-functional tight binding, Cannella and Goldman modeled the melting and vaporization of graphite on a nanosecond timescale. With their LDRD project on the “Equation of State of Polymers Under Extreme Conditions with Quantum Accuracy” (12-ERD-052), Goldman and his team optimized new density-functional tight-binding models, thereby creating a general capability for simulating carbon–hydrogen–oxygen bonded systems under pressures up to 20 Mbar and temperatures up to 3 eV. Goldman’s study and computational models allow for direct comparison with experiments and can help determine parameters for synthesis of carbon-based materials with potentially exotic properties. Carbyne’s linear shape gives it unique electrical properties that are sensitive to stretching and bending, and is 40 times stiffer than diamond.
High dielectric-constant multilayer coatings are commonly used on high-reflection mirrors for high-peak-power laser systems because of their high laser-damage resistance. However, surface contaminants often lead to damage upon laser exposure, thus limiting the mirror’s lifetime and performance. One plausible approach to improve the overall mirror resistance against laser damage, including that induced by laser–contaminant coupling, is to coat the multilayers with a thin, protective capping layer on top of the multilayer coatings. An understanding of the underlying mechanism by which laser–particle interaction leads to capping layer damage is important for the rational design and selection of capping materials of high-reflection multilayer coatings. In the cover article for the October 10, 2015 issue of Applied Optics, Livermore researchers describe how laser damage testing at oblique incidence shows that laser–contaminant interaction on high-reflection multilayer coatings leads to damage to the surface layer, with the severity directly related to thermal properties of cap materials and particle shape. Work was partially supported by the LDRD project “Laser–Matter Coupling Mechanisms Under Varying Chemical and Particulate Surface Configurations” (14-ERD-098).