Geoffrey Oxberry (16-ERD-025)
Executive Summary
We are exploring approaches to topology optimization that can be used to analyze thousands of manufacturing-defect scenarios and, in the process, develop optimized designs that are robust even for the largest defect scenarios. The result of this more comprehensive characterization of manufacturing defects could accelerate materials-certification efforts, increase materials reliability, and help assess the impact of enhanced manufacturing control strategies.
Project Description
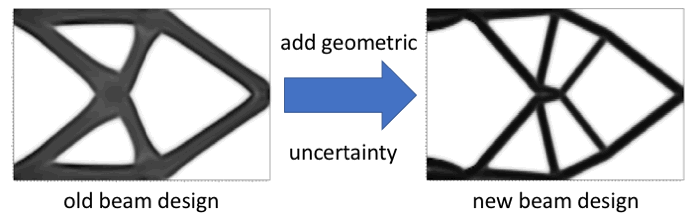
Additive manufacturing has enabled the development of novel high-performance materials because of its inherent high degree of control over shape and composition at fine length scales. For the design of structured materials with novel properties, topology optimization is used to compute the best shape by optimizing a given objective such as stiffness, subject to given constraints such as mass or volume. We are designing materials by calculating the shape (topology optimization) that gives the optimal performance (e.g., in structural applications or compliance) subject to constraints and manufacturing uncertainty. We are developing the most accurate method to date to overdesign additively manufactured materials to compensate for manufacturing defects and accelerate manufacturing certification. We are employing recently developed state-of-the-art parallel algorithms to solve problems in topology optimization under uncertainty containing the most accurate characterization of defects to date. Specifically, we are designing methods for topology optimization that can analyze thousands of manufacturing-defect scenarios and, in the process, design for the average of the worst five percent of defect scenarios. The target application is electronic multifunctional materials that have a structural function (load-bearing) and an electromagnetic function (electromagnetic radiation propagated in specified ways, such as cloaking).
We expect to provide a capability to design multifunctional materials in three dimensions under uncertainty using topology optimization by characterizing the uncertainty using a thousand or more representative random samples of manufacturing defects, which is an order of magnitude more samples than achieved in the literature for two-dimensional design. We are developing a topology-optimization code that solves coupled linear elasticity and Helmholtz equations, which applies the technique of separation of variables to reduce the complexity of the analysis, to model both the deformation of the material under load and the propagation of electromagnetic waves of given frequencies through the material. To our knowledge, our approach will be the first to design both structural and electromagnetic properties of these engineered materials. We are developing this method using stochastic programming, an approach that accounts for uncertainty by incorporating the statistical distribution of known uncertainties in optimization problems. Recently developed algorithms in stochastic programming and unique parallel computing resources now make this approach possible. The result of this more comprehensive characterization of manufacturing defects could accelerate materials-certification efforts, increase materials reliability, and help assess the impact of enhanced manufacturing control strategies.
Mission Relevance
This project—the creation of a design process via a topology-optimization stochastic programming code that accounts for manufacturing variability in multifunctional materials—supports the Lawrence Livermore National Laboratory and NNSA's mission to develop new, high-performance materials rapidly. Specifically, this process could accelerate the materials-certification process by providing statistical guarantees regarding material performance, even in the presence of manufacturing defects. This work, therefore, supports the Laboratory’s core competency in advanced materials and manufacturing through the use of high-performance computing, simulation, and data science, as well as the DOE's goal to deliver major scientific tools that transform our understanding of nature and strengthen the connection between advances in fundamental science and technology innovation.
FY17 Accomplishments and Results
In FY17 we (1) developed a new parallel algorithm (HiOp) to solve large-scale topology optimization problems with a small number of complicating constraints and enable us to solve design-optimization problems 10 to 100 times larger than we could with the commercial off-the-shelf library Interior Point OPTimizer (known as "IPOPT") software package for large-scale nonlinear optimization; (2) improved the structural-optimization code so that it can solve design problems with approximately two million design variables over 256 cores, import meshes from Cubit software used for the generation of two- and three-dimensional finite-element meshes (grids) and geometry preparation, add surface loads, and add repeating unit cells for designing metamaterials (i.e., engineered materials with properties not found in nature); (3) implemented a Monte Carlo uncertainty quantification capability for random loading; and (4) released our code to our academic collaborators.
Publications and Presentations
Oxberry, G. M., et al. 2017. "Topology Optimization Using Conditional Value-at-Risk." Modeling and Optimization: Theory and Applications (MOPTA), Bethlehem, PA, 16–18 August 2017. LLNL-PRES-739820.
Petra, C. G. (Forthcoming.) "A Memory-Distributed Quasi-Newton Solver for Nonlinear Programming Problems with a Small Number of General Constraints." Journal of Parallel and Distributed Computing. LLNL-JRNL-739001.