David J. Larson (15-ERD-066)
Abstract
The goal of this project was to develop and begin exploiting a new capability for self-consistent calculations of a nuclear-driven electromagnetic pulse (EMP) in three spatial dimensions. Modern assessment of EMPs is necessary for developing forensic capabilities based on signals measured in the urban and space environments, predicting the propagation of pulses through the ionosphere, and modeling three-dimensional effects due to asymmetric gamma and x-ray output from a nuclear weapon and obstacles in the environment. A suite of modern tools for simulating the generation and propagation of the prompt EMP in three spatial dimensions has been developed. These include the EMfPulse code (based on particle-in-cell methods and a Cartesian grid in the laboratory frame) and Spherical Harmonic EMP (SHEMP), a fast-running companion code that employs a vector spherical harmonic decomposition. EMPulse is a comprehensive first-principles code with full generality that requires significant computing resources. It tracks Compton electrons directly in the laboratory frame and includes Ohmic and swarm models for the evolving local conductivity. SHEMP builds on the methods used in Longmire's fast-running CHAP code (Longley and Longmire 1973; Longmire 1983) and in our own CHAP-lite. In those codes, one-dimensional spherical symmetry is assumed, and the calculation takes advantage of a separation of scales. In SHEMP we achieve similar efficiencies in three dimensions, incorporating non-spherically-symmetric physics via a pseudo-spectral approach.
Background and Research Objectives
The essential physics involved in the generation of an EMP has long been known (Karzas and Latter 1965; Longmire 1978, 1983, and 1986). The energetic gamma rays emitted by nuclear reactions propagate through the atmosphere until they interact with neutral atoms, producing ions and energetic Compton electrons. The electrons turn in the Earth's magnetic field, generating a coherent current that produces a large electromagnetic signal via synchrotron radiation.
First-generation codes that model this physics, such as CHAP (Longley and Longmire 1973, Longmire 1983) and HEMP (Page et al. 1975), assume one-dimensional spherical symmetry and make other simplifying assumptions. These codes cannot treat the important effects of gamma shadowing, wherein an obstruction shields a region of space from some or all of the gamma pulse. In the shadowed region, a reduction in the number of Compton and secondary electrons causes a reduction of the conductivity and less attenuation of the EMP pulse (most of which may come from the unshadowed region). The result may be a significant increase in the field amplitude.
We developed two new three-dimensional (3D) codes for modeling EMPs. Starting with the Warp particle-in-cell (PIC) code (Friedman et al. 1992; Grote et al. 2005), which was developed by our team members, we added EMP-specific models: sources (gammas, Compton electrons), air evolution (including avalanche ionization), and a simple geomagnetic field model to develop EMPulse (a first-principles code with full generality). Seeking the efficiencies inherent in legacy codes like CHAP, we developed the Spherical Harmonic EMP (SHEMP) code utilizing a pseudo-spectral electromagnetic-field solver.
Scientific Approach and Accomplishments
Our initial investigations focused on the basic physics of EMP generation and propagation (Farmer and Friedman 2015; Farmer et al. 2016). We first examined the accuracy of the obliquity factor (Longley and Longmire 1973), an analytic approximation, in modeling multiple scattering of the Compton electrons. The obliquity factor, Monte Carlo, and Fokker-Planck finite-difference methods were compared. Skewness occurs in the velocity distribution due to the Doppler effect. We demonstrated that the obliquity factor does not correctly capture this skewness, but the Monte Carlo and Fokker-Planck finite-difference approaches do. Including the initial Klein-Nishina distribution of the electrons and the momentum dependence of both drag and scattering led us to conclude that the obliquity factor is adequate for most situations. However, as the gamma energy increases and the Klein-Nishina distribution becomes more peaked in the forward direction, skewness in the distribution causes greater disagreement between the obliquity factor and a more accurate model of multiple scattering. We examined the effects of including the single-scattering tail in the scattering distribution and the radial derivative of the backward-traveling wave on the production of EMP signals. We found that including these effects caused a discrepancy between field amplitudes of two to three percent and a 10-percent discrepancy between rise times. We concluded that the biggest factor in determining the rise time of the EMP signal is the conductivity, not the dynamics of the Compton current.
EMPulse is a comprehensive first-principles code (Friedman et al. 2016, Friedman et al. 2017) with full generality and requiring significant computing resources. It tracks Compton electrons in the laboratory frame and includes Ohmic and swarm models for the evolving local conductivity. It is intended to enable detailed and self-consistent study of multi-dimensional effects in geometries that have in general been treated approximately. EMPulse builds upon the Warp PIC code base, in particular its 3D electromagnetic PIC methods. It uses a mixture of the Fortran and Python programming languages; input files are Python-based programs and the code can be run interactively. Users rarely alter the underlying Fortran code, but often add functionality via Python.
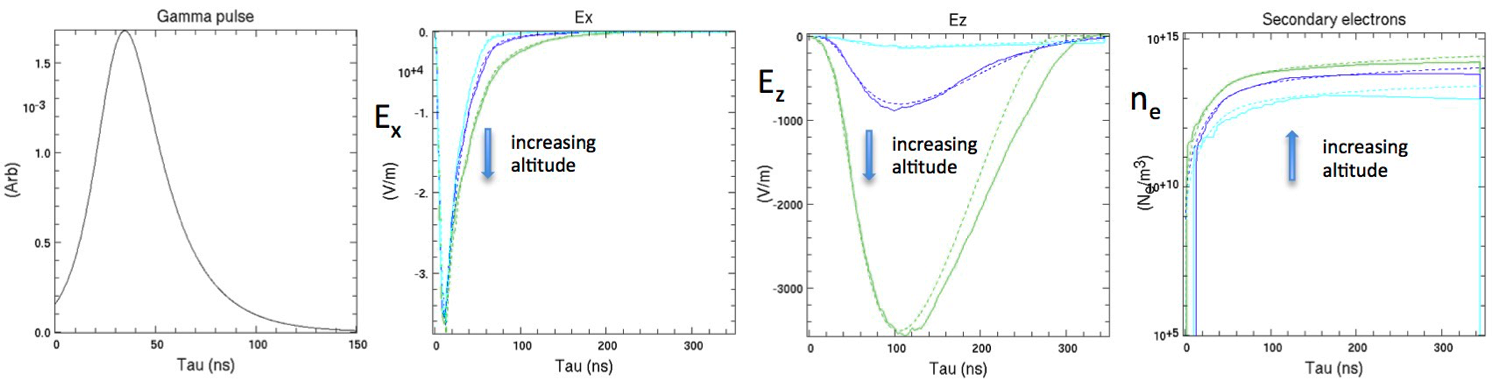
As we developed the models in EMPulse, we continued to benchmark them against CHAP-lite. Figure 1 compares simulations in planar geometry of downward EMP from a 1-kT burst at 30 km using Longmire's "nominal" analytic Starfish gamma-pulse profile (Longmire 1985) and a gamma energy of 1.6 MeV, showing good but not perfect quantitative agreement between the codes. Though the EMPulse run was 3D, currents were averaged over the transverse coordinates to minimize the statistical noise resulting from use of a modest peak number (105) of simulation particles (Compton electrons); with periodic boundary conditions in x and y, this yields a one-dimensional result, as in CHAP-lite (which was modified to run in planar geometry for this comparison). Earlier tests using standard “Yee" differencing of the Maxwell equations suffered from excessive numerical dispersion, so this EMPulse run used the Cole-Karkkainen prescription (Cole 2002; Karkkainen et al. 2006), which is dispersion-free along the grid axes.
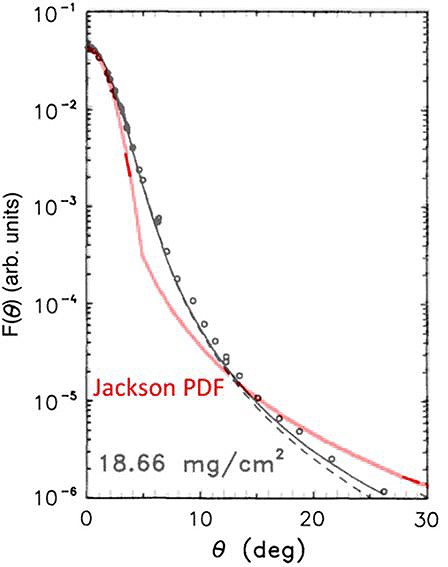
The Monte Carlo collision operator that computes the drag and scatter of the Compton electrons in air was upgraded to include large-angle single scattering using a new algorithm (Cohen et al. 2017; Higginson 2017) based on J. D. Jackson's method (Jackson 1999) of joining the multiple small-angle-scattering probability-distribution function (PDF) PM to the large-angle Rutherford scattering PDF PS. PM is a Gaussian with two free parameters. PS is the PDF derived from the Rutherford cross-section with no free parameters, apart from a normalized transition angle, above which the angle-scattering PDF is given by PS and below which the PDF is given by PM. The algorithm determines the two free parameters and the transition angle by simultaneous iterative solution of three constraint relations: (1) the overall normalization of the composite angular PDF is unity, (2) the variance of the angular PDF is a constant determined by the scattering parameters, and (3) the composite PDF is continuous when the scattering angle equals the transition angle. Solutions for the three constants were produced outside the simulation and tabulated as functions of particle energy and altitude, so that table look-up and interpolation are used within the Monte Carlo collision routine. A comparison of the angular-scattering routine's results to the experimentally measured angular-scattering PDF for a gold foil experiment (Hanson et al. 1951) and to other theories (Goudsmit and Sanderson 1940; Moliere 1947) is shown in Figure 2. Keeping in mind that joining PM to PS to construct a composite PDF is somewhat ad hoc and in the spirit of an efficient interpolation scheme, there is reasonable semiquantitative agreement with the other theories and experiment over a range of four orders-of-magnitude in the value of the PDF and a range of 30 degrees in angle.
Figure. 2. Comparison of the scattering-angle PDF (red curve) using the extension of Jackson’s (1999) theory to Goudsmit and Sanderson (1940) distributions (solid curves), distributions using Moliere’s (1947) theory (dashed curve), and experimental data (circles) from Hanson et al. (1951) for a 15.7 MeV energy electron beam incident on 18.66 mg/cm2 Au (Z = 79) foil.
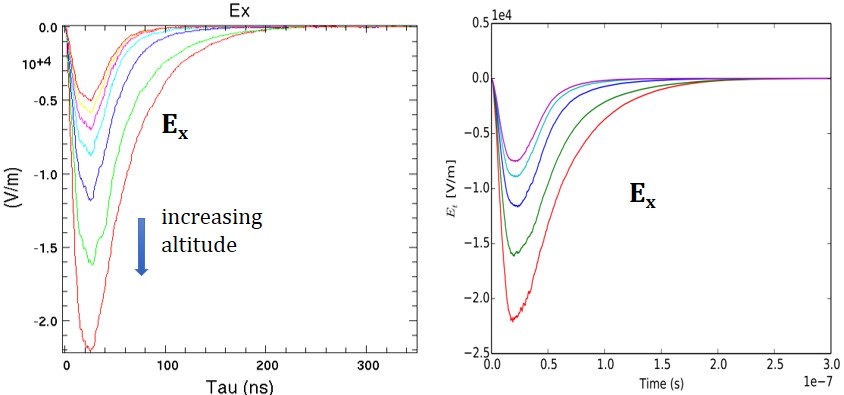
Another feature of EMPulse is the option to enable the spherical spreading of the EMP away from the burst, but in a quasi-one-dimensional approximation. This option allows the computation of the EMP along a line of sight away from a burst, resulting in a more realistic computation of the EMP amplitudes at a distant observer and facilitates more direct comparisons to CHAP and CHAP-lite. A comparison of a quasi-one-dimensional EMPulse simulation to a CHAP-lite simulation is shown in Figure 3 for a 1-kT burst at 30 km propagating to the ground, with the Starfish gamma profile, 1.6 MeV gamma energy, 0.3 percent conversion of the yield to gammas, 0.6 G applied magnetic field, and Cole-Karkkainen finite-differencing. Semi-quantitative agreement between the simulation results in EMPulse and CHAP-lite (radial geometry) is observed.
Figure 3. Comparison from quasi-one-dimensional spherical EMPulse (left graph) and CHAP-lite (right graph) simulations of the electromagnetic pulse (EMP) transverse electric field Ex versus retarded time for various altitudes during the propagation. CHAP-lite: 26.5 km (red curve), 23.8 km (green curve), 20.6 km (blue curve), 17.8 km (cyan curve), and 15.7 km (magenta curve). EMPulse: 26.55 km (red curve), 23.6 km (green curve), 20.65 km (blue curve), 17.7 km (cyan curve), and 14.75 km (magenta curve).
SHEMP builds on methods used in Longmire's fast-running CHAP code (Longmire 1978; Longley and Longmire 1972) examined in our earlier studies (Farmer and Friedman 2015) and used in our own CHAP-lite (Farmer et al. 2016). In those codes, the calculation uses a co-moving time-like coordinate to take advantage of the relatively slow variation of the key physical quantities with distance from the burst. The above-mentioned models are one-dimensional with assumed spherical symmetry; SHEMP obtains similar efficiencies in three dimensions. Non-spherically-symmetric physics is incorporated via a pseudo-spectral approach based on vector spherical harmonics.
SHEMP uses a grid in "ϒ, θ, φ" (i.e., upsilon, theta, and phi) coordinates for local quantities such as the conductivity, and a vector-spherical-harmonic decomposition of the sources and fields. For each harmonic, the radial equation is like that in CHAP-lite. Spherical harmonics represent a natural decomposition for scalar fields on the surface of a sphere. Analogous to Fourier transforms in a two-dimensional Cartesian space, each harmonic Yim carries two indices, l and m, which together describe functional variation with θ polar angle (colatitude, relative to any chosen polar axis) and azimuthal angle φ (longitude). While m is effectively an azimuthal mode number, the θ dependence of modes with the same l varies with m. In our case, we also need to account for radial variations.
Packages that transform a vector field to and from harmonic space are available; SHEMP currently uses the open-source package SHTns (Schaeffer 2013) to transform the 3D fields on each spherical shell of SHEMP’s grid into or out of l and m space. That is, from the vector field A(ϒ, θ, φ) at a particular radius ϒ, SHTns computes the spherical harmonic coefficients for each (l,m) pair. SHTns also performs the reverse (“synthesis”) transform, yielding the fields at every point on the spatial grid at the current radius ϒ.
The physics of CHAP is neatly encapsulated in this formulation. For radial fields, the spherically symmetric (0,0) harmonics suffice, while for the (usually dominant) transverse fields, the first non-vanishing term involves l = 1 modes. Note that we need not decompose that field into harmonics; it is needed for “local” physics (i.e., Compton orbits) at the nodes, but it does not influence the Maxwell advance because it is static.
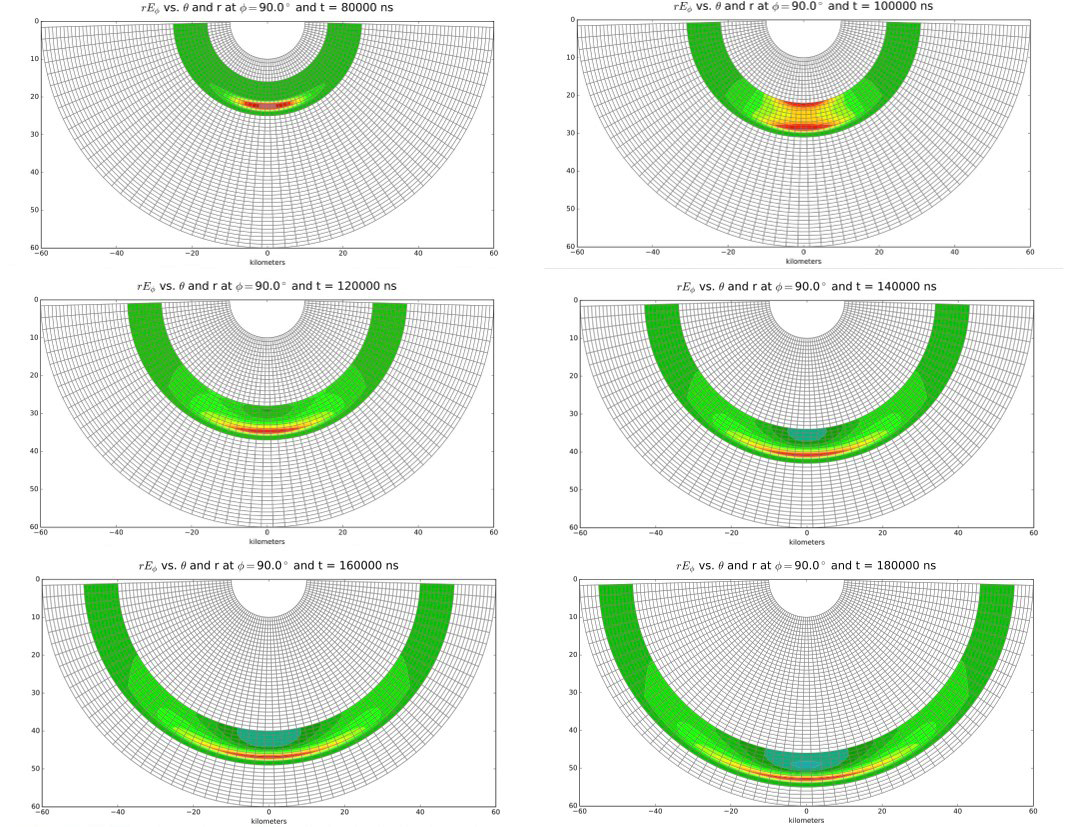
A Maxwell solver embodying this formalism has been implemented in SHEMP. Figure 4 shows the propagation of rEφ driven by a φ-directed localized source. Note that by including the factor of r, we scale out the usual fall-off of intensity with radius. The pulse spreads only modestly in angle, as evident in the figure, and quantified by the very slow decrease of the peak amplitude.
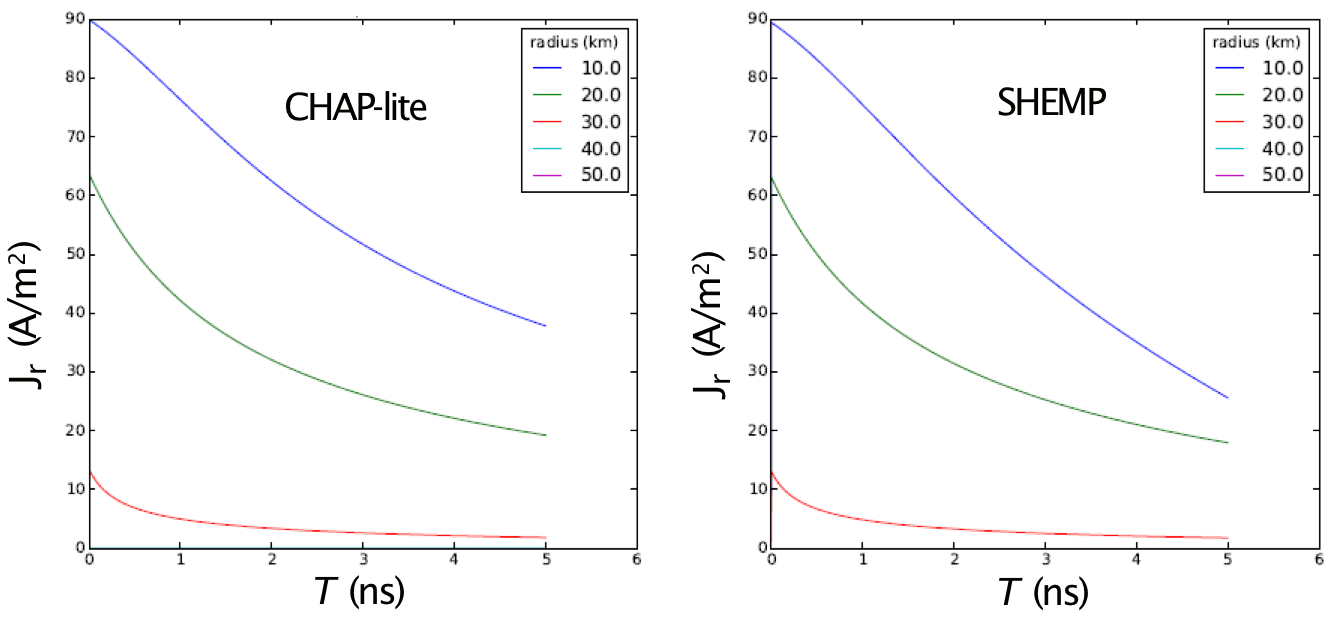
SHEMP includes an inertial swarm model for conduction current that arises to oppose the Compton current. We have compared results with CHAP-lite and demonstrated reasonable agreement for the early-time evolution of the EMP pulse, as shown in Figure 5.
The codes we developed for simulating the EMP pulse bring complementary capabilities for accurately computing the field produced at a set of remote positions. EMPulse embodies a first-principles treatment, capable of handling fully general geometries and full self-consistency regarding sources and Compton dynamics. EMPulse simulations of large regions in full 3D call for large-scale computing resources. SHEMP takes advantage of the attributes of EMP generation and propagation, resulting in significant increases in efficiency at the expense of complete generality.
Impact on Mission
Our work supports Lawrence Livermore National Laboratory’s missions in national security and stockpile stewardship science by providing a detailed understanding of nuclear-burst effects for a range of scenarios. We also added to the country's capabilities in identifying and quantifying threats from EMPs, assessing EMP applications, developing forensics based on measured pulses, and setting hardening standards. This work also supports the Laboratory's mission of nuclear threat reduction (specifically, global monitoring and consequence management), monitoring for nuclear nonproliferation, protection of space assets, and the computational engineering associated with global security (specifically, vulnerability assessments and mitigation strategies for homeland infrastructure).
Conclusion
We succeeded in producing new 3D tools for modeling nuclear-driven EMPs. Recent interest in EMP effects on the nation’s electrical power grid has provided an avenue for continued use and development. For example, the EMPulse code has been used in a research project at the Laboratory funded by the Electric Power Research Institute.
References
Cole, J. B., 2002. “High-Accuracy Yee Algorithm Based on Nonstandard Finite Differences: New Developments and Verifications.” IEEE Transactions on Antennas and Propagation 50(9): 1185—1191. doi: 10.1109/TAP.2002.801268.
Cohen, B. I., et al. 2017. “Monte Carlo Calculation of Large and Small-Angle Electron Scattering in Air.” Journal of Computational Physics 349: 582—588. doi: 10.1016/j.jcp.2017.08.014.
Farmer, W. A., and A. Friedman. 2015. “Effect of Multiple Scattering on the Compton Recoil Current Generated in an EMP, Revisited.” IEEE Transactions on Nuclear Science 62: 1695.
Farmer, W. A., et al. 2016. “On the Validity of Certain Approximations Used in the Modeling of Nuclear EMP.” IEEE Transactions on Nuclear Science 63: 1259. LLNL-JRNL-678008.
Friedman. A., et al. 2014. “Computational Methods in the Warp Code Framework for Kinetic Simulations of Particle Beams and Plasmas.” IEEE Transactions on Plasma Science 42(5): 1321.
——— 2016. “Studies of EMP Generation Using a Liénard–Wiechert Formulation, and ProgressToward a 3-D EMP Code.” Journal of Radiation Effects, Research & Engineering 34(1): 74—82. LLNL-JRNL-673748.
——— 2017. “EMPulse, a New 3-D Simulation Code for EMP Formation and Propagation.” Journal of Radiation Effects, Research & Engineering 35(1): 175—184. LLNL-JRNL-692743.
Goudsmit, S. and J. L. Saunderson. 1940. “Multiple Scattering of Electrons.” Physical Review 57(1): 24.
Grote, D. P., et al. 2005. “The Warp Code: Modeling High Intensity Ion Beams.” AIP Conference Proceedings 749(1) 55—58. doi: 10.1063/1.1893366.
Hanson, A. O., et al. 1951. “Measurement of Multiple Scattering of 15.7-MeV Electrons.” Physical Review 84(4): 634.
Higginson, D. P., 2017. “A Full-Angle Monte Carlo Scattering Technique Including Cumulative and Single-Event Rutherford Scattering in Plasmas.” Journal of Computational Physics 349: 589—603.
Jackson, J. D., 1999. "Classical Electrodynamics." New York, John Wiley & Sons.
Karkkainen, M., et al. 2006. "Low-Dispersion Wake Field Calculation Tools." Proceedings of the 2006 International Computational Accelerator Physics Conference, Chamonix, France, 35—40.
Karzas, W. J., and R. Latter. 1965. "Detection of the Electromagnetic Radiation from Nuclear Explosions in Space." Physical Review 137(5B): B1369.
Moliere, G. 1947. “Theorie Der Streuung Schneller Geladener Teilchen i. Einzelstreuung am Abgeschirmten Coulomb-Feld.” Zeitschrift für Naturforschung A 2(3): 133—145.
Longley, H. J., and C. L. Longmire. 1972. “Development of the CHAP EMP Code.” Defense Nuclear Agency Report DNA-3150T.
Longmire, C. L. 1978. “On the Electromagnetic Pulse Produced by Nuclear Explosions.” IEEE Transactions on Electromagnetic Compatibility 20(1): 3—13. doi: 10.1109/TEMC.1978.303688.
——— 1983. “The Early-Time EMP from High-Altitude Nuclear Explosions.” Mission Research Corporation Report MRC-R-809, prepared for LLNL.
——— 1985. “EMP on Honolulu from the Starfish Event.” Mission Research Corporation Theoretical Note 353.
——— 1986. “Justification and Verification of High-Altitude EMP Theory, Part I." Contract LLNL-9323905, Mission Research Report Theoretical Note 368.
Page, W. E., et al. 1975. “A Description of the HEMP-B Computer Code.” Air Force Weapons Laboratory Report AFWL-TR-73-286.
Schaeffer, N. 2013. “Efficient Spherical Harmonic Transforms Aimed at Pseudospectral Numerical Simulations.” Geochemistry, Geophysics, Geosystems 14(3): 751—758.
Vay, J. -L., et al. 2012. “Novel Methods in the Particle-in-Cell Accelerator Code-Framework Warp.” Computational Science and Discovery 5(1): 014019. doi: 10.1088/1749-4699/5/1/014019.
Publications and Presentations
Cohen. B, et al., 2016. “EMPulse, a New 3-D Simulation Code for Electromagnetic Pulse Studies.” 58th Annual Meeting of the APS Division of Plasma Physics, San Jose, CA, October 31—November 4, 2016. LLNL-ABS-696908.
Farmer. W., et al. 2016a. “Assessing the Validity of Common Approximations Used in Modeling Nuclear EMP.” 33rd Annual Hardened Electronics and Radiation Technology (HEART) Technical Interchange, Monterey, CA, April 4—8, 2016. LLNL-PRES-683958.
——— 2016b. “PIC Simulation of Nuclear Electromagnetic Pulse (EMP).” 46th Annual Anomalous Absorption Conference, Old Saybrook, CT, May 1—6, 2016. LLNL-ABS-684263 / Presentation: LLNL-PRES-690297.
Friedman, A., et al. 2015. “Studies of EMP Generation Using a Lienard-Wiechert Formulation, and Progress Toward a 3-D EMP Code.” Journal of Radiation Effects Research and Engineering (JRERE) 34, Number 1 (2016): 75—82. LLNL-JRNL-673748.
——— 2016a. “EMPulse, a New 3-D Simulation Code for EMP Formation and Propagation.” 33rd Annual Hardened Electronics and Radiation Technology (HEART) Conference, Monterey, CA, April 4—8, 2016. LLNL-CONF-677133.
——— 2016b. “Approaches to Simulating the Prompt Electromagnetic Pulse.” 58th Annual Meeting of the APS Division of Plasma Physics, San Jose, CA, October 31-November 4, 2016. LLNL-ABS-696910.
——— 2017a. “EMPulse, a New 3-D Simulation Code for EMP Formation and Propagation.” Journal of Radiation Effects, Research & Engineering (JRERE) 35: 175—184. LLNL-JRNL-692743.
——— 2017b. “3-D Simulation Codes for EMP E1 Formation and Propagation." Journal of Radiation Effects Research and Engineering (JRERE) 36. LLNL-JRNL-732043.
——— 2017c. “3-D Simulation Codes for EMP E1 Formation and Propagation.” 34th Annual Hardened Electronics and Radiation Technology (HEART) Technical Interchange, Denver, CO, April 24—28, 2017. LLNL-CONF-702578.
——— 2017d. “Simulating the Prompt Electromagnetic Pulse in 3D Using Vector Spherical Harmonics.” 59th Annual Meeting of the APS Division of Plasma Physics, Milwaukee, WI, October 23—27, 2017. LLNL-ABS-734577.