Jacob Schroder (14-ERD-013)
Abstract
Growth in high-performance computing will come from more central processing unit cores, not faster clock speeds. Previously, faster clock speeds decreased the compute time per time step, and thus allowed for more time steps while not increasing the overall compute time. However, clock speeds are no longer increasing, which will inevitably lead to increases in compute time. We plan to develop an algorithm to compute multiple time steps simultaneously in parallel, and thus accelerate time-stepping methods and provide a solution to the time-integration bottleneck. We will apply this algorithm iteratively and with scalability using multigrid methods, targeting hyperbolic and parabolic equations. Hyperbolic equations usually support solutions with discontinuities, such as a shock wave, whereas parabolic equations are found in time-dependent diffusion problems. Multigrid computation achieves its efficiency by applying two complementary processes, smoothing and coarse-grid correction, over successively coarser grids for a given problem. We expect to develop a nonintrusive multilevel algorithm that uses successively coarser time scales to accelerate the solution at the original fine-time scale.
By computing multiple time steps in parallel, we expect our algorithm to expose new parallelism in the time dimension and has the potential to dramatically decrease the overall time to solution for time-stepping methods and to allow for greater machine utilization on future computer architectures. Most current methods such as the parallel-in-time algorithm and its variants for solution of the general nonlinear system of ordinary differential equations are only two-level methods, and hence exhibit limited concurrency. We will develop new scalable, multigrid techniques for parallel time integration. While multilevel parallel-in-time methods may seem improbable, preliminary proof-of-concept results using the MATLAB computing language for algorithm development already shows optimal results for parabolic problems using implicit or explicit schemes.
Mission Relevance
Our planned algorithm to expose new parallelism in the time dimension will allow Laboratory codes to run faster and to better take advantage of the huge increase in concurrency coming with exascale computing, and supports the high-performance computing, simulation, and data science core competency, along with several LLNL mission areas that depend on these computing resources. Essentially, all Livermore production multiphysics codes make use of explicit time stepping, and are therefore subject to the serial time-integration bottleneck. The need for parallel time integration is imminent, and developing this technology and associated expertise helps the Laboratory maintain its leadership in high-performance computing ecosystems.
FY15 Accomplishments and Results
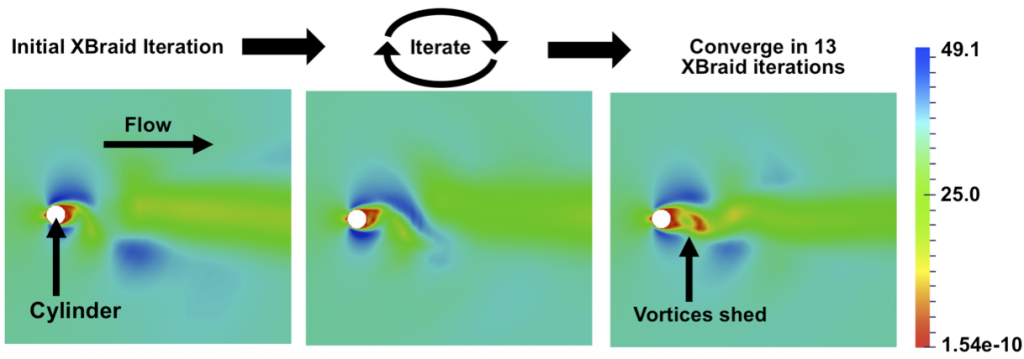
In FY15 we (1) focused on hyperbolic problems and explicit time-integration schemes, starting with linear advection in one dimension, which provides a simple problem to explore possible methods for more-complicated hyperbolic problems; (2) learned that some artificial dissipation is needed for the current method through theoretical investigation and experiments with the simpler, but similar, problem of the heat equation running near the stability limit; (3) examined the effect of shock waves on coarse timescales, starting with nonlinear advection (Burger's equation for modeling of gas dynamics and traffic flow); (4) released our parallel-in-time software framework XBraid code (with ~50 downloads from ~10 countries); (5) continued work on parabolic problems, focusing on scalability for nonlinear diffusion; and (6) continued to develop theory for heat and advection equations.
Publications and Presentations
- Schroder, J., "Parallel time integration with multigrid." SIAM J. Sci. Comput. 36, C635-C661 (2014). http://dx.doi.org/10.1137/130944230