Xiao Chen | 16-ERD-023
Overview
The overall goal of this project was to develop a new capability for large-scale source inversion of high-dimensional stochastic models, which is a crucial task performed within many applications at Lawrence Livermore National Laboratory. The purpose of the stochastic source inversion is to infer the optimal characterization based on stochastic simulations and measurements with uncertainties (e.g., noisy full-waveform seismic data), given an initial characterization (the prior information or estimation) of the stochastic source (a random field, such as earth structure in seismic inversion). Current stochastic source-inversion algorithms are deficient because their linearity, normal distribution, and inability to account for model uncertainties may adversely affect the integrity of the solution. The scope of our project included developing methods for (1) handling high-dimensional, non-Gaussian, and nonlinearly correlated stochastic sources; (2) propagating uncertainties forward through the stochastic models; and (3) propagating uncertainties backward via fast Bayesian inversion algorithms. We developed integrated software framework to manage the algorithmic complexity and uncertainty propagation, and we demonstrated this capability on selected test problems relevant to Laboratory missions. The goal in developing the software was to achieve efficient and robust high-dimensional source inversion, which will enable faster and more credible decision making for the Laboratory’s applications.
Background and Research Objectives
Computational science and engineering have enabled researchers to model complex physical processes in many disciplines, such as climate projection, subsurface flow and reactive transport, seismic-wave propagation, and power-grid planning. However, uncertainty in the model parameters makes the underlying problems essentially stochastic (i.e., randomly determined) in nature. Applying uncertainty quantification (UQ) to improve model predictability usually requires solving an inverse problem (inverse UQ) by fusing prior knowledge, simulations, and experimental observations. A state-of-the-art approach to inversion is the variational data assimilation method, which is analogous to the deterministic nonlinear least-square methods. However, this method by its deterministic nature cannot produce solutions with full descriptions of their probabilistic density functions (PDFs).
Alternatively, Bayesian inference provides a systematic framework for integrating prior knowledge (of the stochastic sources) and measurement uncertainties to compute detailed posteriors (Tarantola 2005). However, Bayesian inference of high-dimensional and nonlinearly correlated stochastic source is computationally intractable (Martin et al., 2012, Constantine 2015). Moreover, unreasonable choices of source priors may have major effects on posterior inferences. Other state-of-the-art inversion algorithms are limited in their applications because they often assume Gaussian priors and posteriors, linearly correlated source fields, and no parametric and model form uncertainties in the simulation models. These deficiencies may result in unreliable solutions, which may impact the credibility of decision making.
We developed an efficient and robust capability to make informed inferences about large-scale, complex, and uncertain systems, which will enhance current Laboratory applications for future contracts in areas of underground nuclear test detection and monitoring, oil and geothermal recovery, subsurface processes for CO 2 sequestration, radioactive waste deposition and noble gas detection, seismic inversion, wind and solar forecasting, and power grid management.
For example, in underground nuclear test detection, the objective is to identify a detonation location within the medium of rock with different physical properties using computational models and measurement data. Solving these stochastic inversion problems is challenging because the stochastic sources are often high-dimensional (thousands to millions) spatial-temporal random fields with nonlinear correlations and non-Gaussian distributions, the computational models are often plagued with many sources of uncertainty, the source inversion task can be computationally intensive, and measurement data may be sparse and noisy.
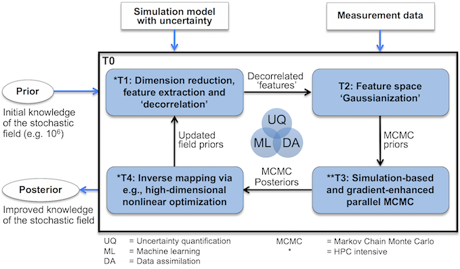
To address these deficiencies, we developed a new stochastic source-inversion software framework for handling high-dimensional, nonlinearly correlated sources with non-standard probability distributions, as well as for managing uncertainties in simulation models and measurement data (see figure). This framework, known as Data Assimilation for Stochastic Source Inversion (DASSI), contains efficient and robust methods for (1) the nonlinear dimension reduction of high-dimensional, non-standard, and nonlinearly correlated stochastic sources; (2) fast forward uncertainty propagation through ensemble model simulations; (3) backward uncertainty propagation via fast adjoint-based Bayesian inversion algorithms; and (4) high-dimensional source recovery via nonlinear optimization.
Impact on Mission
Our mathematical framework and the associated software platform have enabled several important Laboratory applications to more efficiently and robustly address their stochastic source-inversion problems and manage uncertainties. With this platform, practitioners and researchers now have a tool to identify any potential risk of a complex stochastic simulation based on measurements data that cannot presently be fully evaluated. The project has expanded the envelope of uncertainty quantification and stochastic data-assimilation methods to handle more general and complex scenarios. The software package will be made available to the wider scientific community for use and for further collaborative development.
Our project supports the NNSA goal of advancing the science, technology, and engineering capabilities that are the foundation of the NNSA mission. It also aligns with the Laboratory's core competencies in high-performance computing, simulation, and data science, and that of earth and atmospheric science.
Conclusion
We developed the DASSI software application that enables large-scale source inversion on high-performance computing systems, such as those at Lawrence Livermore National Laboratory. We used linear/kernel principal component analysis in the DASSI application to detect a linear manifold in the original space and in the transformed space, respectively. In the future, we will apply a deep auto encoder, which is an unsupervised deep-learning technique coupled with kernel-based methods.
References
Constantine, P. G. 2015. "Active Subspaces: Emerging Ideas for Dimension Reduction in Parameter Studies." Active Subspaces: Emerging Ideas for Dimension Reduction in Parameter Studies. doi: 10.1137/1.9781611973860.
Martin, J., et al. 2012. "A Stochastic Newton MCMC Method for Large-Scale Statistical Inverse Problems with Application to Seismic Inversion." Society for Industrial and Applied Mathematics Journal on Scientific Computation . Society for Applied Mathematics. 34(3): 1460–1487. doi: 10.1137/110845598.
Tarantola, A. 2005. "Inverse Problem Theory and Methods for Model Parameter Estimation." Society for Industrial and Applied Mathematics, Philadelphia, PA. doi: 10.1137/1.9780898717921.
Publications and Presentations
Thimmisetty, C. A., et al. 2017. "High-Dimensional Intrinsic Interpolation Using Gaussian Process Regression and Diffusion Maps." Mathematical Geosciences 50(1). doi: 10.1007/s11004-017-9705-y. LLNL-JRNL-728760.