Xiao Chen (16-ERD-023)
Project Description
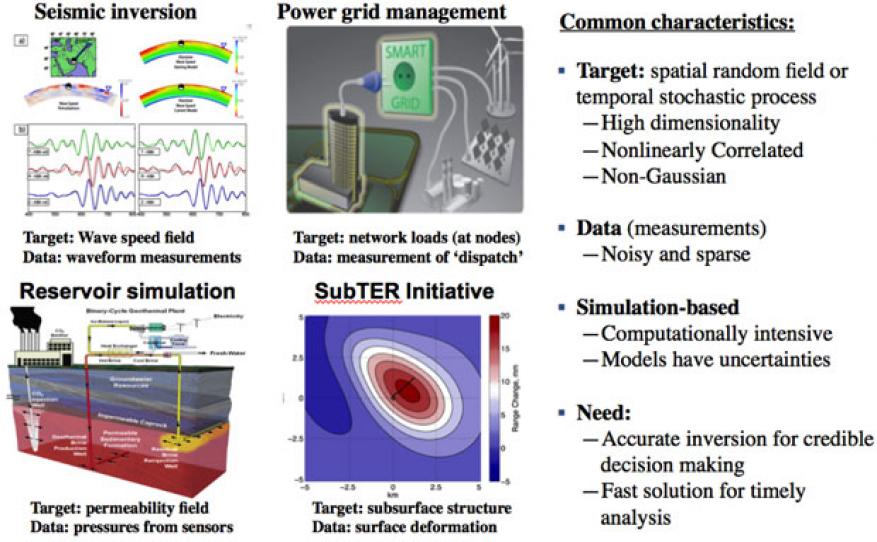
Many important, real-life applications face the need to conduct source inversion—that is, recovering the true characterization of an unknown source field from noisy measurement data and computer simulations of the underlying physical processes. For example, accurate characterization of the Earth's structure using seismic data is important for reliable nuclear explosion monitoring and ground motion hazard and assessment. In power-grid management, accurate representation of the state of the coupled distribution and transmission network (the source) is important for enhancing control strategies for fast-demand response, lower cost, higher efficiency, better reliability, and proactive vulnerability prevention. However, several challenges arise in a typical inversion process. First, the inversion may require tens of thousands of expensive model simulations. Second, the complex models may not accurately represent the underlying physical processes. Third, the measurement data, such as full waveform data in seismic monitoring or power output measurements in transmission line monitoring, may be sparse and polluted with random noises. In addition, the inversion algorithms currently available are limited in application because they suffer from intensive computational cost and assumption of a continuous probability distribution (Gaussian assumption), impacting the credibility of decision-making relevant to the applications. With this project, we plan to develop a high-performance-computing computational capability for large-scale source inversion of high-dimensional stochastic models (i.e. unpredictable systems with random variables). The scope includes high-dimensional data analysis, stochastic data assimilation, and nonlinear optimization. We will design efficient and robust algorithms for general and complex inversion and develop an integrated software framework to manage algorithmic complexity and model uncertainties. Finally, we will demonstrate our stochastic source-inversion capability on selected test problems relevant to Laboratory missions, such as seismic inversion, carbon dioxide sequestration, and power-grid management. The capability we develop will enable scientists to make precise statements about the degree of confidence they have in their simulation-based and data-driven predictions.
We expect to provide a mathematical framework and the associated software platform that will enable several important Laboratory applications to more efficiently and robustly address their stochastic source-inversion problems and manage uncertainties. The new platform will be free of Gaussian assumptions, resulting in more realistic data-driven probability distributions. Components of the platform include a forward-model framework using innovative goal-oriented stochastic reduction techniques for high-dimensional and nonlinear random-field representation and propagation. Additionally we will provide an efficient and robust inverse stochastic optimization and nonlinear optimization framework that can fully take advantage of parallel computing architectures. As a result of this platform's development, practitioners and researchers will have a tool to identify any potential risk of a complex stochastic simulation based on measurements data that cannot presently be fully evaluated. With respect to broader impact, this project contributes to advancing the envelope of uncertainty quantification and stochastic data-assimilation methods to handle more general and complex scenarios. The software package will be made available to the wider scientific community for use and for further collaborative development. Our research effort will also impact high-performance computing and simulation at Livermore by enhancing predictive simulations and providing a use case for exploring high-performance computer designs.
Mission Relevance
Our project aligns well with the Laboratory's core competency in high-performance computing, simulation, and data science, given that stochastic source inversion is a computationally intensive operation and thus requires extreme-scale computing capabilities. The work also enhances the strategic focus area of energy and climate security, because simulation-based inversion is of critical importance in subsurface technology and engineering research, seismic inversion, and power-grid management.
FY16 Accomplishments and Results
In FY16 we (1) implemented a kernel principle component analysis code in the C++ language that can handle Gaussian and polynomial kernels with higher orders, pre-imaging (mapping the feature random variables back to the random parameters) using fixed-point iteration, forward and reverse differentiation of the pre-imaging to compute the derivatives, and coupling of kernel principle component analysis and simulation-based and data-driven nonlinear optimal control; (2) added the adjoint capability to our in-house software "geocentric" to enable linear elasticity inversion; and (3) demonstrated that the derivative-based linear elasticity inversion has local convergence only, while our linear elasticity inversion based on principle component analysis has a global convergence with higher convergence rate if patterns are found in the parameters.
Publications and Presentations
- Chen, X., C. H. Tong, and J. White, Data assimilation and uncertainty management of large-dimensional dynamics models. SIAM Conf. Uncertainty Quantification, Lausanne, Switzerland, Apr. 5–8, 2016. LLNL-CONF-687597.
- Chen, X., et al., Goal-oriented nonlinear model reduction based on kernel principal component analysis for fast Bayesian inference. (2016.) LLNL-ABS-677841.