Scalable, Revealing Factorizations of Directed Graphs and Hypergraphs

Van Henson (13-ERD-072)

Abstract

There has been an explosion of interest and activity in recent years in data mining and graph analysis for large relational data sets, commonly modeled with extremely large, scale-free graphs and "hypergraphs," where entities (or properties) of one type are connected by an edge to several entities of differing type. These graphs are used to show hierarchies that may represent computer networks, communications, the Internet, social networks, power grids, and a host of other applications. The principal challenge arise in the sheer size of the matrices, because the graphs can become exceedingly large. These sizes have posed extremely difficult challenges in both computational and algorithmic scalability, which has restricted analysts to using very simple approximations, precluding the discovery of deeply significant but subtle relationships. In this project, we developed scalable multilevel factorizations for the deep analysis of data sets represented by nonsymmetric square and rectangular matrices, as well as new and effective affinity measures for partitioning, clustering, community identification, and topological analysis of data. These new methods build on our prior work in scalable eigensolvers (used to determine characteristic roots or values associated with a matrix equation) and multilevel methods to enable the deep analysis of complex data relationships. We delivered both theoretical advances and practical algorithms and codes to enable the analysis of diverse relational data at a scale not previously possible. Our new tools allow us to break the data sets into fundamental components that can be analyzed, filtered, and synthesized to highlight relevant connections. Moreover, the building blocks created in this project are applicable to a range of problems and applications of interest to graph theorists, data miners, bioinformatics researchers, and numerical analysts working on extremely large data sets.

Background and Research Objectives

The recent explosion of research activity in data mining^1,2 has seen graphs utilized to represent computer networks, communications, the Internet, the Web, social networks, power grids, and many other applications. Graphs can be represented by several different square sparse matrices, and much graph analysis—such as clustering of vertices, discovery of communities, and ranking the importance of vertices—can be cast as linear algebra problems. Undirected graphs lead to symmetric matrices, enabling real-valued solutions to the linear algebra problems and providing useful theoretical properties and effective computational techniques. However, one principal challenge arises in the sheer size of the matrices because the graphs can become exceedingly large—tens of billions of vertices are no longer unusual. Such sizes pose difficulties in both computational and algorithmic scalability.

Many of the graphs are directed, however, and relationships among the entities represented by the vertices may be highly asymmetric. The computational and theoretic difficulties that arise in treating the nonsymmetric case are considerable—hence analysts often symmetrize the data with full understanding that this may severely distorts the results.

Moreover, many relationships are not well represented by simple graphs, where each edge connects two like entities, but rather by hypergraphs, where entities of one type are connected by an edge to several entities (or properties) of differing type. Hypergraphs can be represented by rectangular matrices, with each row (vertex) having entries in several columns (properties and features). As with the nonsymmetric case, the rectangular matrices vastly increase the difficulty of the computation and greatly complicate the theoretical analyses.

The original twin goals of this project were:

• Develop scalable multilevel factorizations for the deep analysis of data sets represented by nonsymmetric square and rectangular matrices.
• Develop new and effective affinity measures that can be used for partitioning, clustering, community identification, and topological analysis of data.

Along the way, we realized that achieving additional goals was desirable, and in some cases essential, to the project’s success. Specifically:

• Create and use revealing factorizations by extending the existing path-based, agglomeration, and spectral algorithms from undirected graphs to hypergraphs and directed graphs.
• Test the functionality and scalability of the new algorithms by creating a synthetic graph generator that would preserve community structure from an input graph. While certain well-known graph generators (RMAT and BTER) attempt to do so, they fail to preserve certain important statistical parameters.

Scientific Approach and Accomplishments

Many relational data sets concern connections between entities of differing types, collected into a rectangular data array whose rows represent records and columns represent features and the (i,j)^th entry represents, for example, the strength, frequency, or probability of record i having feature j. Such a matrix represents a hypergraph, which is a generalization of a graph in which a set of vertices (people, places, and things) are connected by "hyperedges" (sets of two or more vertices sharing a feature). For example, we may say that documents (vertices) are connected by a hyperedge if they have the same keyword.

Certain well-known tools, such as the singular-value decomposition or principal-component analysis, can be used to decompose rectangular data matrices into factorizations intended to reveal underlying structure,^3–5 much as eigenvalue decompositions are used for analysis of graph Laplacian or adjacency matrices. The singular-value decomposition factors a rectangular matrix B = USV^T, where U is square with orthogonal columns, V^T is square with orthogonal rows, and S is the size and shape of B (nonnegative), with non-zeros in the B rank-leading diagonal entries, and zero elsewhere. Like the eigenvalue decomposition, the singular vectors in U and V can be used for a host of data-mining tasks, such as clustering records, estimating distance between records, or finding records that most closely match a set of records. However, the singular-value decomposition is a general-purpose tool. To reveal structure we know little about often requires digging deep into the spectrum, meaning we must conduct our data searches in relatively high-dimensional embeddings, which poses significant scalability, computational, and interpretational challenges. This is the primary problem we sought to address with faster, more scalable, and robust methods based on lower-dimensional embeddings that would take advantage of underlying properties of the structures we sought to reveal in the data.

We investigated properties of the so-called "thin singular-value decomposition," in which we approximated the singular-value decomposition with only a select subset of the singular vectors.⁴ For undirected graphs, our team discovered that computing too many eigenpairs was counterproductive—the trick is to determine and compute the optimal approximation. A related important discovery made in our prior work was that commute time, a measure commonly used for clustering and community identification, overemphasized certain graph features and required a careful statistical correction to be useful. We expected that similar principles would hold for the thin singular-value decomposition, and began with detailed analysis of the nature of eigenvectors of scale-free graphs.^6–8 These studies led to useful insights for singular-value decomposition developments. However, as expected, ferreting out systematic mathematical relationships remains a stiff theoretical challenge.

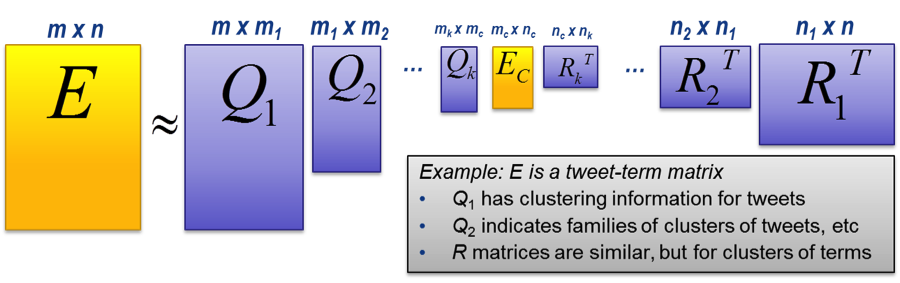
Hierarchical factorizations based on singular-value decomposition, conceptually illustrated in Figure 1, have proven to be a very useful notion. Figure 1 notionally shows a message-term matrix E for social-network tweets factored into matrices revealing broader (coarser, in multigrid lingo) groupings. The individual Q factors carry hierarchical grouping information that may define (at the various levels) responses, conversations, and topics, while R might make up clusters of terms, dialects, or social status of groups of tweeters. The depiction of groupings as coarse representations of the original fine-grained data is a natural extension of multigrid concepts.⁹

 

Figure 1. A notional display of a revealing factorization of the message-term matrix E for social tweets into hierarchical factors.

We vigorously pursued this line of inquiry, adapting multigrid approaches to specializations in graph and hypergraph analysis problems. It has proven very profitable, allowing us to develop fast multilevel co-clustering,¹⁰ adapt a Lean Algebraic Multigrid solver for use on scale-free graphs,¹¹ and develop support-graph pre-conditioners to accelerate the multigrid solvers.¹²

Clustering, partitioning, and community identification are most commonly done by selecting sets to globally maximize or minimize a desirable property, such as modularity or edge cuts.^13,14 An attractive alternative approach is to measure a distance, or affinity, between pairs of vertices and rank possible set-inclusions according to these distances. Commute time is a popular affinity measure.¹⁵ However, recent work has demonstrated that it is a flawed measure,¹⁶ being overly influenced by vertices that are highly central—that is, close to most of the graph. This reduces the effectiveness of commute time for clustering and partitioning applications. At the start of this project, we had discovered statistical corrections to commute time that facilitate its use in clustering and community identification for undirected graph problems. For highly directed and hypergraph problems, however, the answer is not so simple. Moreover, effective and efficient metrics are somewhat problematic when applied to large rectangular-data matrices. Hence, we set about developing a new affinity metric that could be generalized to the asymmetric and rectangular cases while including the best features of commute time (i.e., greater multiplicity of connecting paths between vertices increases their affinity) and avoiding the overemphasis of central vertices.

We investigated approaches based on decreasing affinity when the shortest connecting paths pass through many important (highly ranked) vertices, and basing affinity on weighted shortest paths by accounting for local structure encountered along the paths (e.g., the existence of short cycles involving edges along the path make the vertex pair closer together than paths without cycles). In the end, we defined a vertex affinity that quantifies the proximity between two vertices in terms of their clustering strengths, and devised a framework combining simple graph searches and resistance-circuit formulas to compute the affinity efficiently.¹⁷ We then proposed an edge-weighting scheme based on the vertex affinity measure and showed that the scheme can significantly improve the performance of community detection algorithms.¹⁸ We also devised a different approach to defining vertex closeness based on minimizing a certain nonlinear functional that is designed to expose when a vertex is closer to one of its neighbors than it is to the others. This scheme appears to be well defined for both directed and undirected graphs, and is efficiently minimized for bipartite graphs (a set of graph vertices decomposed into two disjoint sets such that no two graph vertices within the same set are adjacent).¹⁹

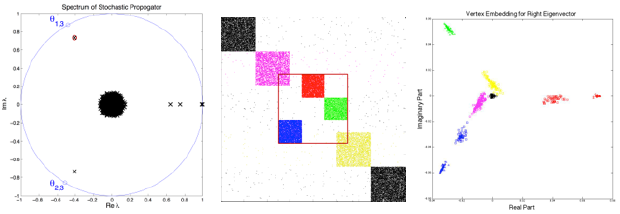
Two other notable achievements have resulted from this project. First, it is known that a highly cyclic substructure is an important feature in many types of complex networks, including the Web, protein–protein interaction, citation, and economic networks (see Figure 2). Bipartite (two cyclic) are the best known, but others (three cyclic) show up in a number of applications. Effective methods for finding such structures, especially when they are not “pure” and are hidden in the larger graph structure, have not previously been described. We have analyzed the nature of the complex spectrum and devised a method for identifying the presence of such substructures based on the nature of the complex eigenvalues of the graph matrix.²⁰ Once detected, the eigenvectors can be used to identify the vertices making up the substructure. Our work has shown that using the complex eigenvector allows detection of highly cyclic substructure with a single eigenvector, whereas the singular-value decomposition approach requires many eigenvectors, and its effectiveness in detecting highly cyclic structures is diluted by the presence of classical community structure. Our work, as far as we know, is the first use of complex-valued eigenpairs in graph clustering applications.

 

Figure 2. Our work shows that the spectrum of a graph containing a three-cyclic community will have points in the complex plane near the nontrivial third roots of unity, marked on the unit circle in the complex plane at θ_1,3 and θ_2,3 (left). The eigenvalues closer to one represent the other communities in the graph (noncyclic). A spy plot of the adjacency matrix of the graph is shown, center. The mostly solid squares on the diagonal (black, pink, and yellow) are conventional communities. The red, green, and blue squares represent a three-cyclic community embedded in the graph and overlapping the conventional communities. A two-dimensional embedding using the complex-valued eigenvector associated with θ_1,3 readily indicates the three-cyclic community structure (right).

Second, we developed a clustering graph generator that allows us to generate synthetic graphs based on the clustering behavior of a real input graph. The input graph is clustered, and the clusters, along with degree information, are passed to the graph generator, which creates a new and different graph preserving the community structure and degree information of the input model. This is a valuable tool for testing new graph analytics on synthetic, controlled graphs.²¹ To create a generator that preserved communities well, we performed an in-depth analysis of the properties of the Chung–Lu model, an important contemporary model of graph communities and one that is significantly more realistic than prior descriptions of community structure.²²

Impact on Mission

Conclusion

We have successfully devised multilevel graph and hypergraph factorization processes for the deep analysis of data for subtle or obscure structures. We also created a novel affinity measure and applied it to community detection schemes, thus accomplishing our two goals. In addition, we extended undirected graph analytics to directed graphs and hypergraphs, created a cluster-based graph generator, and discovered a technique for revealing regions containing highly cyclic substructure within a larger graph. We intend to pursue support to harden these prototypes into robust tools, and to employ the resulting tools on live sponsor-provided data.

References

1. Faloutsos, M., P. Faloutsos, and C. Faloutsos, “On power-law relationships of the Internet topology.” SIGCOMM. 29(4), 251 (1999).
2. Newman, M. E. J., “The structure and function of complex networks.” SIAM Rev. 45(2), 167 (2003). http://epubs.siam.org/doi/abs/10.1137/s003614450342480
3. Deerwester, S., et al., “Indexing by latent semantic analysis.” Am. Soc. Inform. Sci. 41(6), 391 (1990). http://onlinelibrary.wiley.com/doi/10.1002/%28SICI%291097-4571%28199009%2941:6%3C391::AID-ASI1%3E3.0.CO;2-9/abstract
4. Golub, G. H., and C. F. Van Loan, Matrix computations. The Johns Hopkins University Press, Baltimore, MD (1996).
5. Jolliffe, I., Principal component analysis. Springer-Verlag, Berlin, Germany (1986).
6. Sanders, G., and V. Henson, Eigenvectors of matrices associated with scale-free graphs. 16th Copper Mountain Conf. Multigrid Methods, Copper Mountain, CO, Mar. 17–22, 2013. LLNL-PRES-628160.
7. Sanders, G., et al., “Maximum principles and decay rates for extremal eigenpairs of scale-free adjacency and modularity matrices.” (2013). LLNL-JRNL-644341.
8. Sanders, G., et al., Numerical analysis of spectral embedding in graph mining applications. Conf. Statistical and Computational Challenges in Networks and Cybersecurity, Montreal, Canada, May 4–8, 2015. LLNL-PRES-670150.
9. Briggs, W. L., V. E. Henson, and S. F. McCormick. A Multigrid tutorial. Second edition. SIAM Press, Philadelphia, PA (2000).
10. Xu, H., H. De Sterck, and G. Sanders, Fast multilevel co-clustering: Unraveling the multilevel overlapping cluster structure of social network data. (2015). LLNL-CONF-665572.
11. Sanders, G., et al., An investigation into LAMG. (2015). LLNL-TR-678677.
12. Fox, A., et al., Support graph smoothing. SIAM Conf. Computational Science and Engineering, Salt Lake City, UT, Mar. 14–18, 2015. LLNL-PRES-668629.
13. Brandes, U., et al., “On modularity clustering.” IEEE Trans. Knowl. Data Eng. 20(2), 172 (2008). http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4358966&tag=1
14. Newman, M. E. J., “Fast algorithm for detecting community structure in networks.” Rev. E 69, 066133 (2004). http://journals.aps.org/pre/abstract/10.1103/PhysRevE.69.066133
15. Qiu, H., and E. R. Hancock, “Clustering and embedding using commute times.” IEEE Trans. Pattern Anal. Mach. Intell. 29(11), 1873 (2007). http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4302755
16. Von Luxburg, U., A. Radl, and M. Hein, “Hitting and commute times in large graphs are often misleading.” arXiv1003.1266v2 (2012). http://arxiv.org/abs/1003.1266
17. Yoo, A., et al., A novel vertex affinity for community detection. (2015). LLNL-TR-677840.
18. Yoo, A., et al., Enhancing community detection by affinity-based edge weighting scheme. (2015). LLNL-TR-677818.
19. Henson, V., et al., Assigning edge weights in graphs for quantifying vertex closeness. (2015). LLNL-JRNL-664198.
20. Klymko, C. F., Detecting highly-cyclic structure with complex eigenpairs. SIAM Conf. Computational Science and Engineering, Salt Lake City, UT, Mar. 14–18, 2015. LLNL-PRES-678196.
21. Winlaw, M., H. De Sterck, and G. Sanders, A clustering graph generator. (2015). LLNL-TR-678723.
22. Winlaw, M., H. De Sterck, and G. Sanders, An in-depth analysis of the Chung–Lu model. (2015). LLNL-TR-678729.

Publications and Presentations

• Boman, E. G., K. D. Devine, and S. Rajamanickam, “Scalable matrix computations on large scale-free graphs using 2D graph partitioning.” SC '13 Proc. Intl. Conf. High Performance Computing, Networking, Storage and Analysis. ACM, New York, NY (2013). LLNL-JRNL-645609.
• Breuer, A., G. Sanders, and A. Lumsdaine, Restarted minimal Krylov subspaces for low-rank approximation. (2013). LLNL-JRNL-643736.
• D’Ambra, P., and P. S. Vassilevski, Adaptive AMG with coarsening based on compatible weighted matching. (2015). LLNL-TR-613612.
• De Sterck, H., “Steepest descent preconditioning for nonlinear GMRES optimization.” Numer. Lin. Algebra Appl. 20, 453 (2013). LLNL-JRNL-645775. http://onlinelibrary.wiley.com/doi/10.1002/nla.1837/full
• De Sterck, H., and K. Miller, “An adaptive algebraic multigrid algorithm for low-rank canonical tensor decomposition.” SIAM J. Sci. Comput. 35, B1 (2013). LLNL-JRNL-645774. http://epubs.siam.org/doi/abs/10.1137/110855934
• De Sterck, H., and M. Winlaw, “A nonlinearly preconditioned conjugate gradient algorithm for rank-R canonical tensor approximation.” Numer. Lin. Algebra Appl. 22(3), 410 (2015). LLNL-JRNL-664163. http://onlinelibrary.wiley.com/doi/10.1002/nla.1963/full
• Fox, A., et al., Support graph smoothing. SIAM Conf. Computational Science and Engineering, Salt Lake City, UT, Mar. 14–18, 2015. LLNL-PRES-668629.
• Henson, V. E., et al., Assigning edge weights in graphs for quantifying vertex closeness. (2015). LLNL-JRNL-664198.
• Henson, V. E., et al., Computing edge weights for community detection through bipartite matching. (2014). LLNL-PRES-656212.
• Hu, H., H. De Sterck, and G. D. Sanders, Fast multilevel co-clustering: Unraveling the multilevel overlapping cluster structure of social network data. WSDM 15, 8th Intl. Conf. Web Search and Data Mining, Shanghai, China, Feb. 2–6, 2015. LLNL-CONF-657121.
• Jones, T., and G. Sanders, Aggressive coarsening strategies for numerical linear algebra on scale-free graph topology. SIAM Ann. Mtg, Chicago, IL, July 7–11, 2014. LLNL-PRES-657601.
• Klymko, C. F., Detecting highly cyclic structure with complex eigenpairs. SIAM Conf. Computational Science and Engineering, Salt Lake City, UT, Mar. 14–18, 2015. LLNL-PRES-678196.
• Klymko, C. F., and M. Benzi, A matrix analysis of different centrality measures. SIAM Ann. Mtg., Chicago, IL, July 7–11, 2014. LLNL-PRES-656617.
• Klymko, C. F., D. F. Gleich, and T. G. Kolda, Using triangles to improve community detection in directed networks. BigData/SocialCom/CyberSecurity Conf., Stanford, CA, May 27–31, 2014. LLNL-POST-656572.
• Ponce, C. V., and P. S. Vassilevski, Hierarchical graph Laplacian solvers for fast network simulation. (2014). LLNL-POST-658278.
• Sanders, G., Linear-algebraic graph mining. UCSF Medical School: New Applications of Computer Analysis to Biomedical Data Sets, San Francisco, CA, May 28, 2015. LLNL-PRES-671587.
• Sanders, G., and V. Henson, Eigenvectors of matrices associated with scale-free graphs. 16th Copper Mountain Conf. Multigrid Methods, Copper Mountain, CO, Mar. 17–22, 2013. LLNL-PRES-628160.
• Sanders, G., H. De Sterck, and H. Xu, Fast multilevel co-clustering: Unraveling the multilevel overlapping cluster structure of social network data. (2015). LLNL-CONF-665572.
• Sanders, G., L. Ward, and T. Jones, Numerical analysis of spectral clustering algorithms (SCAs). SIAM Ann. Mtg., Chicago, IL, July 7–11, 2014. LLNL-PRES-657600.
• Sanders, G., et al., An investigation into LAMG. (2015). LLNL-TR-678677.
• Sanders, G., et al., “Maximum principles and decay rates for extremal eigenpairs of scale-free adjacency and modularity matrices.” (2013). LLNL-JRNL-644341.
• Sanders, G., et al., Numerical analysis of spectral embedding in graph mining applications. Intl. Conf. Statistical and Computational Challenges in Networks and Cybersecurity, Montreal, Canada, May 4–8, 2015. LLNL-PRES-670150.
• Winlaw, M., H. De Sterck, and G. Sanders, A clustering graph generator. (2015). LLNL-TR-678723.
• Winlaw, M., H. De Sterck, and G. Sanders, An in-depth analysis of the Chung–Lu model. (2015). LLNL-TR-678729.
• Yoo, A., et al., A novel vertex affinity for community detection. (2015). LLNL-TR-677840.
• Yoo, A., et al., Enhancing community detection by affinity-based edge weighting scheme. (2015). LLNL-TR-677818.