Nils Petersson (16-ERD-018)
Project Description
For more than four decades, LLNL has been the world leader in the design, construction, activation, and operation of ever-more-complex high-energy Inertial Confinement Fusion laser drivers, culminating in the 192-beam National Ignition Facility. This dominant position has rested on the foundation of a unique capability to understand and numerically simulate the important physical processes that determine the success and failure of laser operation, which led to the ability to anticipate and avoid potential failure modes and to optimize cost and performance trade-offs. However, the cutting edge of new laser construction has now expanded into ultrashort-pulse lasers, an area in which the Laboratory has considerable expertise but has not kept pace regarding the capabilities needed to simulate their operation and thus optimize their design. We are attempting to close this gap in the area of ultra-intense, short-pulse lasers. One enabling technology for generating ultrashort laser pulses with sufficient energy to be of interest is chirped-pulse amplification, a method by which a spectrally dispersive element, such as a set of diffraction gratings (optical tools for reflecting light), is used to stretch an initial short pulse to nanosecond duration, allowing it to be amplified without damaging the amplifier. The high-energy pulse is then recompressed with another set of gratings. Approximations for modeling the grating compressor exist, but are not adequate to capture the effect of realistic diffraction gratings. We are developing a methodology for modeling the interaction of chirped-pulse-amplified laser beams with realistic diffraction gratings. This is challenging because of the enormous spatial and temporal difference in scale among the full-beam description, the time constant of the beam’s spectral content, and the spatial scale of the grating structure. We are combining LLNL’s expertise in laser modeling with expertise in multi-scale techniques, mathematical modeling, and high-performance computing to explore a number of approaches to this challenge.
We are developing advanced mathematical and computational techniques that will find application in multiple-wave propagation applications. We are addressing the issues of laser physics, mathematical methods, asymptotic analysis, computational efficiency and algorithm convergence, and high-performance computing with a multi-pronged approach to create an accurate simulation of the effect of realistic, imperfect grating stretchers and compressors on chirped-pulse-amplified laser beams. We are examining the application of boundary-element methods accelerated by the fast multipole method. This technique appears to naturally accommodate high-aspect-ratio spatial discretization, offering the prospect of enabling calculations in which grating lines are microscopically resolved in only one dimension while the longer-scale defects and line-direction anomalies are resolved on the millimeter scales that are natural to their rate of variation. We are also using the analytic results of modeling the wave-optics description of gratings, in which we derive a phase-transfer function that couples space and frequency. Our research will support the design of high-power, ultrashort pulse lasers at the Laboratory and will enable simulations to model how realistic gratings change the results of experiments. We expect to gain a detailed understanding of and the ability to simulate the spatial and temporal coupling introduced by various grating imperfections. By developing this capability, our research will advance the science of laser design. Simulation results will ideally be compared to other measured pulse shapes for ultrashort lasers at LLNL.
Mission Relevance
This project aligns with the lasers and optical science and technology core competency, which includes the general updating and modernization of laser simulation capability, specifically the development, design, and optimization of short-pulse lasers. It also supports the core competency in high-performance computing, simulation, and data science by fostering the development of advanced mathematical and high-performance computing techniques.
FY16 Accomplishments and Results
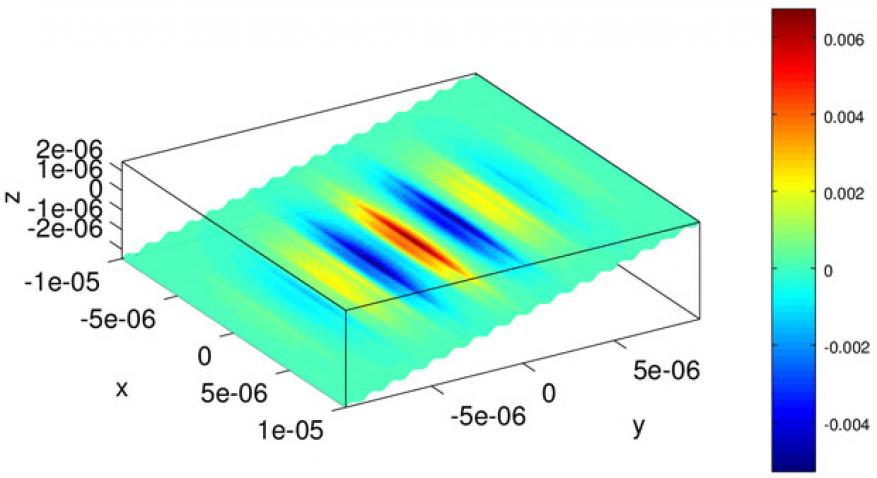
In FY16 we (1) modeled metallic diffraction grating in the frequency domain using a finite-element method to discretize the electric field integral equation governing the surface current along the grating (see figure); (2) tested a low-order method against analytical solutions for spherical surfaces, using a direct method; (3) discovered an unanticipated difficulty in which the condition number of the linear system grows rapidly with N (number of surface elements), hampering iterative methods, the mitigation for which involves a pre-conditioner based on Calderon’s identities discretized on a dual mesh, allowing iterative solution methods to converge quickly and independently of N; and (4) implemented the iterative solution method, first testing the Calderon pre-conditioner approach, and secondly, the fast multipole method.