Theoretical and Computational Studies of Rare Earth Substitutes: A Test Bed for Accelerated Materials Development

Lorin Benedict (13-ERD-044)

Abstract

Hard permanent magnets in wide use typically involve expensive rare earth elements. In this effort, we investigated candidate permanent magnet materials that contain no rare earths. Simultaneously, we explored improvements in theoretical methodology to enable better prediction of magnetic properties that are relevant for future design and optimization of permanent magnets. As part of this research project, we completed a detailed study of magneto-crystalline anisotropy energies and employed advanced simulation tools to better describe magnetic properties at elevated temperatures. In addition, our development of ab initio spin dynamics methods with this project will prove important in Lawrence Livermore's ongoing investigations of the dynamic properties of correlated materials. Finally, our work on shocked iron has important implications for a new phase-transformation kinetics effort at the Laboratory.

Background and Research Objectives

The price of rare earth elements, which are used in the manufacture of hard permanent magnets and phosphors, is rising dramatically, with China enjoying a near monopoly in production. Our search for substitutes for rare earth elements used a first-principles computational effort coupled with existing Laboratory experimental efforts on rare earth substitutes and a computational and statistical effort aimed at material properties optimization. We studied the figures of merit for candidate permanent magnets with both higher-fidelity/high-cost methods and lower-fidelity/low-cost methods. Magneto-crystalline anisotropy and temperature-dependent magnetic excitations were studied, setting the stage for eventual multiscale modeling of the coercivity (magnetic intensity) properties of materials.

Hard permanent magnets, or ferromagnets, that can perform useful work because of their propensity to resist the destruction or reorientation of their magnetic moments, are used widely in industrial applications such as electromagnetic motors in hybrid vehicles and wind turbines. These materials are often variants of Sm₂Co₁₇ (samarium-2–cobolt-17) or Nd₂Fe₁₄B (neodymium-2–iron-14–boron), both of which contain rare earth elements. Following DOE's critical materials strategy,¹ it has been recognized that less-expensive reduced rare earth materials or alternatives with no rare earths must be found to ensure our worldwide economic competitiveness. In the search for new hard permanent magnets, several figures of merit are known to be important, one of which is the magneto-crystalline anisotropy energy (MAE)—the energy to rotate the electron spins from easy- to hard-axis directions. A large MAE is desired if the material is to possess magnetic domains that resist reorientation when bathed in an external magnetic field emanating from a nearby magnet. Another property is the Curie temperature (T_C), or indeed any magnetic property at temperatures approaching T_C, because the operating temperatures of electromagnetic motors are typically well above room temperature. While theoretical and simulation techniques exist to predict these properties, true predictive capability is sorely lacking, due to the subtle dependence of these properties on the electronic structures of the complex materials involved. It was therefore our aim to survey these areas, while developing new prescriptions for the rapid and accurate computation of permanent magnet properties that may better enable the prediction of trends when composition and temperature are varied.

In the course of this research project, we conducted detailed ab initio theoretical investigations of the composition dependence of MAE for the rare-earth-free alloy of iron–cobolt–boron (Fe_1-xCo_x)₂B, explored the electronic structure and magnetic properties of so-called high-entropy alloys containing up to five elements, and studied various means of decomposing MAE into few-site contributions.^2–4 We also developed a new scheme to compute the temperature dependence of magnetic properties (such as MAE) in compounds with induced local moments. Finally, we studied two features of the interaction between magnetism and atomic structure: the temperature dependence of phase-transition kinetic barriers in uniaxially compressed iron, and the relationship between the MAE and a magneto-elastic high-spin to low-spin transition in YCo₅ (yttrium–cobalt-5)_.^5,6 While the results of some of these studies were inconclusive, this broad set of investigations allowed us to develop the necessary tools and understanding needed to support LLNL’s ongoing efforts in the area of critical materials research.

Scientific Approach and Accomplishments

Magneto-Crystalline Anisotropy Energy of (Fe_1-xCo_x)₂B

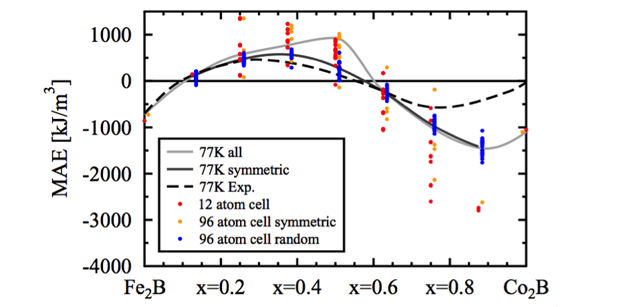
The MAE of a material is chiefly due to the interplay between the spin–orbit interaction, a consequence of the fact that electrons in high angular-momentum states orbit at relativistic speeds and the crystal-field effect that arises from the directional bonding in crystals. The smallness of the spin–orbit interaction, relative to typical chemical bond energies, renders the MAE difficult to calculate accurately. Moreover, materials with large magnetic moments and sizable MAEs are often those possessing narrowband electronic states that are notoriously difficult to treat within mean-field electronic structure theories. The alloy (Fe_1-xCo_x)₂B is a welcome counterexample in at least certain respects: no narrow f-band elements are present, and it is also the case that the MAE of this system is known experimentally throughout the entire range of cobalt compositions, thereby providing a test bed for ab initio theory. Using density functional theory, we computed MAE(x) using periodically repeated super-cells, and found trends that are similar to experimental results. Namely, the c-axis of this tetragonal material is the easy axis (favoring permanent magnet applications) for the (70%) iron-rich material, while the cobalt-rich side favors planar anisotropy. A major focus of our work was to investigate the effects on the MAE of both local lattice relaxations (shown to be small) and preferential ordering (shown to be more important on the cobalt-rich side). We also compared our results to those of other theoretical treatments of alloy disorder such as the coherent potential approximation, in which a multiple-scattering theory is used to model statistically uncorrelated cobalt–iron disorder. Figure 1 shows a series of calculations of MAE for (Fe_1-xCo_x)₂B for different super-cell sizes; the dependence of the MAE on cell size was shown to be particularly large on the cobalt-rich side.

Figure 1. Density functional theory results for the magneto-crystalline anisotropy (MAE) energy of (Fe_1-xCo_x)₂B as a function of cobalt concentration x.

Electronic Structure of High-Entropy Alloys

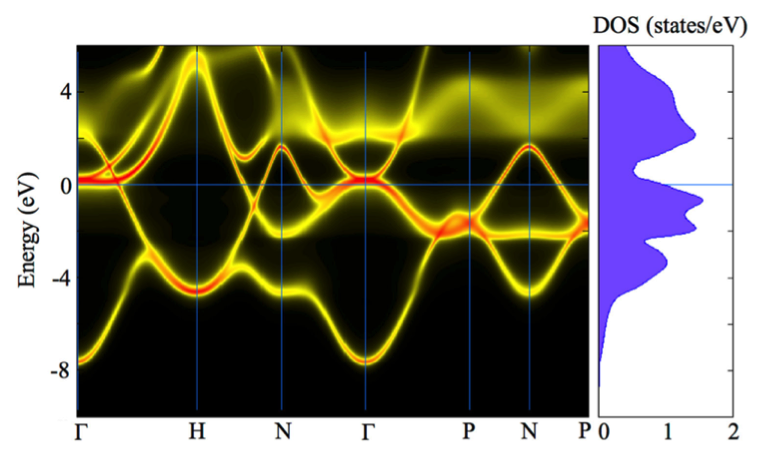
In many applications, the coherent potential approximation is the method of choice for the prediction of alloy electronic structure and associated magnetic properties. State-of-the-art Green's function Korringa–Kohn–Rostoker density functional theory codes using the coherent potential approximation allow for rapid prediction of properties for complex multicomponent systems. Because the search for rare-earth-free materials with favorable properties is likely to involve a comprehensive examination of such alloys, we participated in a joint study with Oak Ridge National Laboratory to better understand the stability and properties of so-called high-entropy alloys containing more than four elements. Figure 2 shows an example of an alloy electron spectral function for the five-component system molybdenum–niobium–tantalum–vanadium–tungsten.³ Local magnetic moments were also predicted, and comparisons were once again made to super-cell calculations, resulting in increased confidence in high-throughput calculation schemes for certain properties.

Figure 2. Alloy band structure (electron spectral function) for the alloy molybdenum–niobium–tantalum–vanadium–tungsten in its body-centered cubic phase as computed by the coherent potential approximation using density functional theory. Density of states (DOS) in number of states per electron volt (eV) energy is shown on the right.

Atom-Resolved Decompositions of the Magneto-Crystalline Anisotropy Energy

It is natural to presume that certain ions in a crystal lattice may contribute more to the MAE than others, or that certain ions may favor uniaxial MAE and others favor planar MAE. As such, we investigated various schemes to decompose the MAE into one-site and multi-site contributions, in an effort to aid the search for materials with favorable properties. The most sensible one-site decomposition proved to be that arising from a lamda-integration scheme applied to the spin–orbit interaction, in which ground-state matrix elements of the spin–orbit operator are decomposed into individual ionic contributions (suggested by many researchers in the past). However the usefulness of this decomposition was found to be marginal, because of a fundamental lack of gauge invariance. Less sensible still was a decomposition of the MAE using projected single-particle densities of states.⁴ A cluster expansion of the MAE for (Fe_1-xCo_x)₂B was also attempted, enabling the description of two-ion contributions, but we found this to be of little practical use as well.

Monte-Carlo Importance Sampling Scheme

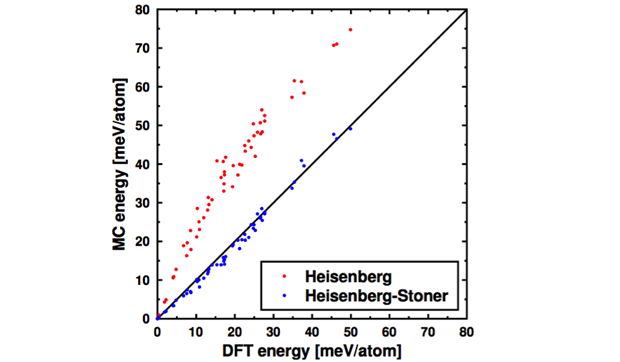
The importance of the temperature dependence of permanent magnet properties prompted us to study the ferromagnet CoPt (cobalt–platinum), at elevated temperature. Using density functional theory, we computed Heisenberg exchange parameters, J_Co–Co, J_Co–Pt, and J_Pt–Pt, and then compared the total energies of the associated Heisenberg model to those of density functional theory. Figure 3 shows the total energies for different spin configurations with the density functional theory versus Heisenberg model (red). The sizable discrepancy results from improper treatment of the platinum spin moments, and incorrect cobalt and platinum moment sizes for cases with locally misaligned spins (e.g., high-temperature configurations) in the Heisenberg model. Far better agreement is found with the more detailed Heisenberg–Stoner model, which includes the fact that the platinum moment is largely induced by the local magnetic field due to the neighboring cobalt spins (blue).⁷ With this improved agreement, it should be possible to perform Monte Carlo simulations of the temperature dependence of various magnetic properties, including MAE, with importance sampling in which the Heisenberg–Stoner model is used to sample the spin configurations, and the density functional theory is used more sparingly to evaluate spin–orbit and other energies not accessible to the model Hamiltonian. This would improve upon the simpler treatment of spin fluctuations adopted in the the disordered local moment approximation. Work along these lines continues.

Figure 3. Model Hamiltonian energies versus density functional theory energies for super-cells of the ferromagnet cobalt–platinum with spin configurations sampled from a range of temperatures.

Magnetic Structure of Uniaxially Compressed Iron

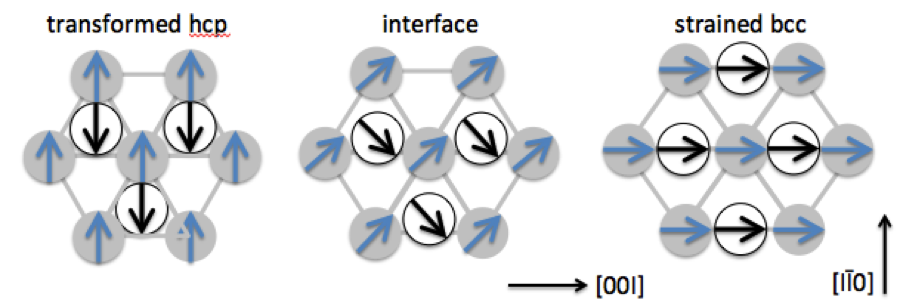
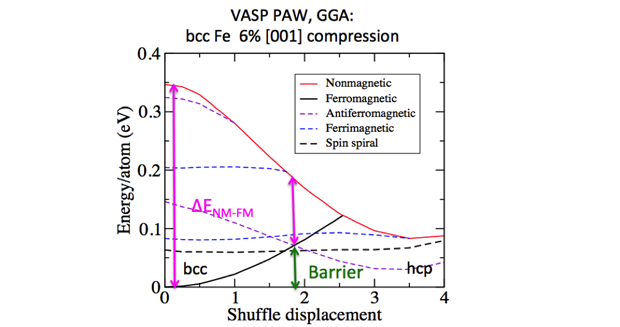
The often subtle interplay between magnetic properties and atomic structure is one of the many features of permanent magnet research that limits predictive capability. Indeed, predicting the energy (and free energy) differences between different magnetic configurations is difficult enough even for ions fixed in position. Decade-old work at LLNL on laser-shocked single-crystal iron⁸ provided us with the perfect opportunity to explore the role of spin fluctuations (i.e., magnons, a quasiparticle with a collective excitation of the electrons' spin structure in a crystal lattice) in the context of time-evolving ionic positions. We constructed generalized Heisenberg models for a range of intermediate crystal structures along the martensitic transformation path from ferromagnetic body-centered cubic iron to anti-ferromagnetic hexagonal closest-packed iron. Invoking an adiabatic hypothesis in which spin excitations are faster than ionic motion, we then used Monte Carlo with this family of spin-fluctuation Hamiltonians to predict the temperature-dependent transition barriers from body-centered cubic to hexagonal closest packed. Figure 4 shows a schematic representation of the transition, in which body-centered cubic iron is strained uniaxially along the [001] direction. Figure 5 shows our main result: spin-spiral and anti-ferromagnetic states have much smaller energy barriers than do other magnetic configurations, and Monte Carlo simulation results (not shown) suggest that the experimental findings can be explained by a significant lowering of the barrier from thermally excited magnons. Though iron is not a permanent magnet, this study opens the door to further work on the coupling of lattice distortions and magnons.⁵

Figure 4. Schematic representation of uniaxially compressed body-centered cubic (bcc) and hexagonal closest packed (hcp) iron.

Figure 5. Density functional theory results for the transition barrier between body-centered cubic (bcc) and hexagonal closest-packed (hcp) iron.

Investigation of Yttrium–Cobalt-5 Under Hydrostatic Stress

The alloy YCo₅, a non-rare-earth analogue of the rare earth magnet SmCo₅ (samarium–cobalt-5)_, which is a cousin to Sm₂Co₁₇, has a sizable MAE that is greatly underpredicted by standard density functional theory. It was shown 14 years ago that the addition of orbital polarization, a beyond-density-functional theory extension designed to encourage the satisfaction of Hund’s second rule, solves this problem.⁹ However, it is often the case that the more fashionable density functional theory +U is considered when standard density functional theory fails (the functional resulting from this combination of a local Hartree–Fock functional of a correlated subspace and a standard functional of the density or spin density is commonly referred to as a “+U” extension of density functional theory). We reinvestigated this problem with both density functional theory +U (with a value of U chosen to match the ambient-pressure MAE of YCo₅) and density functional theory with orbital polarization. We performed our calculations not only in ambient conditions, but also as a function of moderate hydrostatic stress, because YCo₅ is known to undergo a pressure-driven magneto-structural high-spin to low-spin transition.¹⁰ We found that density functional theory coupled with orbital polarization is indeed the more sensible tool to use, given that the measured high-spin to low-spin transition is pushed far too high in pressure if density functional theory +U with our optimized value of U is used instead.⁶

Impact on Mission

This project aligns with the DOE’s initiative focusing on the search for rare earth element substitutes and advanced the Laboratory’s strategic focus area of energy and climate as well as the core competencies in advanced materials and manufacturing and computational science and engineering. Our work strengthened LLNL’s activities for the Critical Materials Institute led by Ames National Laboratory in Ames, Iowa, particularly the magnetism thrust area, now entering its third year.

Conclusion

The area of permanent magnet research, particularly the search for rare-earth-free and rare-earth-reduced permanent magnets, is a challenging one. Our research into this field has produced promising new tools for us that are being applied both within and outside this immediate area. We expect that our developments in the Monte Carlo simulation of temperature-dependent magnetic properties will be important for future work within the Critical Materials Institute. Our continued development of ab initio spin dynamics methods, initiated here, will prove important in LLNL’s ongoing investigations of the dynamic properties of correlated materials. Our work on shocked iron has important implications for a new phase transformation kinetics effort at LLNL (in which two of our members have also become active participants). A postdoctoral researcher at LLNL, converted to full-time staff during this project, currently plays a crucial role in the critical materials effort.

References

1. Chu, S., Critical materials strategy. U.S. Department of Energy (2011).
2. Daene, M. et al., “Density functional theory calculations of magnetocrystalline anisotropy energies for (Fe_1-xCo_x)₂B.” J. Phys. Condens. Matter 27, 266002 (2015). LLNL-JRNL-668445. http://dx.doi.org/10.1088/0953-8984/27/26/266002
3. Troparevsky, M. C., et al., “Beyond atomic sizes and Hume-Rothery rules: Understanding and predicting high-entropy alloys.” J. Miner. Met. Mater. Soc. 67(10), 2350 (2015).
4. Aberg, D., B. Sadigh, and L. X. Benedict, On the site-decomposition of magnetocrystalline anisotropy energy using one-electron eigenstates. (2015). LLNL-TR-678619.
5. Surh, M. P., L. X. Benedict, and B. Sadigh, Magnetostructural transition kinetics in shocked iron. (2015).
6. Benedict, L. X., et al., Search for a consistent mean-field treatment of magnetic properties of YCo₅ under moderate hydrostatic stress. (2015). LLNL-TR-678582.
7. Polesya, S., et al., “Finite-temperature magnetism of Fe_xPd_1-x and Co_xPt_1-x alloys.” Phys. Rev. B 82, 214409 (2010).
8. Hawreliak, J. A., et al., “In situ x-ray diffraction measurements of the c/a ratio in the high-pressure ε-phase of shock-compressed polycrystalline iron.” Phys. Rev. Lett., 95, 075502 (2015).
9. Steinbeck, L., M. Richter, and H. Eschrig, “Itinerant-electron magnetocrystalline anisotropy energy of YCo₅ and related compounds.” Phys. Rev. B 63, 184431 (2001).
10. Rosner, H., et al., “Magneto-elastic lattice collapse in YCo₅.” Nat. Phys. 2, 469 (2006).

Publications and Presentations

• Aberg, D., B. Sadigh, and L. X. Benedict, “On the site-decomposition of magnetocrystalline anisotropy energy using one-electron eigenstates.” (2015). LLNL-TR-678619.
• Benedict, L. X., et al., Search for a consistent mean-field treatment of magnetic properties of YCo₅ under moderate hydrostatic stress. (2015). LLNL-TR-678582.
• Daene, M., et al., “Density functional theory calculations of magnetocrystalline anisotropy energies for (Fe_1-xCo_x)₂B.” J. Phys. Condens. Matter 27, 266002 (2015). LLNL-JRNL-668445. http://dx.doi.org/10.1088/0953-8984/27/26/266002