Nils Petersson | 16-ERD-018
Overview
We developed and implemented numerical techniques for three-dimensional high-performance computer simulations of laser grating compressors with imperfect metallic gratings. Our methodology enables detailed analysis of the effects of the line-scale grating perturbations to be analyzed in detail. First, the incident chirped (i.e., ultra-short) laser pulse is Fourier decomposed in time such that each frequency can be treated as a monochromatic laser beam. Each beam is propagated through the compressor by solving Maxwell's equations in the frequency domain. The incident electromagnetic field induces a surface current on the first grating, which, in turn, generates a diffracted field. We found that the physical optics approximation provides an efficient alternative to solving the electric field integral equation that governs the surface current. By introducing a simple scaling factor in the approximate surface current, we found that the diffracted electromagnetic fields become very accurate. The diffracted field from the first grating is the incident field for the second grating, and so on. The surface current on the last grating yields the compressed electric field and is evaluated on an observation plane. The calculations are repeated for each frequency, after which the electric field on the observation screen is inverse Fourier transformed to obtain the time-dependent electric field.
Even with the physical optics approximation, this calculation is daunting. About 10 billion point sources are needed to accurately represent the magnetic field radiated by the surface current on the undulating surface of a small grating. To accurately calculate the surface current on the subsequent grating, the magnetic field must be evaluated at about one billion locations along its surface.
This calculation is made tractable by applying an efficient multi-level directional Chebyshev interpolation technique, where the computational complexity is approximately linear in the sum of the number of point sources and evaluation locations. The technique is implemented for parallel computing based on the message passing interface library. We demonstrated our approach by simulating the compression of a chirped laser pulse through a small compressor with imperfect gratings.
Background and Research Objectives
Chirped pulse amplification, originally proposed by Strickland and Mourou (1985), is a crucial enabling technology for creating very short laser pulses with very high peak power. Conceptually, it consists of three optical components: a stretcher, an amplifier, and a compressor. Both the stretcher and the compressor rely on the fact that a short laser pulse contains a broad spectrum of frequencies, where each frequency corresponds to a monochromatic (i.e., single wavelength) laser beam. A laser pulse of short duration can therefore be analyzed as a sum of laser beams, where the amplitude and phase of each beam depend on the frequency. An initial laser pulse of very short duration and low energy content is first extended in time by the stretcher. The resulting pulse becomes chirped in time, which means that the frequency varies monotonically with time (similar to a bird’s chirp). The stretched pulse has low energy content and very low peak power. It is then amplified to increase its energy content, ideally without changing its duration and chirp. The amplified pulse is finally shortened in time by "un-chirping" the pulse in the compressor, resulting in a laser pulse with very short duration and very high peak power.
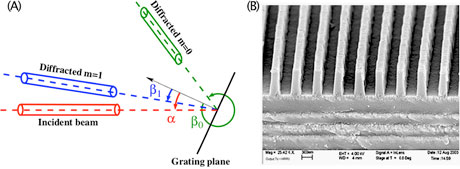
To explain how a laser pulse can be shortened in time, we must first consider how the incident monochromatic beam corresponding to each frequency propagates through the diffraction gratings in a compressor. A diffraction grating consists of a planar surface with parallel grooves where the spacing between the grooves is on the order of the wavelength of light (see figure).
Due to constructive and destructive interference, a grating diffracts monochromatic light in several discrete directions called orders . The grating in the figure allows only two orders, m = 0 and m = 1. The m = 0 order corresponds to specular diffraction, similar to a regular mirror. The m = 1 diffraction can be used for compression because its diffraction angle depends on the wavelength (and frequency) of the incident beam. This phenomenon is called angular dispersion (Diels and Rudolph 2006). For perfectly periodic gratings, angular dispersion is described by a simple trigonometric relation called the grating equation (Palmer and Loewen 2014). It relates the angle of diffraction to the angle of incidence and the ratio between the wavelength and the groove spacing. Due to the angular dispersion, the path length through the compressor depends on the frequency of the incident beam. By selecting the grating period carefully and positioning the individual gratings very precisely, it is possible to make all frequency components exit the compressor nearly simultaneously and in the same direction, thereby forming a laser pulse of very short duration and high peak power (Diels and Rudolph 2006).
Impact on Mission
This project has application to the NNSA's stockpile stewardship mission and enhances the Laboratory's core competencies in high-performance computing, simulation, and data science. Also, the development of an efficient directional Chebyshev interpolation algorithm for high-frequency electromagnetic wave propagation supports Lawrence Livermore National Laboratory's core competencies in lasers and optical science and technology. Finally, the implementation of the algorithm on distributed memory machines and the code developed during this project provide a new simulation capability for analyzing short-pulse lasers, which supports the Laboratory's research efforts in inertial confinement fusion science and technology.
Conclusion
The capabilities developed during this project could be extended to simulate much larger compressors with decimeter-sized gratings (Petersson et al. 2018). Further improvements of the code would be needed to simulate high compression ratios, which could require up to 10,000 frequencies to be calculated. Further optimizations of the code and faster hardware would enable such simulations to be performed within a few hours on a sufficiently large number of compute nodes.
References
Diels, J.-C. and W. Rudolph. 2016. Ultrashort Laser Pulse Phenomena. Academic Press. doi: 10.1016/B978-0-12-215493-5.X5000-9.
Palmer, C. and E. Loewen. 2014. Diffraction Grating Handbook, 7e. Newport Corporation, New York.
Petersson, N. A., et al. 2018. Numerical Simulations of Realistic Grating Compressors. Technical Report (74 pages). LLNL-TR-760459.
Strickland, D. and G. Mourou. 1985. "Compression of Amplified Chirped Optical Pulses." Optics Communications 55(3): 219–221. doi: 10.1016/0030-4018(85)90120-8.
Publications and Presentations
Petersson N. A., et al. 2018. "First Principles Modeling of Short Pulse Laser Grating Compressors Using High Performance Computing." Lawrence Livermore National Laboratory Computation Directorate External Review Committee Meeting. LLNL-POST-749230.
——— . 2018. Numerical Simulations of Realistic Grating Compressors. Technical Report. LLNL-TR-760459.
Sjogreen, B. and N. A. Petersson. 2018. "Numerical Simulation of Diffraction Gratings." SIAM Annual Meeting, Portland, OR, July 2018. LLNL-ABS-745544 and LLNL-PRES-754250.