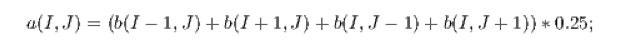Daniel Quinlan (16-FS-001)
Abstract
The universal number format and computation system (unum) allows a new approach to computer arithmetic, encompassing all floating-point formats (the formulaic representation that approximates a real number to support the trade-off between range and precision) as well as fixed-point and exact-integer arithmetic. Unums use a variable number of binary bits (depending on the number of digits required) for storing real numbers as binary bits in a computer. This new number type obtains more accurate answers than the IEEE 754 floating-point arithmetic standard established by the Institute of Electrical and Electronics Engineers, yet uses fewer bits in many cases, saving memory, bandwidth, energy, and power. The IEEE standard defines arithmetic and interchange formats, along with rounding rules, operations, and exception handling. With unums, we have the possibility to significantly change how we support floating-point within high-performance computing by providing greater precision, specific information about any imprecisions, and error-bound evaluation within applications running in a high-performance computing environment. The unum format lacked hardware support, as well as compiler and language support, and had not been used outside of example algorithms that demonstrate its novel features. Our project focused on evaluating the feasibility of the unum format for Livermore's high-performance computing environments and applications, specifically, evaluating a C/C++ implementation of Type 1 unums. We performed the study based on the Livermore Unstructured Lagrangian Explicit Shock Hydrodynamics (LULESH) proxy application, which is a shock hydrodynamics mini-application, by replacing all floating-point operations with unums. We determined the LULESH code was adapted to better utilize unum semantics, and we evaluated the impact on precision when using unums instead of IEEE floating-point types.
Background and Research Objectives
The IEEE 754 standard for floating-point arithmetic has existed for so long that it is not considered controversial, despite the numerous examples of acknowledged disadvantages of the rounding properties of today’s floating-point precision. Not since the development of the original floating-point number in 1914 has there been such an opportunity to so radically change the basis of high-performance computing as with unums. In 2015 John L. Gustafson published a new approach to computer arithmetic: the Universal Number (unum).1 This approach was called Type 1 unum, while Gustafson's ongoing work on an alternative unum representation is called Type 2. The unum encompasses all IEEE floating-point formats as well as fixed-point and exact integer arithmetic. It is a superset of IEEE 754 floating-point, with several advantages. Computing with unums provides more accurate answers without rounding errors, underflow, or overflow. Since operations with unums are associative, expressions can be evaluated in parallel for an increase in performance. Crafting a sequence of operations to minimize round-off error, as with IEEE floats, is no longer necessary.
In contrast to fixed-sized IEEE numbers, a variable number of bits can be used to encode numbers as unums. This allows numbers with only a few significant digits or with a small dynamic range to be represented more compactly. Numbers that require higher precision or range can expand as needed. Overall, using fewer bits for numbers can lead to lower memory usage and consequently lower energy consumption on an exascale machine by moving less data. Another unique feature of unums is the ability to represent intervals with open and closed endpoints. When a number cannot be represented exactly for a given precision, an interval is used to indicate the possible range of values. Calculations performed at lower precision will likely result in wider intervals, which indicates more uncertainty, but the answer will still be correct. When enough precision is available, operations with exact unums will produce exact results. Unum calculations are normally error-free; however, rounding can be applied explicitly to results with the guess function. Separation of the guess function from normal unum operations allows an application to control when rounding is appropriate. The guess function, when applied to a unum after an arithmetic operation, will produce a rounded result much like a floating-point calculation.
Currently no hardware support is available for unums; however, several software implementations are in active development. At least two implementations in the high-level dynamic programming language Julia and one in Python are publicly available on GitHub. Our Livermore version, developed as part of this project and implemented in C/C++, is functional and has been released as open source on Github (LLNL-CODE-704762). Andrew Klofas is working on a unum Type 2 library in C. Hence, there is a lot of ongoing work now on unums where various institutions provide their implementations for comparison. Even though the performance of these libraries will not rival a native hardware implementation, the performance is adequate for exploring the benefits of unums and tool interfaces.
Our goal for this project was to evaluate the use of unums by replacing float and double operations in the Livermore proxy application LULESH and to evaluate its impact on precision, accuracy, and the compression factor in comparison with the original IEEE float, double, and long-double computations.
Scientific Approach and Accomplishments
Since our goal was to evaluate unums for LULESH, we implemented Type 1 unums in a C library with a C++ wrapper. The C++ wrapper was then used to systematically replace all uses of float, double, and long-double, and compute statistics about memory consumption, precision, and accuracy. Among our accomplishments, we provided the first full implementation of Type 1 unums in C and published the implementation on Github. Based on this implementation we performed various evaluations with variants on how we introduced unum computations in LULESH. The results are promising, showing better precision with similar or less memory consumption for representation of floating-point numbers in several cases.
This section of our report includes the following sections:
- "Overview of Essential Properties of Unums" gives a short overview of the properties of unums.
- "Livermore's Unum Library (Implementation)" describes our implementation of the unum number representation in a Livermore library.
- "Evaluation with Livermore's LULESH Proxy Application" presents our evaluation results for three variants on how we introduced unums in the LULESH proxy application.
- "Indexing Support for Variable Length UNUM Representation" presents a conceptual overview of how unums with variable precision (and length) can be utilized in streaming operations in comparison to floating-point numbers of fixed size.
Overview of Essential Properties of Unums
The essential properties of unums are as follows:
- Variable precision and range with a new number format
- Format specifies exponent and fraction size
- Uncertainty (inexact) bit included in format (not as a central-processing-unit flag)
- Related: Arbitrary precision libraries
- Intervals with open or closed endpoints
- Can avoid rounding, underflow, and overflow errors
- Related: Interval libraries
Unums can produce true and useful statements without underflowing or overflowing. If the answer needs to be more precise, then more bits can be used, but even if the system’s limit is reached they never under- or overflow and mathematical operations can continue to produce useful results.
Instead of an underflow or overflow, an imprecision bit is set in the unum representation indicating that past a certain digit more than one value is represented by this unum. This converts a single (precise) number into an interval. Larger intervals, or intervals that do not fit exactly into the binary representation of a binary floating-point number up to a certain bit, are represented as so-called ubounds, which is a pair of unums, marking the beginning and end of an interval. Thus, unums are a specific encoding scheme of variable precision numbers with open and closed intervals. Instead of truncation or round-off, unum arithmetic establishes an interval representation (by using unums or ubounds) to bound the possible values in a computation. The correct, precise answer is always guaranteed to be inside the computed intervals. Conversely, no such guarantee can be provided with IEEE floating-point numbers. The variable precision of unums also allows the representation of exact numbers with less bits than a IEEE floating-point number. For example, 1.0 can be represented as 1 without storing all the additional 0s past the decimal point as is required for IEEE floating-point numbers.
Livermore's Unum Library (Implementation)
The unum library developed at Livermore supports variably sized unums, from a few bits up to thousands, and is designed with a modular structure to facilitate experimentation and use with compiler tools such as ROSE. Its design allows for the gathering of statistics and the tracking of unum precision throughout application runs. Unum precision can be changed at run time for different application subtasks through calls to a unum environment function. The maximum number of bits for the exponent and fraction are specified independently.
Functions are available that convert between unums and primitive "C" types such as integers and floating-point numbers. The relational operators, four arithmetic operators (add, subtract, multiply, and divide), and square root are also implemented. Additional relational operations are available to detect when unum intervals overlap or are completely disjointed. Unum print functions will display values in interval notation. Transcendental, complex, and fused operations have not been implemented yet. The three main interfaces to unum functionality (listed below) are available in the source directory:
- unumxx.h: C++ wrapper class that allows unums to be used with the standard arithmetic operators
- unum.h: C function interface that stores unums in a variable length byte array
- hubnd.h: C function interface that stores unums in a data structure
The implementation is written in C and is patterned after the Mathematica prototype code; function names are also the same as those in the Mathematica implementation.1 The unum library uses the GNU Multiple Precision Arithmetic Library for the low-level arithmetic.2 This arithmetic library must be installed on the machine to build and use the unum library. Cross-platform support for the library is provided with the GNU autotools build system.
Operations on unums through the library are several thousand times slower than operations on IEEE standard types with floating-point hardware. While faster implementations of the library are possible, the intent of this implementation is to provide flexibility for research purposes and accurate results.
Evaluation with Livermore's LULESH Proxy Application
Overview
LULESH describes the motion of materials relative to each other when subject to forces, and it also partitions the spatial problem domain into a collection of volumetric elements defined by a mesh.
Code Adaptions of LULESH and Running LULESH with Unums
We have adapted LULESH such that it can be run with unums instead of using float or double point numbers. We ran LULESH in three modes, each one utilizing unums with different trade offs:
- Round (guess) after each operation: No intervals. Our evaluation appears in the section "Livermore Unum Library (Implementation)."
- Round (guess) on each assignment: Expressions are calculated with intervals and only the result is rounded when assigned to a variable. Our evaluation appears in this section, below.
- Round (guess) select expressions: Only time and volume expressions are rounded, all others are calculated with intervals. Our evaluation appears in the section "Indexing Support for Variable Length UNUM Representation."
These variants are possible because we applied several modifications to LULESH. Below, we describe the modifications and provide the evaluation results.
Modifications Made to LULESH and Evaluated Variants
Getting LULESH to run in the first two modes was simple and required very little modification to the source code. A typedef (a special code command) was used to specify that the ubound class should be used to represent reals. To avoid converting real literals to a double first and then to unums, all real literals were wrapped by the RLIT macro, allowing unums with more precision than a double to be initialized to their full precision.
- Use ubound class to represent reals
- typedef ubnd˙c Real˙t; // floating-point representation
- Use macro to specify real literals with a string
- #define RLIT(arg) Real˙t(#arg)
- Avoid converting to double first
The third mode, running LULESH with intervals, required more effort and was met with several challenges.
Interval arithmetic in general has trouble with disjoint sets after a divide operation containing zero. The Boost implementation returns two intervals. Unum division returns a NaN (a "not a number," which is a numeric data type value representing an undefined or unrepresentable value) when the divisor is an interval containing zero. This result is also inconsistent with IEEE floating-point behavior which returns infinity if the dividend is non-zero. Changes to the program code are necessary to guard against intervals containing zero. With a smaller fraction size, intervals expand more with each operation leading to an extreme value. These extreme values eventually lead to LULESH internal errors that result in program termination at self-checks (negative volume or excessive artificial viscosity errors). Inserting guess calls around time and volume expressions helped to reduce abnormal termination conditions.
Using interval arithmetic leads to more complexity in program flow. A comparison of two unum intervals can result in any of 18 possible conditions of overlap. Effort is required to interpret all conditionals involving reals with respect to intervals. Most of the cases in LULESH were easily resolved since they were simply clipping a variable to a low or high limit. Clipping functions were introduced in place of the explicit code. For the other cases, we used an endpoint comparison function. This function includes an extra argument for each interval that specifies which endpoint (i.e., left or right) will be compared. The result is an integer that is less than, equal to, or greater than zero.
- Time step
- Time values are exact
- Use guess function on time and delta time values
- Better to take the minimum of delta time
- Divide by zero
- δx = (xt2 - xt1) may result in interval containing zero
- Add a small value "ptiny" to make non-zero
- Use guess function to collapse interval
- Negative volume internal self-check
- Use guess function on volume variables
- Clipping, maximum and minimum
- clipl(arg, limit) and cliph(arg, limit)
- Comparisons, specify lower or upper endpoint
- cmpe(arg1, ep1, arg2, ep2) returns -1, 0, +1
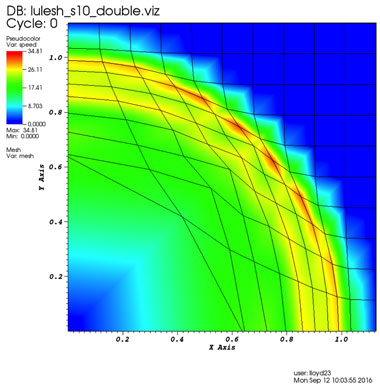
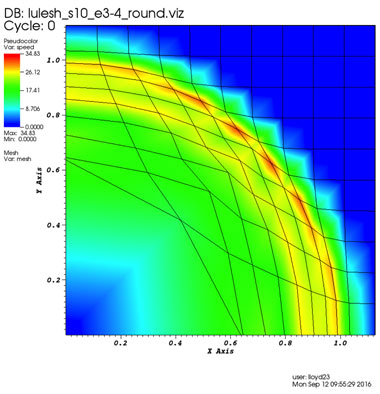
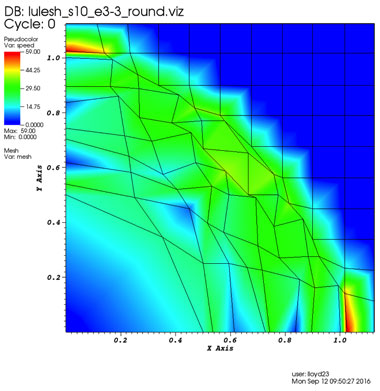
In Figure 1, we show a visualized result of running the original Livermore LULESH proxy application with double precision. For comparison, we show the same computation with unums in Figure 2. This result also gives a visual sense that unums are actually working and comparable to IEEE floating-point numbers. In contrast, in Figure 3, we show what a result looks like when precision is too low.
In the following subsections, we evaluate the results for various unum environments (i.e. different unum number sizes) in detail and compare the results with IEEE floating-point computations.
Round (Guess) After Each Operation—No Intervals
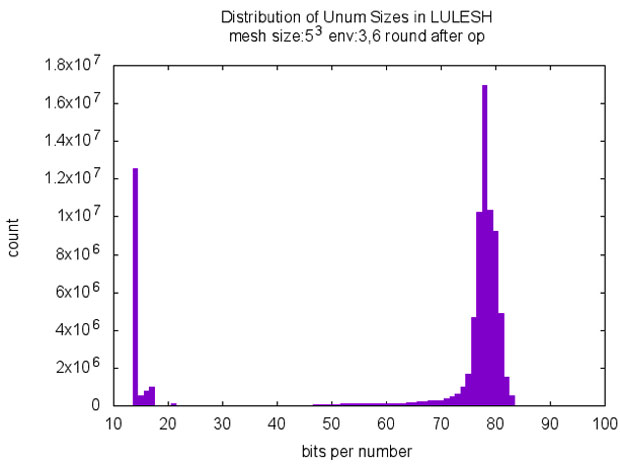
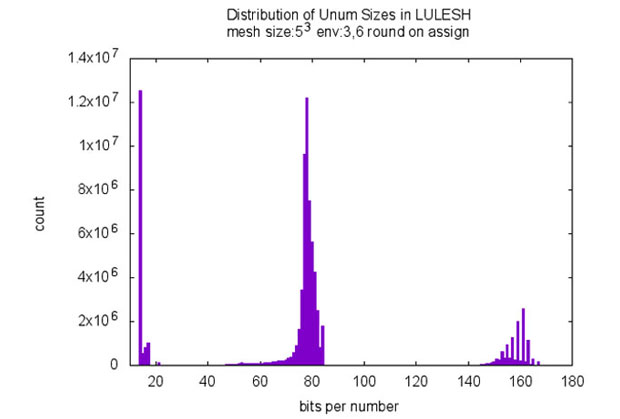
For the first modification, where we round by using the unum guess function after each operation (e.g., addition, multiply, assignment, etc.) we get promising results when comparing unums with double and long-double. In Table 1, the results are shown for different unum environments (corresponding to different unum sizes). The histogram in Fig. 4 illustrates the total number of unums computed for a run of LULESH, with the total number of unums for each unum size shown in bits.
The environment setting defines the maximum size of the mantissa and fraction of a unum. For example with an environment 3,5 we can have up to 23 exponent bits and up to 25 fraction bits. Unums allow us to perform variable precision computing, meaning we can lower the number of bits for some numbers when the unum format allows us to encode them in a more compact way. In Figure 4 we see spikes at 14-18 (which represent the numbers 0,1,2,3) and another spike at around 80 which is close to the maximum size (utilizing maximum precision). The combination of variable precise numbers allows to bring down the average number of bits used in a computation – this is shown in Table 1 in column 2 as Average Bits per Number.
The aforementioned promising result in Table 1 can be seen for environment 3,6 in comparison to double and long-double. From the table we can see savings by not storing trailing zeros and by shrinking exponent and fraction fields in the unum in the computation. In this first (of three) modes we round (unum guess) after each operation, consequently every number is represented as an exact single unum – therefore we have 100% in the column Exact (Operations Result Type), 0 % inexact (the inexact bit is never set), and 0% Pairs of unums (so called ubounds). For this run, which requires minimum changes to the code and can be selected by a single option in the code now, we get the savings in required bits for the following cases:
- LULESH with env 3,6 in comparison to IEEE double: 2 more bits on average gives between 3 and 4 decimals more accuracy with unums.
- LULESH with env 3,6 in comparison to IEEE long-double: fewer bits by a factor of 66/80 (14 bits less in unum representation on average) gives about the same accuracy (5.28E-018 vs 3.21E-018 (smaller is better)).
Table 1. Round (guess) after each operation. No intervals. LULESH statistics, problem size 53
| table 116-fs-001 | Bits per Number | Energy Differential | Operation Result Type | ||||||
| Average | Max One | Max Pair | Max Abs | Total Abs | Max Rel | Exact | Inexact | Pair | |
| env 3,2 | Time step increment too small. Need more precision. Delta time: 4.96e-05 at time step 11 | ||||||||
| env 3,3 | 16.6 69% | 24 | 49 | 36 | 80 | 4.88E-002 | 100.00% | 0.00% | 0.00% |
| env 3,4 | 24.0 73% | 33 | 67 | 6.25E-002 | 1.74E-001 | 2.47E-003 | 100.00% | 0.00% | 0.00% |
| float | 32 | 32 | N/A | 3.66E-004 | 1.08E-003 | 1.69E-006 | 100.00% | N/A | N/A |
| env 3,5 | 38.6 77% | 50 | 101 | 1.91E-006 | 2.90E-006 | 1.84E-008 | 100.00% | 0.00% | 0.00% |
| double | 64 | 64 | N/A | 2.27E-013 | 7.46E-013 | 1.72E-014 | 100.00% | N/A | N/A |
| env 3,6 | 65.7 79% | 83 | 167 | 2.22E-016 | 4.71E-016 | 5.28E-018 | 100.00% | 0.00% | 0.00% |
| long dbl | 80 | 80 | N/A | 7.77E-016 | 1.47E-015 | 3.21E-018 | 100.00% | N/A | N/A |
| env 3,7 | 118.7 80% | 148 | 297 | 9.03E-036 | 2.57E-035 | 1.74E-037 | 100.00% | 0.00% | 0.00% |
Round (Guess) on Each Assignment—All Expressions Are Calculated with Intervals
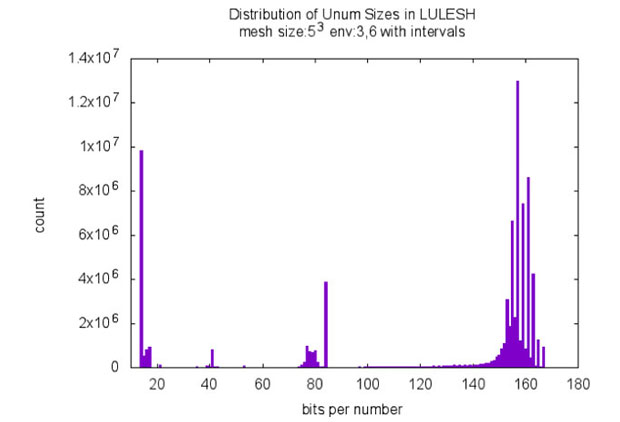
In Table 2 and Figure 5 we show the same evaluation as in Table 1 and Figure 4, but for a mode where we round only on each assignment instead of rounding after every operation. Now we compute also ubounds—pairs of unums to represent intervals—during the computation of an expression, but round them to an exact unum number. Therefore Table 2 shows a certain percentage of computed inexact and pairs (ubounds) as Operation Result Type.
Again, we see promising results when we compare the unum computation with IEEE double and IEEE long-double:
- LULESH with env 3,6 in comparison to IEEE double: 13 more bits give an additional 5 bits accuracy with unums.
- LULESH with env 3,6 in comparison to IEEE long-double: 3 less bits give us close to another decimal of accuracy with unums.
Table 2. Round (guess) on each assignment. All expressions are calculated with intervals. LULESH statistics, problem size 53
| Precision | Bits per Number | Energy Differential | Operation Result Type | ||||||
| Average | Max One | Max Pair | Max Abs | Total Abs | Max Rel | Exact | Inexact | Pair | |
| env 3,2 | Time step increment too small. Need more precision. Delta time: 5.72e-05 at time step 10 | ||||||||
| env 3,3 | 18.4 77% | 24 | 49 | 44 | 121.5 | 1.42 | 64.80% | 23.30% | 11.90% |
| env 3,4 | 27.6 84% | 33 | 67 | 1.02E-001 | 3.41E-001 | 1.35E-004 | 55.20% | 28.50% | 16.30% |
| float | 32 | 32 | N/A | 3.66E-004 | 1.08E-003 | 1.69E-006 | 100.00% | N/A | N/A |
| env 3,5 | 45.2 90% | 50 | 101 | 7.15E-007 | 2.87E-006 | 6.06E-009 | 47.60% | 33.00% | 19.40% |
| double | 64 | 64 | N/A | 2.27E-013 | 7.46E-013 | 1.72E-014 | 100.00% | N/A | N/A |
| env 3,6 | 77.2 93% | 83 | 167 | 1.80E-016 | 5.30E-016 | 9.54E-019 | 46.20% | 34.20% | 19.60% |
| long dbl | 80 | 80 | N/A | 7.77E-016 | 1.47E-015 | 3.21E-018 | 100.00% | N/A | N/A |
| env 3,7 | 139.3 94% | 148 | 297 | 2.41E-035 | 4.81E-035 | 3.26E-038 | 46.20% | 34.20% | 19.60% |
Round (Guess) Selective—Manually Adapted
In Table 3 and Figure 6 we show the same evaluation as in Table 2 and Figure 5, but for a mode where we manually defined locations in the LULESH code where we round by applying the unum guess function. The locations where selected in a systematic way by choosing assignments only to the LULESH "volume" and "time" variables and some additional cases in return statements. This amounts to about only 30 locations in the entire LULESH code that were necessary to run LULESH with unums. However, the results do not show the same impressive savings as for the previous two modes, so we consider this a work-in-progress. The promising result here is that we can actually run LULESH with such few modifications for almost all environments. Further discussions with the developers of LULESH also showed that assignments to the "time" variable could be improved by possibly clipping to the minimum of unum intervals as this would still give us correct semantics. From this we also see that domain knowledge, similar to adaptions for IEEE floats in code, can give better results, but with a variable precision and size of the number representation in unums.
We were even able to bring down the number of code modifications to only three locations in the LULESH code, but more work and insight are required to better bound lower precision environments which ran into failing checks in LULESH. However it is clear that, with a better understanding of unums, one can actually adapt code to unums with only a few changes, get results of similar accuracy with fewer bits, and explore the computation’s behavior with various levels of precision and size requirements for numbers.
Table 3. Round (guess) select expressions. Only time and volume expressions are rounded, all others are calculated with intervals. LULESH statistics, problem size 53
| Precision | Bits per Number | Energy Differential | Operation Result Type | ||||||
| Average | Max One | Max Pair | Max Abs | Total Abs | Max Rel | Exact | Inexact | Pair | |
| env 3,2 | Time step increment too small. Need more precision. Delta time: 2.86e-05 at time step 4 | ||||||||
| env 3,3 | Extreme value encountered (6.78e+38,Inf) at time step 22 | ||||||||
| env 3,4 | Extreme value encountered (6.81e+38,Inf) at time step 35 | ||||||||
| float | 32 | 32 | N/A | 3.66E-004 | 1.08E-003 | 1.69E-006 | 100.00% | N/A | N/A |
| env 3,5 | 73.4 147% | 50 | 101 | 11.8 | 12.6 | 2.15E-002 | 11.50% | 7.40% | 81.10% |
| double | 64 | 64 | N/A | 2.27E-013 | 7.46E-013 | 1.72E-014 | 100.00% | N/A | N/A |
| env 3,6 | 125 151% | 83 | 167 | 1.59E-011 | 1.65E-011 | 1.62E-014 | 11.50% | 7.40% | 81.10% |
| long dbl | 80 | 80 | N/A | 7.77E-016 | 1.47E-015 | 3.21E-018 | 100.00% | N/A | N/A |
| env 3,7 | 228 154% | 148 | 297 | 8.72E-031 | 9.04E-031 | 8.88E-034 | 11.60% | 7.30% | 81.10% |
Indexing Support for Variable Length Unum Representation
Unums as a representation can be supported using a fixed-length representation, however the full concept includes the length variability to vary the precision dynamically (on demand as needed).1 A frequent initial criticism is that unums do not match well with high-performance computing applications' use of indexing. If in the variable length format unums are expensive to randomly index, it could be a significant barrier to adoption; at least for the variable length unum form. Thus, we were especially interested in including this issue in our study.Organization of Data
Data within high-performance computing computations are frequently represented in arrays of data structures or data structures of arrays, and without loss of generality, we can assume either and present the simplification to a single array representation. For fixed-length floating-point representation, individual elements of the array can be selected using explicit indexing, a concept widely supported across most general purpose languages, such as C, C++, and Fortran.
With this fixed-length format, the address calculation can be trivially done to support the explicit look-up of index elements of the array by using the index value, the length of the element, and the base address of the array. In contrast, the support for a variable-length floating-point format would not be as easily done and would be expensive, requiring an iteration over the length of the array data to the index value, that is, an explicit search O(n) instead of a look-up using address arithmetic O(1).
Indexing Requirements for High-Performance Computing Applications
For applications that truly require random access to data, the use of this variable length form of unums may be a significant issue without a dynamically generated indirection table. The generation and use of such an indirection table to point into specific unum entries would be both cumbersome and expensive to support.
However, a broad class of computations within high-performance computing does not require random access operations into data and these might be quite suitable for use with the unum variable length format. Some operations sweep over large multidimensional arrays of data and are most commonly expressed in code using random access indexing operations. This broad class of computations would appear to be a problem for a unum variable-length format and can be canonically represented by stencil operations on large multi-dimensional data sets.
An example of a common stencil operation for local averaging operation as code is as follows:
for (i=0; i ¡ n; i++)
for (j=0; j ¡ n; j++)
a[i][j] = (b[i+1][j] + b[i-1][j]
+ b[i][j+1] + b[i][j-1]) * 0.25;
The code is expressed using explicit indexing that can be used to support random accesses of data. However the array accesses are a well defined pattern that is statically analyzable and need not be expressed using explicit array indexing. Because it is statically analyzable it can be rewritten, either by the user or by a compiler, to be expressed as a streaming operation.
An example of the previous code fragment using streaming operations is as follows:
In this case, we have used array abstractions to define the equivalent array operations. There are many forms of this across different languages (e.g., array class libraries in C++, Fortran 90 array abstractions, etc.). The proliferation of array languages in the 1980s provides a large number of examples of this concept used to express equivalent operations without the explicit requirements of indexing.
As a streaming operation, instead of an explicit indexing operation, it is easier to see how one can provide support for variable-length unums.
Variable Length Unum Support using Streaming Operations
Where high-performance computing operations can be expressed as streaming operations, the full stream is processed implicitly. Since all values are visited, the need to index specific values is replaced by the requirement to recognize them as they are accessed in-order within the streaming operation. Thus what would be the linear search to access an indexed element of the variable length unum array is folded into the evaluation of the streaming operation. The decoding of individual starting locations of fixed parts of the stream (the stencil starting array references, e.g., b(I - 1,J) would only have to be recognized—a simple counting operation. Once all starting array references were recognized, operations on the array elements would be similar to classical strip mining operations to support vector operations. The variable length feature would have to be supported though pipeline decoding, not too different in functionality to pre-fetch operations. In this way unum computing on variable length format representations could be similar to classical vector operations on older vector machines (long vector length hardware support, not more modern SIM card vector operations).
Compiler Transformations
Compiler transformations to support the conversion of identifiable stencil operations to streaming operations are possible and the subject of prior work on stencil compilers generally and specific stencil domain-specific-language support by the ROSE team at Livermore. The source-to-source compiler approach is especially well suited to this since it leverages any vendor compiler for additional back-end optimizations.
Impact on Mission
Our work, with its focus on the fundamentals of floating-point handling within the high-performance computing environment, directly addresses the Laboratory's high-performance computing, simulation, and data science core competency. In addition, the project further enables this core competency by addressing the hardware, compiler, language, and analysis concerns in the context of Laboratory applications.
Conclusion
In regard to unums obeying the associative law, they will not necessarily give exactly the same answer with a different computation order; however, the result will still be correct. This is what John Gustafson calls obeying the “sub-associative law.”1 Even though the resulting intervals are not exactly the same, both intervals will contain the correct answer. A similar claim for unums is made for obeying the “sub-distributive law”. Fused operations must be done in the g-layer for operations on unums to be “fully” associative or distributive.
What can be done better with unum intervals than with IEEE floats? The description of the Boost interval library outlines several reasons that an interval library may be useful:2
- When the input data has some built-in imprecision, use an interval instead of a number for the input variable.
- When solving equations, bisect an interval until the interval width is small enough.
- When rendering computer graphics images, reduce computations with boxes, segments, or rays to computations with intervals.
- When computations do not produce exact results, use intervals to quantify the propagation of rounding errors.
We investigated three variants (1) rounding after each operation, (2) rounding after each assignment, and (3) manually placing rounding functions (the unum guess function) in the LULESH code. LULESH ran successfully with unums using automatic rounding in these three modes. Our results also indicated the following:
- Little change was required to the source code.
- Unum environments could be set from the command line.
- Unums could help in finding the needed precision for an application.
- Variable length encoding could reduce bits moved by 10–20.
- Better accuracy (based on symmetry) was obtained for a given number of bits.
Our evaluation also showed that even when starting with a program written for IEEE floating-point, one can incrementally convert it into a program using unums only. We obtained promising results for unums in comparison to double and long-double of reduced average bits requirements for LULESH. Further work is required to obtain conclusions on how to utilize the full semantic power of unums with respect to correctness and imprecision without the unum guess function. However, it is clear that many of the recent, on-going discussions of unums versus floating-point computations are fueled by pros and cons of unums and floating-point representations and that unums are a major contribution to variable precision computing.
In future work, the unum library could be used as an analytical tool to explore the potential benefits of variable precision computing in other applications besides LULESH. The controls and feedback provided by the unum environment can be used to adjust the precision to the size needed for an entire application or for individual subcomponents. Three modes of control—manual, guided, and auto—could be used to set the precision. Manual mode relies on the user to specify the precision and make the decision between accuracy and storage space. In guided mode, an information-per-bit ratio or other metric is given as guidance to the unum environment and then the unum implementation makes the final decision on the precision. Auto mode requires exploring a range of precision settings with feedback from the application to reach a desired accuracy or performance goal. Other considerations for future work include:
- Exploring operations on unum vectors that are bit packed.
- Investigating using an alternate format for unums that would use standard IEEE data types (half, single, or double-precision) and a byte or two of metadata to encode the precision and the interval. The new format would give the mathematical properties of unums, but use standard data types addressable by current machines.
- Improving the performance of the current unum library by implementing operations with IEEE floating-point hardware. Special attention to setting the rounding mode would be necessary, but could provide relatively fast operations on numbers up to 80-bits on an x86 platform.
References
- Gustafson, J. L., The End of Error: Unum Computing. Chapman and Hall/CRC Computational Science, Boca Raton, FL (2015).
- Melquiond, G., "Boost interval arithmetic library." Boost C++ Libraries. (2006). http://www.boost.org/doc/libs/1_61_0/libs/numeric/interval/doc/interval.htm