1. Home
  2. Report Archives
  3. FY2015 LDRD Annual Report
  4. Nuclear, Chemical, and Isotopic Science and Technology
  5. Why Is Nuclear Matter So Red?

Why Is Nuclear Matter So Red?

Darren Bleuel (13-LW-003)

Abstract

An unexplained low-energy enhancement in the radiative strength function of some nuclei was experimentally researched to uncover its nature and suggest a theoretical explanation. We discovered this function to be dipole in nature without a discernible trend with mass number as previously observed. Furthermore, work on this project has led to additional measurements to determine the electric versus magnetic nature of the enhancement. While its microscopic origin remains a mystery, recent accurate measurements of the function and nuclear level densities have been used in Hauser–Feshbach nuclear reaction theory codes, producing a remarkably predictive capability to theoretically calculate neutron capture cross sections.

Background and Research Objectives

The radiative strength function represents the ability of nuclear matter to absorb and emit photons of a given frequency. The radiative strength function, together with the nuclear-level density and the nuclear optical model, controls the rate of neutron captures responsible for formation of elements heavier than iron in stellar cores and supernovae explosions. At high energies, the radiative strength function is dominated by a collective oscillation of the protons against the neutrons called the giant dipole resonance. However, there has long been a significant uncertainty in the radiative strength function at the lower “redder” energies (≤1 MeV) found in the astrophysical settings where the elements are formed because of the lack of a good experimental probe. The low-energy radiative strength function is extracted from measurements of the quasi-continuum radiation emitted by an excited nucleus. In 2001, the Livermore group performed two experiments using particle-gamma spectroscopy with silicon and sodium iodide detectors, indicating the presence of a strong enhancement in the radiative strength function at low energies in iron and molybdenum nuclei.1–3 The nuclear science community greeted this result with significant skepticism because of the lack of any known theoretical mechanism for the enhancement and the fact that a measurement of the radiative strength function in the same nucleus using the other main quasi-continuum detection technique showed no evidence of a low-energy enhancement.4,5 However, because both approaches have significant systematic uncertainties, the existence of the enhancement remained highly contentious in the intervening decade.

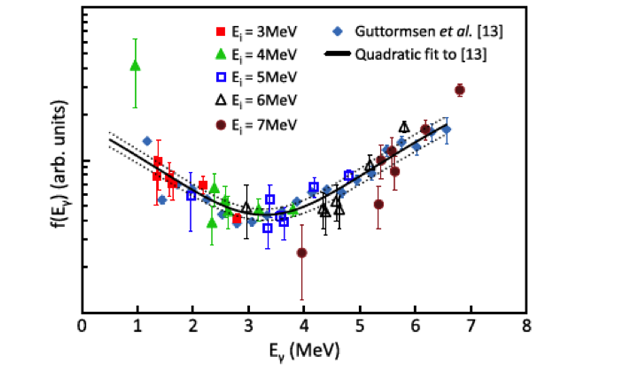
In 2012, the Livermore group, which started the debate, developed the Wiedeking method, a new way of determining the low-energy radiative strength function that is free of the systematic uncertainties of the other methods,6 unambiguously confirming the existence of the low-energy enhancement in molybdenum-95, shown in Figure 1. While this result proved that the enhancement exists, its nature and extent remained a mystery.

Figure 1. agreement of the radiative strength function in molybdenum-95 when measured by the oslo method (blue triangles) and the wiedeking method (other data points). the enhancement at low energies (<3 mev) is apparent.
Figure 1. Agreement of the radiative strength function in molybdenum-95 when measured by the Oslo Method (blue triangles) and the Wiedeking method (other data points). The enhancement at low energies (<3 MeV) is apparent.

 

In collaboration with the University of Oslo group and iThemba Laboratory for Accelerator Based Sciences in South Africa (and later Ohio University and Lawrence Berkeley National Laboratory), we performed a number of radiative strength function and nuclear-level density measurements to systematically define the mass region over which the enhancement exists. We also sought to uncover properties of the enhancement, such as the multipolarity and electromagnetic nature, to hypothesize and test possible theories as to the origin of the enhancement.

Through the course of this project, we made a number of important new discoveries which added to our research objectives. First, we discovered a “scissors mode” resonance at 2 to 4 MeV in all actinides thus far measured. As a result, we embarked on a campaign to provide actinide targets to the University of Oslo to comprehensively study as many nuclei in this region as possible, through and beyond the project period. Second, we discovered that (n,γ) cross sections can be predicted with remarkable accuracy by inclusion of our measured radiative strength function and nuclear-level density data into Hauser–Feshbach nuclear reactions codes, especially the unpredicted perturbations such as the aforementioned scissors-mode resonance or the enhancement. Finally, in preparation for emerging worldwide unstable beam capabilities, we have developed new methods for studying neutron-rich nuclei, including the “beta-Oslo” method and inverse kinematic techniques. We also strove to test fundamental assumptions, such as the independence of the strength function to excitation energy and angular momentum, by repeating previous measurements in new energy and angular momentum regimes.

Scientific Approach and Accomplishments

A variety of techniques can be used to measure the radiative strength function and nuclear-level density of a nucleus. The Oslo method was developed and primarily conducted at the Oslo Cyclotron Laboratory at the Center for Accelerator-based Research and Energy Physics at the University of Oslo.7 Charged particle reactions produce nuclei in excited states below the neutron separation energy, which then decay by gamma emission. At each excitation energy, the first-generation gamma spectrum is determined from particle–gamma coincidence data through an iterative sequential subtraction technique. This spectrum represents the overall probability of gamma decay, proportional to the product of the radiative strength function and the nuclear-level density. Predicted by Fermi’s Golden Rule and the Brink–Axel hypothesis (which asserts that the radiative strength function depends only on the energy of the emitted ray), the nuclear-level density and radiative strength function contributions can be separated by a fit to the first-emission spectra at all the excitation energies, assuming the radiative strength function is independent of excitation energy.

Complementary to the Oslo method, the Wiedeking method also employs similar charged particle beams to determine the radiative strength function below particle-separation energies.6 Similar to the Oslo method, an outgoing charged particle is measured using silicon detectors to determine the excitation energy of the nucleus. However, high-resolution, high-purity germanium detectors are used rather than sodium iodide detectors to detect gamma rays. Then, only events where two gamma rays are detected with a sum energy equal to the excitation energy are selected. The first-emitted gamma ray is determined by gating on a gamma ray connecting known discrete low-lying energy levels in the nucleus of interest. A relative radiative strength function can be generated for a given known discrete state by varying the excitation energy.

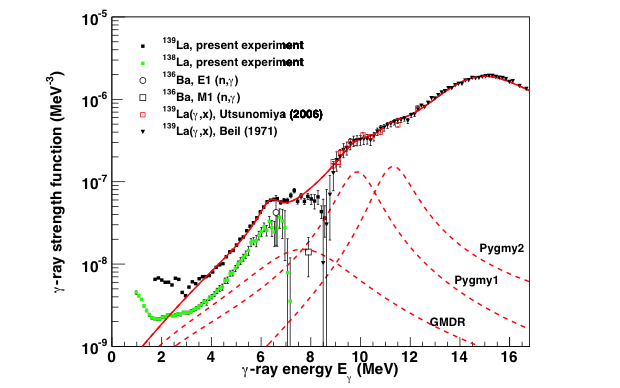
Through our continuing experiments at the University of Oslo, Lawrence Berkeley National Laboratory, Ohio University, and iThemba Laboratory over the past two decades, we and our collaborators have measured the radiative strength function and nuclear-level density of almost a hundred different nuclei using both methods. Over the course of this project, we have focused on exploring the nature, scope, and influence of the low-energy enhancement. It was previously thought that the enhancement did not exist in medium-mass nuclei (atomic mass number of ~100 to ~200). But through this systematic study, we have discovered the enhancement in lanthanum nuclei shown in Figure 2 and its absence or suppression in several actinides,8 suggesting a more nuanced dependence on the proton and neutron number.

Figure 2. preliminary measured radiative strength function of lanthum-138 and -139, showing a low-energy enhancement.
Figure 2. Preliminary measured radiative strength function of lanthanum-138 and lanthanum-139, showing a low-energy enhancement.

 

We also launched a multi-institutional campaign to study the nucleus for germanium-74, using as many known approaches as possible to ensure that the experimental method does not bias the results. Good agreement has thus far been shown between three different experimental methods.9,10

Our collaborators at the University of Oslo recently showed that the low-energy enhancement in iron-56 is dipole in nature.11 A number of theories have recently been proposed to explain the enhancement as either an electric dipole or a magnetic dipole.12–14 Measuring the electromagnetic properties of gamma rays emitted at low energy in nuclei exhibiting the enhancement is therefore crucial to identifying the most appropriate theory. To this end, we designed and conducted an experiment at Argonne National Laboratory to measure this property through the angular distribution of Compton-scattered secondary photons in the Gretina high-purity germanium gamma-ray tracking array. This data is currently being analyzed by our collaborators at Lawrence Berkeley National Laboratory, extending our research discoveries beyond the short term of this project.

Furthermore, we performed an experiment at the LICORNE facility in Orsay, France, to test the Brink–Axel hypothesis itself (LICORNE is a high-flux, directional neutron source based at the tandem accelerator of the Institute of Nuclear Physics, University of Paris, Orsay). Using the Miniball germanium detector array, we repeated a radiative strength function measurement using a two-step cascade technique5 following 95Mo(n,γ)96Mo reactions, but at higher energy (~1.5 MeV) than the original thermal experiment, thereby populating a broader range of states and angular momenta. If the results do not match the previous results from thermal neutron absorption, it would suggest a nuclear-state dependence on the radiative strength function and that the Brink–Axel hypothesis may not be robust.

Following the discovery of a scissors resonance in the radiative strength function of several actinides, and its importance to accurate theoretical predictions of (n,γ) cross sections in this region, we embarked on a campaign to provide targets using the unique actinide target-making capabilities of LLNL. We first constructed plutonium-239 and -242 targets to study dependence of the resonances on neutron number. We have also made neptunium-237, plutonium-240, and an extremely rare plutonium-244 target that is being delivered to the University of Oslo for experiments after the completion of this project, further mapping out the parameter space of neutron and proton number in the actinide region. Thus far, the low-energy enhancement has been observed in some but not all actinides, suggesting further a theoretical explanation based on selective particle-orbital transitions.

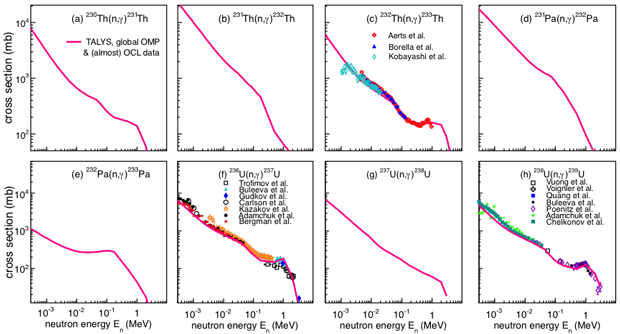
Finally, theoretical work has started to input these radiative strength function and nuclear-level density measurements into Hauser–Feshbach codes, such as TALYS, to predict (n,γ) cross sections. The first such calculation on actinides, shown in Figure 3, demonstrated a remarkable agreement with experimental measurements where such measurements existed, along with new predictions of many cross sections in this region that are extremely difficult or impossible to measure directly.

Nd livermore’s neural tech group are
Figure 3. Theoretical predictions of (n,γ) cross sections in several actinides (lines) compared with experimental data, when known (data points).

 

Accomplishments

In addition to shedding new light on the fundamental science question first posed, this research has proven a new, potentially more accurate technique for predicting nuclear reaction cross sections that cannot be measured directly. This technique has been introduced as a new tool for existing programs. Development of the beta-Oslo technique led to a new research project to begin a long-range LLNL program at the Facility for Rare Isotope Beams. The first experimental proposal, to determine the (n,γ) cross section of a short-lived fission fragment (important to interpretation of fission-fragment mass distributions in test program samples), has already been accepted at the National Superconducting Cyclotron Laboratory, the precursor to the Facility for Rare Isotope Beams. We have partnered with the University of Oslo, iThemba Laboratory, University of California, Ohio University, and Lawrence Berkeley National Laboratory to analyze data sets from experiments we performed and to conduct experiments with actinide and other targets supplied by this project. Lastly, our research was influential in the approval of a new Coordinated Research Project under the auspices of the International Atomic Energy Agency to compile the first-ever evaluated data base of radiative strength functions for use in reaction-rate calculations.

Impact on Mission

Our work in determining the nature of low-energy enhancement in the radiative strength function can significantly improve understanding of the properties of nuclear matter and nucleon–nucleon interactions. Important applications include weapon aging, Inertial Confinement Fusion, and neutron-capture experiments in support of Laboratory missions in stockpile stewardship science and energy security, as well as the core competencies in nuclear, chemical, and isotopic science and technology and high-energy-density science.

Conclusion

We have completed an extensive campaign focused on revealing the nature of and explaining the unexpected low-energy enhancement discovered in the radiative strength function of certain nuclei. Over the short course of this project, we have completed the necessary experiments to probe the properties of the enhancement, develop theories for its existence, and established the collaborations necessary to fully analyze the results and continue the research. A prevailing theory fitting the current observations, remaining to be confirmed by our collaborators’ analyses, appears to be that the enhancement is due to M1 transitions between specific, similar particle orbitals. Several newly funded projects, including work for the NNSA Nuclear Science and Security Consortium, as well as Laboratory programmatic support, will allow us to continue LLNL’s leadership in this field.

References

  1. Voinov, A., et al., “Large enhancement of radiative strength for soft transitions in the quasi continuum.” Phys. Rev. Lett. 93, 142504 (2004).
  2. Guttormsen, M., et al., “Radiative strength functions in 93-98Mo.” Phys. Rev. C 71, 044307 (2005).
  3. Larsen, A. C., et al., “Nuclear level densities and γ-ray strength functions in 44,45Sc.” Phys. Rev. C 76, 044303 (2007).
  4. Sheets S. A., et al., "Test of the statistical model in 96Mo with the BaF2γ calorimeter DANCE array." Phys. Rev. C 79 024301 (2009).
  5. Krtička, M., et al., “Two-step γ cascades following thermal neutron capture in 95Mo.” Phys. Rev. C 77, 054319 (2008).
  6. Wiedeking, M., et al., “Low-Energy Enhancement in the Photon Strength of 95Mo.” Phys. Rev. Lett. 108, 162503 (2012).
  7. Schiller, A., et al., “Extraction of level density and γ strength function from primary γ spectra.” Nucl. Instrum. Methods Phys. Res. A 447, 498 (2000).
  8. Guttormsen, M., et. al., “Scissors resonance in the quasicontinuum of Th, Pa, and U isotopes.” Phys. Rev. C, 89, 014302 (2014).
  9. Renstrøm, T., et. al., “First evidence of low energy enhancement in Ge isotopes,” EPJ Web Conf. 93, 04003 (2015). LLNL-CONF-678765.
  10. Massarczyk, R., et al., “Dipole strength distribution of 74Ge.” Phys. Rev. C 92, 044309 (2015).
  11. Larsen, A. C., et al., “Evidence for the dipole nature of the low-energy γ enhancement in 56Fe.” Phys. Rev. Lett. 111, 242504 (2013).
  12. Litvinova E., and N. Belov, “Low-energy limit of the radiative dipole strength in nuclei.” Phys. Rev. C 88, 031302(R) (2013).
  13. Schwengner, R., S. Frauendorf, and A. C. Larsen, “Low-energy enhancement of magnetic dipole radiation.” Phys. Rev. Lett. 111, 232504 (2013).
  14. Brown, B. A., and A. C. Larsen, "Large low-energy M1 strength for 56,57Fe within the nuclear shell model." Phys. Rev. Lett. 113, 252502 (2014).

Publications and Presentations

  • Giacoppo, F., et al., "Level densities and thermodynamical properties of Pt and Au isotopes." Phys. Rev. C 90, 054330 (2015). LLNL-JRNL-664179.
  • Giacoppo, F., et al., "γ decay from the quasicontinuum of Au197,198." Phys. Rev. C 91, 054327 (2015). LLNL-JRNL-678760. http://dx.doi.org/10.1103/PhysRevC.91.054327
  • Guttormsen, M., et al., “Constant-temperature level densities in the quasicontinuum of Th and U isotopes.” Phys. Rev. C 88, 024307 (2013). LLNL-JRNL-645275.
  • Guttormsen, M., et. al., Experimental level densities of atomic nuclei. (2015). LLNL-JRNL-678650.
  • Guttormsen, M., et al., “Observation of large orbital scissors strength in actinides.” Acta Phys. Pol. B 44, 567 (2013). LLNL-JRNL-645274.
  • Guttormsen, M., et al., “Observation of large scissors resonance strength in actinides.” Phys. Rev. Lett. 109, 162503 (2013). LLNL-JRNL-582232.
  • Guttormsen, M., et al., “Scissors resonance in the quasicontinuum of Th, Pa, and U isotopes.” Phys. Rev. C 89, 014302 (2014). LLNL-JRNL-664178.
  • Larsen, A. C., et. al., Experimentally constrained (p,γ)89Y and (n,γ)89Y reaction rates relevant to the p-process nucleosynthesis. (2015). LLNL-JRNL-678709.
  • Laplace, A., et. al., Statistical properties of 243Pu and 242Pu(n,γ) cross section calculation. (2015). LLNL-JRNL-678708.
  • Larsen, A. C., et al., "Upbend and M1 scissors mode in neutron-rich nuclei—consequences for r-process (n,gamma) reaction rates." Acta Phys. Pol. B. 46(3), 509 (2015). LLNL-JRNL-678761. http://dx.doi.org/10.5506/APhysPolB.46.509
  • Liddick, N., et. al., Exotic nuclear reactions and the heavy element nucleosynthesis puzzle. (2015). LLNL-JRNL-678694.
  • Renstrøm , T., et al., "First evidence of low energy enhancement in Ge isotopes." EPJ Web Conf. 93, 04003. (2015). LLNL-CONF-678765. doi:10.1051/epjconf/20159304003
  • Renstrøm, T., et. al., Low-energy enhancement in the γ-ray strength functions of 73,74Ge. (2015). LLNL-JRNL-678756.
  • Wiedeking, M., et. al., Gamma-ray decay from neutron-bound and unbound states in 95Mo and a novel technique for spin determination. (2015). LLNL-JRNL-678755.