Ogden S. Jones (15-ERD-058)
Abstract
Previous indirect-drive Inertial Confinement Fusion experiments have mostly used cylindrical, laser-heated, gas-filled hohlraums to produce the radiation drive needed to symmetrically implode deuterium–tritium-filled fusion capsules. To date, these hohlraums have been unable to produce a symmetric radiation drive through the end of the desired drive pulse, and are plagued with complications due to laser–plasma interactions that have made it difficult to predict their performance. We explored several alternate hohlraum design concepts that utilize different geometries, radiation shields, and foam materials in an attempt to improve performance relative to cylindrical hohlraums. Each alternate design was optimized using radiation hydrodynamic design codes to implode a reference deuterium–tritium capsule with a high-density carbon ablator. The laser power and energy required to produce the desired time-dependent radiation drive and the resulting time-dependent radiation symmetry for each new concept were compared to the results obtained from a reference cylindrical hohlraum. Since several of the new designs needed extra laser entrance holes (LEHs), techniques to keep small LEHs open longer (including high-Z foam liners and low-Z wires at the hole axis) were investigated numerically.
Supporting experiments and target-fabrication efforts were also conducted at Lawrence Livermore National Laboratory's Jupiter Laser Facility as part of this project. Plastic tubes open at one end (halfraums) and filled with SiO2 or Ta2O5 foam were heated with a single two-watt laser. Laser propagation and backscatter were measured. The measured propagation generally was slower than calculated, and the measured laser backscatter was less than calculated. A comparable scaled-up experiment was designed for the Laboratory's National Ignition Facility and four targets were built. Since low-density gold foam was identified as a desirable material for lining the LEHs and the hohlraum wall, a technique was developed to produce 550-mg/cc gold foam. A sample of this material was successfully manufactured.
Background and Research Objectives
High-energy-density physics and Inertial Confinement Fusion (ICF) experiments would benefit from the development of a laser-driven hohlraum that consistently provides an efficient and spherically symmetric radiation drive without the complications of hot-electron production, non-LTE (local thermodynamic equilibrium) x-ray preheat, and the need for cross-beam energy transport (CBET). A more-energy-efficient hohlraum would enable access to desired radiation-temperature regimes within the constraints of available laser energy, while more symmetric drive would help to achieve highly converged, high-yield capsule implosions. To date the indirect-drive experiments in Lawrence Livermore National Laboratory's National Ignition Facility (NIF) have principally utilized cylindrical gas-filled target hohlraums have faced a number of challenges. At ignition-relevant powers of 300 to 500 TW and hohlraum He-fill-gas densities of 1–1.6 mg/cc, 10 to 20 percent of the laser light is backscattered out of the hohlraum (Glenzer et al. 2012). The inner-cone beams, which have a long path length through relatively cool plasma, undergo stimulated Raman scattering, preventing the proper inner-cone/outer-cone balance that is required for symmetry and generating high-energy electrons that preheat the capsule. CBET between the inner and outer beams crossing at the laser entrance hole (LEH) has proven difficult to model, requiring ad hoc adjustments (Jones et al. 2016), and therefore reducing control of hohlraum wall motion, resulting in unwanted and damaging symmetry swings. The standard practice of using gas to fill hohlraums has not been entirely successful in controlling the wall motion. In addition, the gas-filled hohlraums have suffered from a deficit in radiation drive relative to vacuum hohlraums by as much as 15 to 20 percent in absorbed energy (Jones et al. 2012). The combined backscatter and drive losses amount to as much as a 40-percent reduction in efficiency.
Some attempts were made to improve the efficiency of the standard gold gas-filled hohlraum: (1) the gold wall has been replaced by gold-lined uranium, and (2) the wall shape has been changed from a cylinder to a rugby-ball shape to reduce wall area. These improvements have helped to some degree, but major challenges remain in current hohlraum modeling techniques. The primary goal of this project was to redesign the hohlraum to develop one or more platforms that can support long, low-adiabat laser pulses while maintaining a high degree of efficiency, symmetry, and modeling integrity for Inertial Confinement Fusion experiments. Another key application for new simplified hohlraums that don’t produce excessive electron and x-ray preheat is in high-energy-density studies (e.g., thermal and radiation transport).
The objectives of this project were to (1) develop several alternative hohlraum designs using numerical tools, (2) assess the calculated performance of these new hohlraum designs relative to a gas-filled cylindrical hohlraum, (3) develop fabrication techniques for foam fills and liners used in these new designs, and (4) conduct experiments to obtain data relevant to the most uncertain and highest risk aspects of the new hohlraums. These objectives were generally met during the course of this three-year project. Originally, three new hohlraum design concepts were proposed. During that time, two additional designs were proposed and assessed, so that ultimately five new hohlraum designs were studied. Of the five, at least two designs are under consideration for further work by the ICF Program. In the fabrication area, a technique was developed for making gold foam at 550 mg/cc and a sample of the material was fabricated successfully. In addition, foam-filled targets made from SiO2 and Ta2O5 were manufactured using existing techniques for experiments at the Laboratory's Jupiter Laser Facility (JLF) and the NIF. Experiments to measure the propagation and backscatter of a single laser beam into a foam-filled can were completed on the JLF's Janus laser.
Scientific Approach and Accomplishments
To assess the alternate hohlraum designs, we used a reference capsule-ignition design that was driven by a three-shock radiation source with a peak radiation temperature of 300 eV. The capsule consisted of a high-density carbon (HDC) ablator surrounding a cryogenic deuterium–tritium (DT) fuel layer. The HDC capsule had an outer radius of 1,108 microns, an ablator thickness of 76 microns, and a DT fuel thickness of 56 microns. The HDC ablator was doped with 0.275-percent tungsten dopant. This is a high-gain design. The capsule absorbed about 150 kJ of energy and the calculated one-dimensional yield was greater than 16 MJ.
For each of the new hohlraum designs we used the Lasnex radiation hydrodynamic code (Zimmerman and Kruer 1975) to determine the absorbed laser power versus time for each beam in the NIF required to produce the radiation drive for the reference HDC capsule while maintaining adequate radiation symmetry. The NIF has 192 laser beams arranged in groups of four, called quads. The quads are arranged in rings at eight polar angles relative to the axis of a cylindrical hohlraum (physically the vertical axis in the NIF target chamber). The polar angles for the 24 quads coming from the top half of the chamber are 23.5, 30, 44.5, and 50 degrees. The target chamber is top/bottom symmetric, so the bottom 24 quad angles are designated as 180-23.5 degrees, etc. The 23.5-degree and 30-degree beams are called the inner cones and are directed at the midplane of a cylindrical hohlraum. The 44.5-degree and 50-degree beams are called the outer cones and are directed closer to the LEHs. Two-thirds of the NIF's beams are outer-cone beams, and one third are inner-cone beams. To take full advantage of the NIF's laser power, approximately the same peak power is required for all the beams. If the inner-cone fraction is defined as the power of all the inner cones divided by the total power, that is equivalent to saying that an inner-cone fraction of 33 percent is required at peak power.
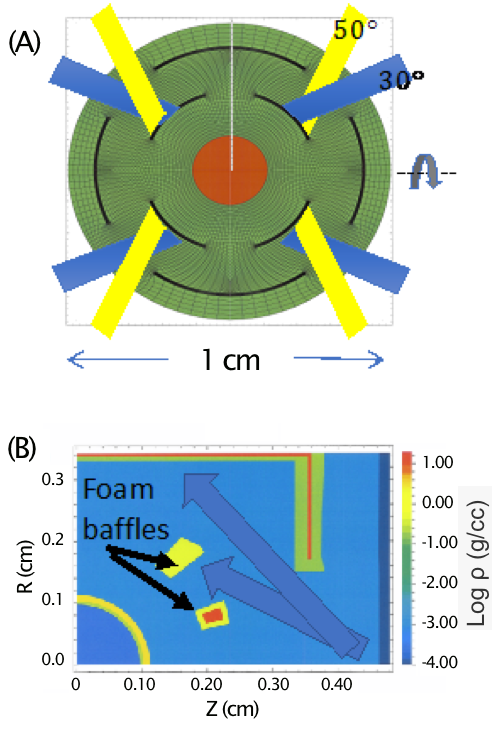
The first hohlraum that we designed was called the “ballraum,” which is shown in Figure 1A. This is a spherical hohlraum with an annular LEH on each side through which all of the beams from each side of the chamber enter. In the figure only the 30-degree and 50-degree beams are shown for clarity, but the 23.5-degree and 44.5-degree beams also enter through the same LEH.
Upon entering the hohlraum, the beams hit an annular high-Z shield that converts the laser energy to x rays. The shield size and location is used to minimize the radiation asymmetry on the capsule. The shields essentially form a secondary spherical hohlraum that shields the capsule from a direct view of the laser hot spots. All the beams have the same power, so this has the ideal 33-percent cone fraction by construction.
In the design calculations, solid-density gold was used for the outer wall and shields, although metal foams could be used as well. The NIF phase plates for the 44.5-degree beams (elliptical spot with radii of 343 and 593 microns) were used because they are much smaller than the 23.5-degree and 30-degree beam phase plates, and thus enabled use of a smaller LEH diameter. After some optimization, an outer radius of 4 mm and an inner (shield) radius of 2.5 mm were chosen. This design calculation produced a nearly symmetric ablation pressure on the capsule. The P2/P0 Legendre moment of the ablation pressure was nearly flat in time, and the time-integral of the ablation pressure was -1.5 percent. This is generally better P2 control than that calculated for cylindrical hohlraums. However, a laser pulse delivering 1.5 MJ of absorbed energy was only able to achieve a peak radiation temperature of approximately 195 eV, which was far below the 300 eV needed to drive the HDC ignition capsule. Thus, the ballraum design was not viewed as a viable candidate for an ignition hohlraum in the NIF due to its inefficient performance.
The second hohlraum design considered was the “baffleraum,” shown in Figure 1B. This is a cylindrical hohlraum with high-Z foam walls and two high-Z foam baffles positioned around the capsule and intercepting the inner cone beams. Radiation hydrodynamic calculations showed that a laser pulse with 400-TW peak power and 1.65 MJ absorbed laser energy could provide the desired 300-eV radiation drive. The cone fraction was set to the ideal 33 percent and the baffles' configurations were varied to control the radiation symmetry. A baffle placement was achieved that resulted in the P2/P0 moment of the integrated radiation flux at the capsule radius of 0, and a P4/P0 moment of -2 percent. However, there were large time-dependent swings in the radiation symmetry, and the calculated symmetry was very sensitive to small changes in the baffle size and placement. This design was not pursued farther because the symmetry would be too difficult to predict and to control.
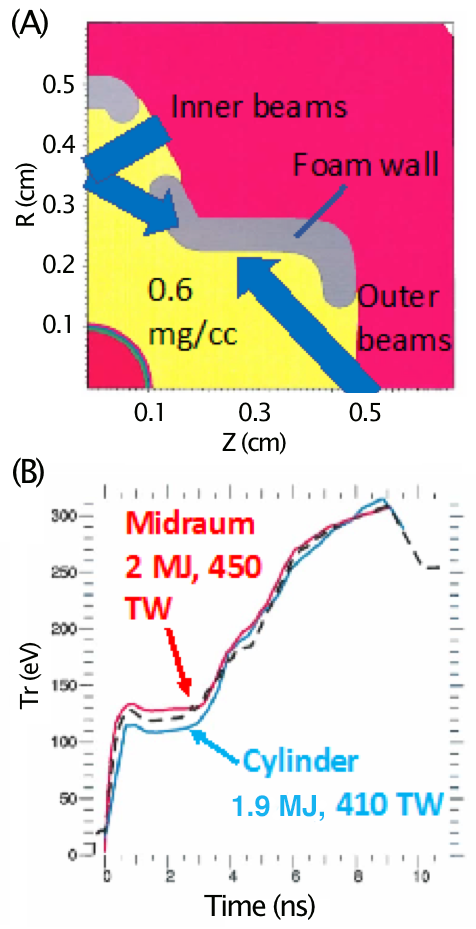
The third hohlraum design considered was the “midraum,” shown in Figure 2. In this design, the inner cone beams (blue arrow) are rerouted from the usual LEH to enter the hohlraum through eight additional LEHs located near the hohlraum midplane. This configuration eliminates the complication of CBET between the inner and outer cones, and shortens the path length for the inner-cone beams to reach the high-Z wall. In standard cylindrical hohlraums, the inner beams must propagate through the high-Z-wall plasma created by the outer beams; this interaction has led to severe difficulties in controlling the radiation symmetry late in time. By decoupling the inner and outer cones, this design eliminates that issue and has potential for increased control of radiation symmetry.
Figure 2. (A) Schematic diagram of the midraum hohlraum. (B) Graphic plot of the radiation drive produced by the midraum (red curve) and the 6.72 mm-diameter cylindrical hohlraum (cyan curve). The desired high-density carbon (HDC) ignition (Tr) is the dashed black curve.
Although each of the eight midplane LEHs accepts two inner quads (a 23.5 and a 30) in the real three-dimensional case, the midplane LEHs are treated as an annular LEH in the axisymmetric calculation shown in Figure 2a. The desired HDC ignition Tr(t) is shown (black dashed curve) in Figure 2B. We were able to match the desired drive in the midraum using a 2.0-MJ laser pulse with a peak power of 450 TW (red curve). This is comparable to the 1.9 MJ and 410 TW needed for a 6.72 mm cylindrical hohlraum (cyan curve). To make this design energetically competitive, the midplane LEHs and beams have to be small. In the calculation shown, the annular gap is 1 mm, which results in an annular LEH area of 0.253 cm2. This would lead to unacceptably large LEH losses, and we would not be able to achieve 300-eV drive. We restricted the radiation loss out of the gap so that the effective area was equal to the area of four circular LEHs of 900-micron diameter each. This has about 1/10th the area of the large annular LEH. We assumed a circular 400-micron-diameter beam spot for the inner-cone beams. Note that this is smaller than any phase plates currently available at the NIF. In order to keep the midplane LEH from closing late in time, we had to make the walls of 350-mg/cc gold foam. We were unable to achieve adequate radiation symmetry for this design with a peak cone fraction of 33 percent. However, using a non-varying 50-percent cone fraction, we obtained a value of +1.5 percent for the P2/P0 component of the radiation fluence at a radius of 0.15 cm, with almost no variation in time. Thus, this midraum design may enable improved control of radiation symmetry compared to that of a cylindrical hohlraum. However, as currently designed, it would not work well with the NIF because it needs a 50-percent cone fraction. Half of the NIF's 44.5-degree beams would have to be routed through additional LEHs at the midplane to get an effective 50-percent cone fraction.
Because the midraum concept requires a small LEH, we undertook a separate numerical study of LEH dynamics in a simple cylindrical geometry (Tabak and Jones 2017). We simulated a half-cylindrical hohlraum (“halfraum”) with a single laser beam centered on the hohlraum axis. The size and boundary conditions of the halfraum were varied to control the amount of filling in the volume due to high-Z-wall ablation because the electron density in the laser path is the critical parameter for understanding LEH dynamics. Ignoring any laser–plasma interaction issues, we found that LEHs with radii in the range of 300 to 500 microns generally could remain open to laser light through the duration of the 9-ns HDC ignition laser pulse. We also found that it was beneficial to line the wall surrounding the LEH with gold foam with a density of less than 1 g/cc and to place a CH rod at the center of the LEH to provide a source of low-Z mass to fill the LEH.
Given this result, we investigated a fourth new hohlraum design that we called the spherical hohlraum. This was a combination of the ballraum, which suffered from having too much LEH loss, and the midraum, which has more LEHs, but did not have enough drive at the waist. Each of the 48 quads in the spherical hohlraum has its own small LEH and shield to convert the light to x-rays, all of which are positioned in rings on the outside of a spherical hohlraum such that the low-mode symmetry is balanced. Calculations confirmed that it is relatively easy to get more than 300 eV in such a hohlraum. The issues will be the LEH closure, laser–plasma interaction, and the high-mode radiation asymmetry due to the radiation flowing around the 48 small shields.
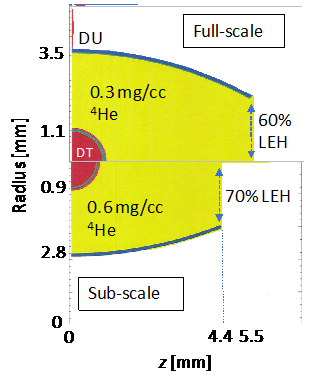
The fifth and final hohlraum design we considered was a rugby-ball-shaped hohlraum, which is shown in Figure 3. This hohlraum is not new (Amendt et al. 2014), having been shot before in the NIF, but with a high gas-fill density of 1.6 mg/cc He. The new idea here was to reduce the hohlraum fill density, shrink the hohlraum, and drive the capsule with a higher peak temperature of 330 eV.
Figure 3. Rugby-ball-shaped hohlraum with a 1,108-micron radius high-density carbon capsule (top) and 80-percent scale (sub-scale) capsule and hohlraum (bottom).
The 80-percent sub-scale capsule has a higher implosion velocity and is still a high-gain design, with about a 6-MJ one-dimensional yield. This hohlraum design only requires 1.25 MJ and 390 TW peak power to achieve the desired time-dependent radiation drive. Because the phase plates are not scaled, the intensities are the same as full scale, and the path lengths are less, resulting in lower predicted linear gains for laser backscatter instabilities. A two-dimensional calculation resulted in a yield of more than 1e17 neutrons.
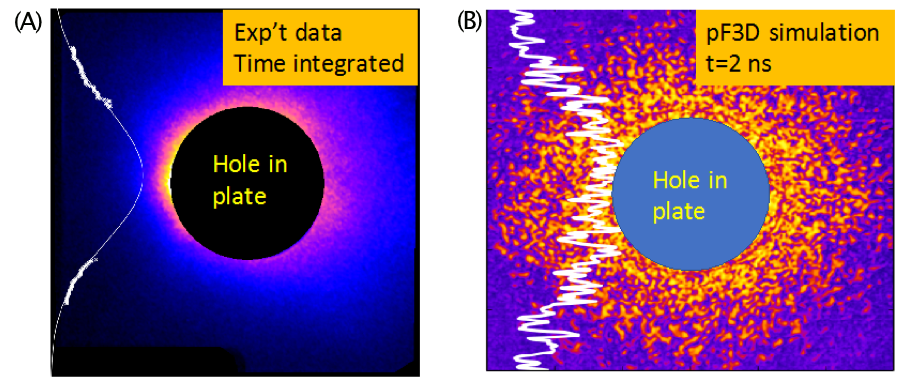
Because the midraum and the spherical hohlraum designs relied on using many small LEHs, we decided to conduct supporting experiments using a halfraum heated by a single laser beam aligned with the halfraum axis. This was essentially the geometry used in our calculations to study LEH closure. Although we ultimately wanted to measure LEH closure, we decided to begin by studying the laser interaction with a foam in a halfraum and a large LEH. The basic idea was to mock-up the geometry of a midraum inner-cone beam, which has a path length of about 2 mm and then is absorbed in the low-density gold foam, as shown in Figure 2A. The experiments were conducted at JLF. The targets were 2-mm-diameter polyimide tubes filled with either Ta2O5 foam (20 or 50 mg/cc) or SiO2 foam (2 or 5 mg/cc). The Ta2O5-filled tubes were 0.5 mm long, and the SiO2-filled tubes were 2 mm long. The tubes were backed by a gold foil. A single green laser (λ=527 nm) was configured to enter from the other (open) side and heat the foam. The laser pulse was 140 J, 2 ns long, and had a peak power of 0.1 TW. The phase plates were 200 microns in diameter, so the peak intensity was approximately 3e14 W/cm2. The primary measurements were a time-integrated, side-on x-ray image to assess the propagation of the heat front through the foam, and included a suite of diagnostics to measure the stimulated Brillouin scattering (SBS). To calculate the amount of SBS, we ran radiation hydrodynamic simulations of the experiment, created plasma maps of the temperature and electron density, and then fed these maps into the pf3d paraxial wave-equation solver (Berger et al. 1998). In general, the measured SBS was slightly less than predicted by pf3d calculations, but qualitatively, the agreement was acceptable. Some of the SBS was scattered in a cone outside the beam, hitting a plate that was imaged (Figure 4). This measurement is shown in Figure 4A. From the pf3d calculation, we made a simulated version of this measurement (shown in Figure 4B) and found that the spatial profile of the SBS on the plate was very similar to the measurement.
Since we were interested in metal foams for x-ray convertors, we supported the development of a gold foam. The foam was made by coating 10-micron polystyrene beads with gold or a gold/silver mixture. The polystyrene and the silver were chemically removed, leaving behind a low-density gold foam. The process was successfully developed and a foam with an average density of 550 mg/cc was fabricated. It is shown (magnified) in Figure 5a.
Figure 5. Photographs of (A) 550 mg/cc gold foam (magnified) and (B) a gold hohlraum target filled with Ta2O5 and SiO2.
The next step was to scale the Janus laser experiments up to the NIF facility. The targets were designed and built (see Figure 5b). They were halfraums about the same size as the Janus targets, but made of gold and they included an imaging slit. The targets were to be heated by a single NIF quad with an HDC-like pulse shape peaking at 300 TW. By using existing 400-micron-diameter phase plates and slightly defocusing the beams, the resulting peak intensity would be 2e15 W/cm2. These targets have not yet been shot in NIF.
Impact on Mission
Developing an efficient, symmetric, spectrally simpler hohlraum drive is critical for performing relevant experiments in both high-energy-density science research and stockpile stewardship. This would support more precise high-energy-density experiments that promote a better understanding of radiation flow, x-ray conversion, and self-heating burning plasmas. Research into the use of foam materials for fusion targets also aligns with the Laboratory's inertial fusion science and technology strategic focus area.
This project was the vanguard of what is now a much larger effort within the Laboratory's Inertial Confinement Fusion (ICF) Program to develop a better, more efficient hohlraum. Current and future program plans include a track for bringing “advanced hohlraums” on line to replace the cylindrical hohlraums currently in use in the NIF. These hohlraums do not look exactly like those used in this study, but they will likely share some of their more advanced features.
Conclusion
Of the five hohlraum designs that were studied, at least two will be explored further. The 330-eV rugby-ball hohlraum design has been presented to the ICF Program and they are considering whether to include it in future experiments. The midraum design concept will also be presented to the ICF Program, although in its present configuration it cannot meet the radiation-symmetry requirements. Some of the NIF's 44.5-degree beams would have to be rerouted through the midplane LEHs in order to get enough drive at the hohlraum waist, and this would require a major redesign. Finally, the four foam-filled NIF targets that were built will undergo testing for backscatter in foams at ignition-relevant power and energy levels.
References
Amendt, P., et al. 2014. "Low-Adiabat Rugby Hohlraum Experiments on the National Ignition Facility: Comparison with High-Flux Modeling and the Potential for Gas-Wall Interpenetration." Physics of Plasmas 21 (11). doi: 10.1063/1.4901195.
Berger, R. L., et al. 1998. "On the Dominant and Subdominant Behavior of Stimulated Raman and Brillouin Scattering Driven by Nonuniform Laser Beams." Physics of Plasmas 5 (12). doi: 10.1063/1.873171.
Glenzer, S. H., et al. 2012. "Cryogenic Thermonuclear Fuel Implosions on the National Ignition Facility." Physics of Plasmas 19. doi: 10.1063/1.4719686. LLNL-JRNL-523436.
Jones, O. S., et al. 2012. "A High-Resolution Integrated Model of the National Ignition Campaign Cryogenic Layered Experiments." Physics of Plasmas 19. doi: 10.1063/1.4718595. LLNL-JRNL-520495.
Jones, O. S., et al. 2016. "A New Symmetry Model for Hohlraum-Driven Capsule Implosion Experiments on the NIF." Journal of Physics Conference Series 688 (1): o12042. doi: 10.1088/1742-6596/688/1/012042.
Tabak, M. and O. S. Jones. 2017. "Initial Computational Study of a New Multi-Hole Hohlraum (the "Midraum")." doi:10.2172/1409994. LLNL-TR-741288.
Zimmerman, G. B. and W. L. Kruer. 1975. "Numerical Simulation of Laser-Initiated Fusion." Comments on Plasma Physics and Controlled Fusion 2 (2).
Publications and Presentations
Jones, O., et al. 2017. "The Advanced Hohlraum Research Project." Bulletin of the American Physical Society 62 (12). LLNL-ABS-735147.
Jones, O.S., et al. 2015. "New Advanced Hohlraums Utilizing Unique Geometries and Foam Components." Bulletin of the American Physical Society 60 (19). LLNL-ABS-675181.
Mariscal, D., et al. 2016. "Laser Backscatter and Propagation in Low-Density Ta2O5 and SiO2 Foams." Bulletin of the American Physical Society 61 (18). LLNL-ABS-697657.